Agrégation 2006 : agitation thermique d'un gaz ; énergie interne ; capacités thermiques

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

L'agitation thermique est le mouvement aléatoire des particules constituant le gaz. Ce mouvement est du à l'énergie microscopique des particules.

Définition du kelvin, unité de température thermodynamique, à partir du point triple de l'eau :

point triple de l'eau : T_T(eau) = 273,16 K ; 1 K= T_T(eau) / 273,16

Vitesse quadratique moyenne v^* des particules d'un gaz :

énergie cinétique moyenne de translation <E_c>=½ m<v²>= ½ mv^*2 = 3/2 kT

d'où v^* = [3kT/m]^½.

Mouvement brownien :

à l'échelle du microscope optique, mouvement aléatoire de particules sous l'action de collisions.

Libre parcours moyen l en fonction du nombre n de particules par unité de volume et de leur section efficace de collision s :

Pendant la durée t entre deux collisions, une particule animée de la vitesse v^*, balaye le volume v^*ts ; de plus le libre parcours moyen est l = v^*t^.

Nombre de particule présent dans ce volume N = n v^*ts =n ls =1 ( entre deux collisions).

Par suite l = 1/(ns)

masse d'une particule : m= M/N_A=29 10^-3 / 6,02 10²³ = 4,82 10^-26 kg.

Vitesse quadratique moyenne v^* = [3kT/m]^½ =[3*1,38 10^-23 *300/4,82 10^-26 ]^½=507 m/s.

Nombre de particules n par unité de volume :

PV = n kT avec V= 1 m³.

n = P/(kT)= 10⁵/(1,38 10^-23 *300) = 2,4 10²⁵ espèces par m³.

Distance moyenne d entre les molécules :

n d³ = 1 soit d = 1/n^1/3 = 1/(2,4 10²⁵)^1/3 =3,5 10^-9 m = 3,5 nm.

section efficace de collision s :

La taille des molécules est de l'ordre de 2 à 3 10^-10 m ; s est de l'ordre de 10^-19 m².

Libre parcours moyen l :

l = 1/(ns) =1/( (2,4 10²⁵ *10^-19)=4,2 10^-7 m= 420 nm.

durée moyenne t entre deux chocs :

t = l /v^* =4,2 10^-7 /507 = 8 10^-10 s = 0,8 ns.

Energie interne :

énergie cinétique et potentielle microscopiques d'un corps.

Capacité thermique C_v à volume constant : C_v = [dU/dT]_V.

La capacité thermique d'un liquide ou d'un solide peut être déterminée par calorimétrie :

Placer dans le calorimètre, une masse m d'un liquide de capacité thermique c connue à la température q ; y ajouter une masse m' de liquide ou de solide, à la température q ', de capacité thermique c' inconnue. A l'équilibre thermique la température est q _éq et : mc(q _éq -q ) + m'c'(q _éq -q ') =0. 

Thermostat : la température d'un thermostat reste constante ; sa capacité thermique est très grande, voir infinie.

Energie cinétique moyenne d'une particule d'un gaz parfait monoatomique : <E_c> =3/2 kT.

Energie interne U d'un gaz parfait monoatomique compenant N particules : U= N<E_c> = 3/2 NkT

Sa capacité thermique C_v molaire à volume constant vaut : C_v = [dU/dT]_V = 3/2kN = 3/2 R.

L'énergie interne d'un gaz réel prend en compte l'énergie potentielle d'interaction entre particules ; l'énergie potentielle dépend de la distance d entre particules ; cette distance d dépend du volume : l'énergie interne d'un gaz réel dépend donc du volume.

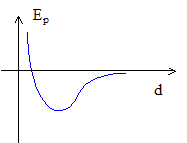
On note m la masse d'un atome. Puisque la molécule est susceptible de vibrer, la distance interatomique d varie dans le temps autour de sa valeur moyenne d₀.

Expression de l'énergie cinétique totale de la molécule en fonction de sa vitesse de translation, de sa vitesse de rotation notée W selon un axe normal à la molécule et de d :

E_c = ½(2m)v² + ½JW²+0,25 m d'² avec J= ½md₀².

Expression de l'énergie potentielle de la molécule en fonction de m et f₀ la fréquence de vibration de la molécule :

On modélise l'interaction inter-atomique par un oscillateur élastique de constante de raideur K

E_p = ½K (d-d₀)² ; l'origine de cette énergie est prise à d=d₀ ;

de plus f₀ = 1/(2p) [K/m]^½ avec m : masse réduite m = ½m.

K= (f₀2p)²m d'où E_p= 0,25m (f₀2p)²(d-d₀)² = m(f₀p)²(d-d₀)².

Nombre de degrés de liberté énergétique de la molécule diatomique : 3 pour la translation, 2 pour la rotation de la molécule linéaire, 2 pour les énergies de vibration.

Chaque degré apporte l'énergie ½kT à l'énergie moyenne de la molécule ; si tous les degrés de liberté de la molécule diatomique étaient excités, l'énergie interne d'un gaz parfait constitué de N molécules serait : U= 7/2NkT ; la capacité thermique molaire C_v serait C_v = 7/2 R.

Relation entre la capacité thermique molaire à pression constante C_p et C_v pour un gaz parfait : C_p = C_v + R.

A température ambiante, la molécule tourne sur elle même mais ne vibre pas : C_v = 5/2 R ; C_p = C_v + R= 7/2 R ;

L'air étant contitué de molécules linéaires ( O₂, N₂, CO₂ ), pour ce dernier g= C_p/C_v =7/5 = 1,4.