Aurélie 20/12/06
 

Agrégation 2006 : Etude macroscopique de l'élasticité d'un fil.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Soit un fil caractrisé par sa température T, sa tension f et sa longueur L. On note CL sa capacité thermique à L constant et k = T[dS/dL]T.

Expression du travail élémentaire reçu lors d'une variation de longueur dL : dWrév = f dL

Expression de la différentielle de son entropie S(T, L) : dS= CL/T dT + k /T dL

Expression de la différentielle de son énergie interne U(T, L) : dU=TdS+f dL = CLdT +(k +f )dL.

Relations de Clapeyron permettant le calcul de k et des variations de CL à température constante à partir de l'équation d'état liant f, T et L.

U est une fonction d'état : [dCL/dL]T= [d(k +f )/dT]L.

S est une fonction d'état : 1/T[dCL/dL]T=[d(k /T)/dT]L= 1/T[dk/dT]L-k/T2.

[dCL/dL]T=[dk/dT]L-k/T.

par suite : [dk/dT]L-k/T= [d(k +f )/dT]L = [dk /dT]L + [df /dT]L ; -k/T=[df /dT]L ; k= - T[df /dT]L.

Or [dCL/dL]T=[dk/dT]L-k/T et [dk/dT]L = - [df /dT]L -T [d2f /d2T]L d'où [dCL/dL]T= -T [d2f /d2T]L.

L'expérience met en évidence une loi de Hooke dans le domaine élastique f = K(T)(L-L0) où K ne dépend que de T. On considère également que CL est une constante.

k= -T[df /dT]L=-T K'(L-L0) ;

[dCL/dL]T= -T [d2f /d2T]L= -T K"(L-L0) = 0 car CL est une constante ; par suite K"=0 ce qui implique K'= constante et K = AT+B, A et B constants.

K est donc une fonction affine de la température.

Expression de l'entropie du fil :

dS= CL/T dT + k /T dL avec CL constant et k =-T K'(L-L0) = -TA(L-L0)

dS=CLd(lnT)-A(L-L0)dL

S-S0=ln(T/T0)-½A(L-L0)2.

Expression de l'énergie interne du fil :

dU= CLdT +(k +f )dL avec CL constant et k = -TA(L-L0) et f = (AT+B)(L-L0) ; k +f = B(L-L0)

U-U0 = CL(T-T0) + ½B(L-L0)2.

Variation isotherme de l'énergie libre F du fil : F=U-TS

DF= U-U0 -T(S-S0)=CL(T-T0) + ½B(L-L0)2-T(ln(T/T0)-½A(L-L0)2)

à température constante DF=½B(L-L0)2+½AT(L-L0)2) = ½K(L-L0)2) c'est à dire l'énergie potentielle élastique.

On réalise l'expérience suivante :

Un fil, dont une extrémité est fixe, est tendu par une masse M. La masse repose sur une balance électronique, tout en conservant le fil tendu. Le fil est alors chauffé avec un briquet et on observe l'évolution de la valeur de la masse m indiquée par la balance.
Relation entre f, M et m :

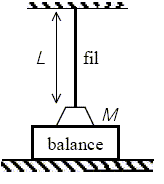
La masse M est soumise à son poids, vertical, vers le bas, valeur Mg ; à l'action de la balance , verticale, vers le haut , valeur mg; à la tension du fil f, verticale, vers le haut.

A l'équilibre ces trois forces se neutralisent, d'où : f =(M-m)g.

Pour un fil métallique m croît avec la température, alors que pour un fil de caoutchouc m décroît.

Signes de k et A pour chaque fil :

f =(M-m)g donne [df /dT]L = -g[dm /dT]L

de plus k= -T[df /dT]Ld'où k= gT[dm /dT]L. k a le signe de [dm /dT]L, positif pour le métal, négatif pour le caoutchouc.

Enfin f = K(T)(L-L0) = (AT+B)(L-L0) donne : [df /dT]L =A =-g[dm /dT]L.A a le signe de -[dm /dT]L, négatif pour le métal, positif pour le caoutchouc.

Coefficient a de dilatation à tension constante : a = 1/L[dL/dT]f.

f = K(T)(L-L0) donc à tension constante, (L-L0) et K(T) varient en sens contraire.

Pour le métal A<0, donc [dL/dT]f>0 d'où a >0 ; Pour le caoutchouc A>0, donc [dL/dT]f<0 d'où a<0.

retour -menu