|
enseignement, concours, caplp interne 2006 : lois de Descartes ; lame mince et fibre optique En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
| .
. |
|||
|
|||
|
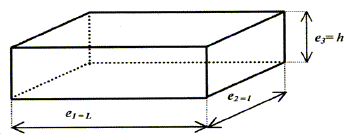
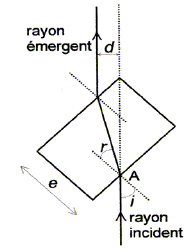
Dans l'étude qui suit on utilise un parallélépipède rectangle : celui-ci représente un système de 3 lames à faces parallèles d'apaisseur e1 = L; e2 = l et e3 = h.
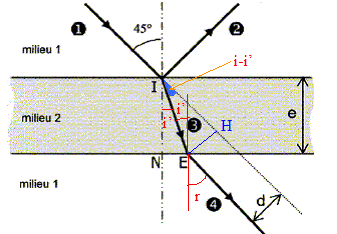
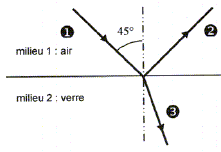
Un rayon lumineux (1) vient frapper la surface plane d'une lame de verre. Au contact de la surface entre l'air et le verre, ce rayon donne naissance à deux autres rayons lumineux : un rayon (2) qui se propage dans l'air et un rayon (3) qui se propage dans le verre.
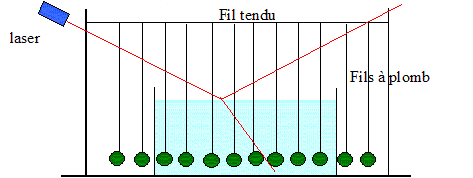
On note i' la mesure de l'angle de réflexion et r la mesure de l'angle de réfraction. Nom de chaque rayon lumineux : (1) : rayon incident ; (2) rayon réfléchi ; (3) rayon réfracté ou transmis. Le milieu le plus réfringent est le verre, milieu d'indice le plus élevé. Dans l'expéreince suivante, tous les fils à plomb sont frappés par le faisceau laser : les rayons incident, réfléchi, et réfracté sont donc dans le même plan.
Loi de la réflexion : la valeur de l'angle d'incidence i est égal à la valeur de l'angle de réflexion i'. Loi de la réfraction : n1 sin i = n2 sin r sin r = 1 sin 45 / 1,5 =0,471 ;
r =
28°.
Montrons que les faisceaux incident et transmis ( émergent) sont parallèles : en I : n1 sin 45 =n2 sin i' ; en E : n2 sin i' =n1 sin r ; d'où n1 sin 45 =n1 sin r soit r = 45°. Expression de d en fonction de i, i' et IE : d = EH= IE sin ( i-i') Expression de e en fonction de i' et IE : e = IN = IE cos i' Expression de d en fonction de e, i et r : d = e sin ( i-i') / cos i' A.N : i=45° ; i'=28 ; e= 5,0 mm. d= 5,0 sin (45-28) / cos28 =5*0,292
/0,882 =1,7
mm.
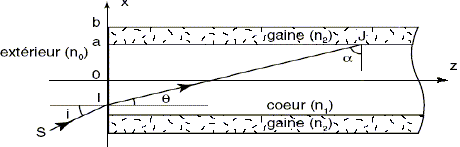
Fibre optique multimodale à saut d'indice : Une fibre optique est constituée d'un coeur cylindrique transparent en silicium de rayon a et d'indice n1. Ce coeur est entouré par une gaine transparente en silicium dopé d'indice n2 < n1. Un revétement plastique protège l'ensemble.
Relations entre les angles i et q d'une part et q et a d'autre part : en I : n0 sin i = n1 sin q (1) ; q + a = 90° d'où sin q = cos a (2) L'intérêt est de conserver dans le coeur de la fibre la totalité de l'énergie transportée par le rayon lumineux : pour cela, on met à profit le phénomène de réflexion totale à l'interface coeur-gaine. On recherche alors l'expression liant a lim , n1 et n2. Au point J, il y a réflexion totale si : n1 sin a lim = n2 sin 90 = n2 soit sin a lim = n2 / n1(3) Condition pour que le rayon lumineux reste dans la fibre : (1) et (2) donnent : n0 sin i = n1 cos a ou sin2 i = (n1/n0)2 cos 2 a Or cos 2 a = 1 -sin 2 a d'où : sin2 i = (n1/n0)2(1 -sin 2 a ) il y a réflexion totale si sin a >= n2 / n1 soit sin 2 a >=( n2 / n1)2 ou en core : 1 -sin 2 a <= 1-( n2 / n1)2 sin2 i <= (n1/n0)2[1-( n2 / n1)2] ; sin i <=[(n12-n22) / n02]½. A.N : n0 = 1,000 ; n1 = 1,460 ; n2 = 1,454 sin i <=[1,462-1,4542)/12]½ ; sin i <=0,132 ; i<= 7,60 °. Avantages de la fibre optique par rapport au câble électrique : Les champs magnétiques ne perturbent pas la transmission ; absence de dégagement de chaleur par effet joule ; vitesse de transmission très élevée ; faible risque de perte du signal lors d'une transmission à grande distance. |
|||
|
|
|||
|
|
 n1
= 1,0 ; n2 = 1,5 ; i = 45°
n1
= 1,0 ; n2 = 1,5 ; i = 45°