Pile et appareils nomades : piles à hydrogène, radioactivité, condensateur bac S France septembre 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

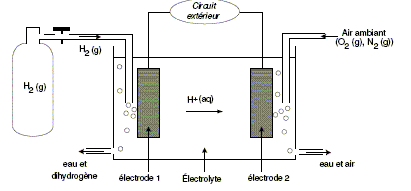
Principe d'une pile à hydrogène: La pile à hydrogène présente des avantages importants en termes d’environnement (rejets non polluants au cours de son utilisation et absence de nuisance sonore). Elle est constituée de deux électrodes à la surface desquelles ont lieu les réactions chimiques d’oxydoréduction et d’un électrolytedans lequel se déplacent les ions.    Au niveau de l’électrode 1, les molécules de dihydrogène H2 , provenant d’un réservoir, sont oxydées en ions H+ , qui se déplacent dans la solution électrolytique. Au niveau de l’électrode 2, des électrons, des ions hydrogène H+ de l’électrolyte et des molécules de dioxygène O2 , provenant de l’air ambiant, se combinent pour donner de l’eau. Données :couples oxydant/réducteur : H+ (aq)/H2 (g) et O2 (g)/H2O ( l ) Volume molaire d’un gaz Vm dans les conditions d’utilisation de cette pile : Vm = 24 L/mol. Écrire la demi-équation électronique qui correspond à l’oxydation du dihydrogène. H2 (g) = 2 H+ (aq) + 2e-. Préciser le sens de circulation du courant électrique dans le circuit extérieur. Au niveau de l'électrode 1, l'oxydation de H2 libère des électrons : dans le circuit extérieur, les électrons vont de l'électrode 1 vers l'électrode 2. Le sens conventionnel du courant électrique est en sens contraire du sens de déplacement des électrons : de l'électrode 2 vers l'électrode 1. Dans la suite de la partie 1, on écrira l’équation de la réaction modélisant la transformation chimique qui a lieu au sein de la pile lors de son fonctionnement : O2 (g) + 2 H2 (g) = 2 H2O(l) . Expliquer pourquoi le dihydrogène est le réactif limitant. Le dioxygène provient de l'air, donc de l'atmosphère. La quantité de matière de dioxygène de l'air est bien supérieure à la quantité de matière de dihydrogène contenu dans le réservoir. On note ni (H2 ) la quantité initiale de dihydrogène. En exploitant la demi-équation, donner l’expression de la quantité d’électrons échangés n(e -) en fonction de ni (H2 ). H2 (g) = 2 H+ (aq) + 2e-. D'après les nombres stoechiométriques : n(e -) = 2 ni (H2 ). On note I l’intensité moyenne du courant électrique au cours du fonctionnement de la pile. On suppose que la pile s’arrête de fonctionner lorsque le réactif limitant est épuisé au bout d’une durée notée Dt. Déterminer l’expression littérale de la quantité de matière ni (H2 ) du réactif limitant en fonction de l’intensité I, de la durée Dt, de la constante d’Avogadro NA et de la charge élémentaire e. D'une part Q = I Dt ; d'autre part Q = n(e-) e NA et de plus n(e-) = 2 ni (H2 ) D'où I Dt = 2ni (H2 )e NA ; ni (H2 ) = I Dt / (2e NA). Réservoir de stockage Pour une durée de fonctionnement de 200 h et pour une intensité moyenne du courant électrique débité par la pile égale à 200 A, la quantité de matière du réactif limitant est ni (H2 ) = 7,5 × 102 mol. Calculer le volume V(H2 ) du réservoir de stockage nécessaire dans les conditions usuelles de température et de pression. Aide aux calculs :7,5/24 = 3,1 ; 2,4/7,5 = 0,32 ; 2,4*7,5 =18. V = n Vm = 7,5 *100 *24 = 7,5*2,4*1000 = 18*1000 = 18 103 L = 18 m3. Au regard de ce résultat, quel inconvénient peut présenter l'utilisation de la pile à hydrogène dans les conditions usuelles de température et de pression ? Le volume de stockage du carburant est énorme.   Prototype de pile miniature. 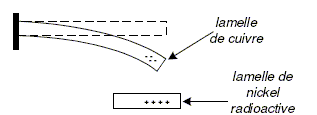Des scientifiques de l’université Cornell (USA) ont conçu un prototype de pile miniature constituée de deux lamelles superposées, légèrement espacées : celle du dessous est initialement composée de nickel 63 ( 63Ni), un matériau radioactif qui émet des électrons ; celle du dessus est en cuivre. Lorsque des électrons qui s’échappent du nickel atteignent la lamelle de cuivre, elle se charge négativement. Attirée par la lamelle de dessous, dont la charge devient positive, elle se plie, se décharge par contact et revient à l’état initial. L’énergie mécanique de ce mouvement est transformée en énergie électrique à l’aide d’un système piézo-électrique qui génère de l’électricité quand il est déformé. Si le rendement électrique d’un tel dispositif est faible, son encombrement est particulièrement réduit (les scientifiques espèrent parvenir à construire une pile de 1 cm3) et sa durée de fonctionnement devrait dépasser plusieurs dizaines d’années. D’après un extrait de «Ordinateur individuel On donne : 27Co ; 28Ni ; 29Cu. Quel est le type de transformation radioactive du nickel 63 ? Emission d'électron, donc radioactivité de type b-. Compléter l'équation de désintégration radioactive du nickel 63 en identifiant le noyau formé. 6328Ni ---> AZX +0-1e . Conservation de la charge : 28 = Z-1 d'où Z = 29 : on identifie X à Cu. Conservation du nombre de nucléons : 63=A+0. 6328Ni ---> 6329Cu +0-1e . On note N(t) le nombre de noyaux radioactifs de nickel présents dans la pile à l’instant t et N0 le nombre de ces noyaux présents à un instant t0 = 0 pris comme origine des dates. La constante radioactive du nickel 63 vaut l = 6,9 × 10 - 3 an- 1. Rappeler la loi de décroissance radioactive N(t) en fonction N0 et l. N(t) = N0 e(-lt). Donner la définition du temps de demi-vie t1/2 d’une source radioactive. Durée au bout de laquelle l'activité initiale a été divisée par deux. Durée au bout de laquelle le nombre de noyaux initiaux est divisé par deux. Montrer que t½ = ln2 / l. d'une part : N(t) = N0.e-l.t ; d'autre part à t=t½ , N(t½) = ½ N0 = N0.e-l.t½ ; d'où ½ = e-l.t½ ; ln ½ = -l.t½ ; ln2 =l.t½ ; t½ = ln2 /l Calculer t½. Aide au calcul : ln2 = 0,69. t½ = 6,9 10-1 / 6,9 × 10 - 3 =1/10-2 = 1,0 102 ans. Ce résultat est-il en accord avec celui indiqué dans le document ? La source radioactive devient pratiquement inactive au bout d'environ 8 demi-vie soit environ 800 ans.  "sa durée de fonctionnement devrait dépasser plusieurs dizaines d’années" : donc accord avec le texte. Principe de l’horloge d’un appareil nomade. Tous les appareils nomades ont besoin d’une horloge (alimentée par une pile). Dans ce paragraphe on va étudier l’évolution temporelle d’un circuit (R,C) qui fait partie de l’horloge. 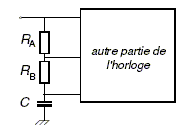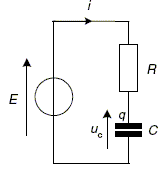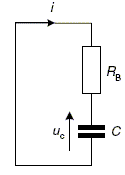Dans un premier temps le condensateur, initialement décharge, de capacité C est chargé à travers les conducteurs ohmiques de résistances RA et RB. On note E la tension aux bornes du générateur. Lors de cette étape, on considère que les conducteurs ohmiques et le condensateur de capacité C = 22 mF sont branches en série. Le circuit équivaut alors à : ( avec R = RA + RB = 66 kW ). Donner la relation qui lie l’intensité instantanée i(t) du courant électrique qui circule dans le dipôle (R,C) à la charge instantanée q(t) de l’armature du condensateur notée sur la figure, puis à la tension uC(t). i(t) = dq(t) /dt ; q(t) = C uC(t) d'où : i(t) = C duC(t) /dt. Déterminer, en justifiant la réponse, l’équation différentielle qui régit l’évolution de la tension uC(t) aux bornes du condensateur au cours de sa charge. Additivité des tensions : E = Ri + uC ; or i = CduC /dt. par suite E= RCduC/dt + uC. Dès que la tension uC(t) aux bornes du condensateur atteint une valeur de référence Umax=2E/3, le reste de l’horloge change d’état électrique et fait décharger le condensateur à travers le seul conducteur ohmique de résistance RB = 33 kW . Le circuit équivaut alors à celui qui est représenté : Déterminer, en justifiant la réponse, l’équation différentielle qui régit l’évolution de la tension uC(t) aux bornes du condensateur au cours de sa décharge dans le conducteur ohmique de résistance RB. Additivité des tensions : 0 = RBi + uC ; or i = CduC /dt. par suite 0= RBCduC/dt + uC. 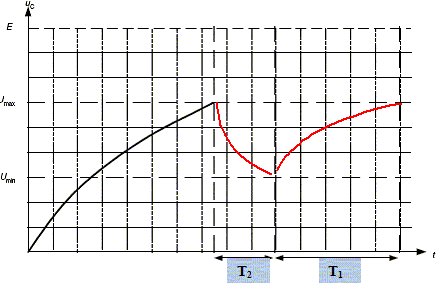Dès que la tension uC(t) aux bornes du condensateur atteint une autre valeur de référenceUmin=E/3, le reste de l’horloge change d’état et impose un nouveau cycle de charge du condensateur puis de décharge, etc. La durée de charge du condensateur, entre Umin et Umax, est notée T1 et celle de la décharge, jusqu’à Umin, notée T2. Sachant que les durées de charge et de décharge sont proportionnelles aux constantes de temps du circuit, expliquer, sans calcul, pourquoi la valeur de T1 est supérieure à celle de T2. T1 est proportionnelle à t1=(RA+RB)C ; T2 est proportionnelle à t2=RBC ; RA+RB est supérieur à RB, donc T1 est supérieur à T2. Compléter, l’allure générale de l’évolution au cours du temps de la tension uC(t) lors des différentes phases de charge et de décharge.

retour -menu