Chute verticale d'un ballon ( Euler) bac S Polynésie 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

On étudie la chute d'un ballon de baudruche gonflé, de volume V. Le ballon est lesté d'une bille de volume négligeable devant V. Yvan lâche le ballon sans vitesse initiale tandis qu'Amélie en face, réalise une vidéo de la chute. Ils constatent que le ballon est en mouvement de translation vertical. Une règle de 1,00 m est placée en position verticale dans le champ de la caméra. L'origine O de l'axe correspond au centre du ballon sur la première image juste après le lâcher du système. L'origine des dates correspond également à cette image. Après traitement des données on obtient : vlim = 2,75 m s-1 ; temps caractéristique t = 0,43 s. La valeur de la force de frottement fluide exercée sur le système est proportionnelle au carré de la vitesse. Masse du système : M=10,7 g ; V= 3,05 L Masse volumique de l'air : r = 1,20 g/L ; g = 9,81 m s-2. Donner l'expression littérale des valeurs des forces s'exerçant sur le système au cours de la chute. 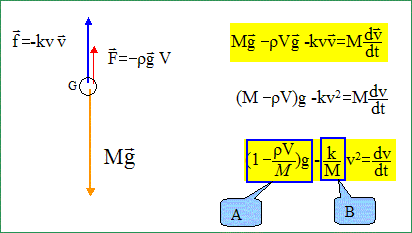Poids, verticale, vers le bas P=Mg. Poussée d'Archimède, verticale, vers le haut, valeur : poids du volume d'air déplacé : F = rVg. Force de frottement fluide, verticale, vers le haut, valeur f= kv2 ( k est une constante). Etablir l'équation différentielle vérifiée par la vitesse du centre d'inertie du système.  Montrer qu'elle peut se mettre sous la forme dv/dt = A-Bv2. Montrer que A= 6,45 S.I. Préciser son unité. A= (1-1,2*3,05 /10,7)*9,81 = 6,45 m s-2. Montrer que B= A/ v2lim. Calculer B. Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme : dvlim/dt=0 L'équation différentielle s'crit : A-B v2lim=0 ; B= A/ v2lim. B = 6,45 / 2,752 = 0,853 m-1. Bv2 a la dimension d'une accélération ( L T-2) ; [v2] =L2 T-2 B a la dimension d'une accélération divisée par le carré d'une vitesse : B a la dimension de l'inverse d'une longueur. Feuille de calculs du tableur. t(s) y(m) vexp(m/s) v(m/s) 1 0 0 0 0 2 0,040 0,010 0,39 0,26 3 0,080 0,031 0,64 0,51 4 0,120 0,061 0,76 0,76 5 0,160 0,092 0,90 1,00 6 0,200 0,133 1,15 1,22 7 0,240 0,184 Les valeurs de la colonne t(s) représentent les dates de chaque image. 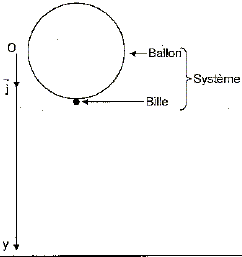Les valeurs de la colonne y(m) représentent les ordonnées correspondantes du centre du ballon, donc la distance parcourue. vexp : valeurs expérimentales de la vitesse ; v : vitesses données par la méthode d'Euler. Quelle est le rôle de la règle de 1,00 m placée à côté du ballon ? La règle permet de définir l'échelle sur l'axe vertical ; elle permet également de repèrer le centre O du ballon. En utilisant les valeurs des cellules pertinentes des colonnes t(s) et y(m) du tableau, déterminer vexp à la date t = 0,200 s. vexp(t) = [y(t+1) - y(t-1)] / (2Dt ) avec Dt = 0,040 s. vexp(t= 0,2 s) = y(0,24)-y(0,16) / 0,08 = (0,184-0,092)/0,08 =1,15 m/s. A partir de l'équation différentielle, en utilisant la méthode d'Euler, déterminer la valeur de v à la date t=0,200 s. Equation différentielle : a(t) = 6,45 -0,853 v2(t) a(0,16) = 6,45 -0,853 *12 =5,597 m s-2. v(t+Dt) = v(t) +a(t) .Dt. v(0,2) = 1+5,597*0,04 =1,22 m/s.   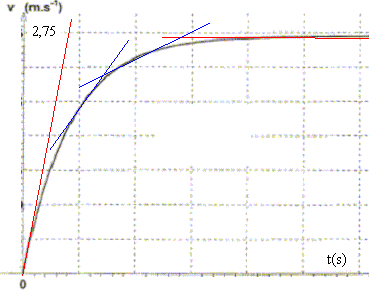Courbe v(t) obtenue par la méthode d'Euler. L'objectif de cette dernière partie n'est pas de tracer précisément la courbe point par point v(t) obtenue par la méthode d'Euler mais de donner son allure et de l'exploiter. Tracer l'allure de la courbe v=f(t) en y indiquant la vitesse limite et le temps caractéristique t. Indiquer deux régimes sur le graphe et les nommer. Justifier que le tracé de la tangente à la courbe v=f(t) permet d'évaluer la valeur de l'accélération à chaque instant. En déduire , en le justifiant, l'évolution de cette accélération au cours du temps des deux régimes. L'accélération est la dérivée de la vitesse par rapport au temps. A une date donnée, tracer la tangente à la courbe v(t) : son coeficient directeur donne l'accélération. Au cours du temps les tangentes se rapprochent de l'horizontale : les coefficients directeurs diminuent jusqu'à s'annuler lorsque le régime permanent est atteint.

retour -menu