Concours manipulateur électroradiologie médicale Clermond Ferrand 2008 radioactivité, travail, énergie cinétique et potentielle, acide base En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

L'année lumière correspond-elle à l'intervalle de temps que met la lumière pour parcourir la distance de 9,46 1012 km ? Vrai. Distance parcourue par la lumière dans le vide à la vitesse c=3 108 m/s pendant une année. 1 an = 365,25*24*3600 ; T = 3,16 107 s. D= c T = 3 108 *3,16 107 = 9,46 1015 m = 9,46 1012 km. Quel est le travail du couple qu'il faut exercer pour tordre, d'un angle q, un fil dant la constante de torsion est C ? Expression d'un couple de torsion G = C q avec q en radian. Expression du travail élémentaire au cours de la torsion d'un angle très petit noté dq : dW = C q dq Intégrer entre 0 et q pour le travail au cours de la torsion d'un angle q : W = ½Cq2.   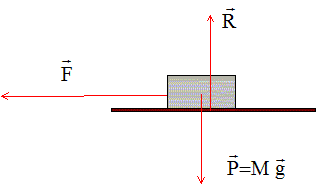Quelles sont dans le système internationnal les unités de force, de travail, de puissance et de vitesse angulaire ? Force : newton ( N) ; travail : joule (J) puissance : watt (W) ; vitesse angulaire : radian/seconde ( rad s-1)   Un noyau instable de polonium 21084Po donne un noyau de plomb en émettant une particule alpha. Ecrire en la justifiant, l'équation nucléaire traduisant cette réaction. 21084Po --> AZX +42He Conservation de la charge : 84=Z+2 ; Z=82 Conservation du nombre de nucléons : 210=A+4 ; A = 206. 21084Po --> 20682Pb +42He. Dans une fête foraine, un jeu consiste à pousser le plus fort possible, un chariot sur des rails, afin qu'il atteigne une cible. Les rails possèdent une partie horizontale AB longue de 1,2 m, puis une partie ascendante, la cible étant placée à une hauteur de 2,4 m par rapport au niveau AB. Sur la piste AB un joueur exerce sur le chariot de masse m=5,0 kg, une force constante d'intensité F= 120 N parallèle et de même sens que le vecteur vitesse du chariot. En négligeant les frottements et en prenant g = 10 N/kg : Calculer l'énergie cinétique acquise par le chariot en B. Le poids et l'action du plan, perpendiculaire à la vitesse, ne travaillent pas. Travail de la force motrice F au cours du déplacement AB : W = F AB. Variation de l'énergie cinétique entre A et B : ½mv2B -0 ( vitesse initiale nulle) Ecrire le théorème de l'énergie cinétique entre A et B : Ec= ½mv2B = F AB ; Ec = F AB = 120*1,2 =144 J. Préciser si le chariot ainsi propulsé par le joueur peut atteindre la cible. Pour atteindre la cible l'énergie cinétique en B va être convertie en énergie potentielle de pesanteur. Energie potentielle de pesanteur du chariot atteignant la cible : La référence de l'énergie potentielle de pesanteur est prise en B : Ep cible = mgh Ep cible = 5*10*2,4 =120 J. L'énergie cinétique du chariot en B est suffisante pour lui permettre d'atteindre la cible. En réalité le chariot monte seulement à une hauteur de 1,9 m. Pourquoi n'a t-il pas atteint la cible ? Le chariot est soumis à des frottements sur les rails : une partie de l'énergie cinétique en B est ainsi convertie en énergie thermique.   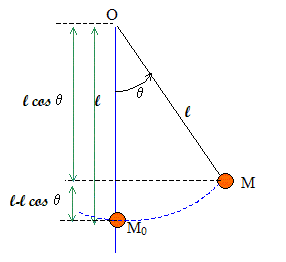Un pendule simple est écarté de sa position d'équilibre d'un angle q =60°. L'objet suspendu, de masse m=200 g, est assimilable à un objet ponctuel ; la longueur du fil est L=1,6 m Calculer l'énergie potentielle du système terre pendule. Le plan horizontal contenant l'objet à la position d'équilibre sera choisi comme plan de référence de l'énergie potentielle de pesanteur. Energie potentielle de pesanteur : Ep (M) = m g L( 1 - cosq). Ep (M) = 0,2 *10*1,6(1-cos60) = 1,6 J. Calculer la vitesse avec laquelle le pendule passe par la position d'équilibre. Energie mécanique du système au point le plus haut : 1,6 J Energie mécanique du système en M0 : ½mv2. Conservation de l'énergie mécanique : ½mv2 = 1,6 v =(3,2/m)½ =(3,2/0,2)½ = 4 m/s. Rappeler les définitions : d'un acide : espèce, ion ou molécule susceptible de céder un proton H+. du pH d'une solution aqueuse : le pH d'une solution aqueuse est défini à partir de la concentration en ion oxonium H3O+, exprimée en mol/L, par la relation : pH = - log [H3O+]. d'un acide fort en solution aqueuse : La réaction entre un acide fort et l'eau est totale : l'acide fort est entierement ionisé en solution aqueuse. de la constante d'acidité d'un couple acide base. Soit le couple acide / base AH/A- et le couple H3O+/H2O. Réaction acide base : AH + H2O = H3O++ A- . La consatant d'acidité est la constante d'équilibre de cette réaction : Ka = [H3O+][A-] /[AH]   Justifier ou réfuter les affirmations ci-dessous. La justification sera faite en 3 ou 4 lignes au maximum, puis illustrée par un exemple numérique si vous pensez que c'est vrai. La réfutation sera aussi justifiée en quelques lignes et sera appuyée par un contre exemple numérique, si vous pensez que c'est faux. A propos de solutions aqueuses de monoacides dont les concentrations sont comprises entre 10-1 et 10-5 mol/L, on énonce les affirmations suivantes : Dans le cas d'un acide fort la connaissance de la concentration est suffisante pour en déduire le pH. Vrai. L'acide fort est entièrement dissocié en solution. L'avancement final est égal à l'avancement maximal. [H3O+] = xmax/V = c, concentration en soluté apporté. Par suite pH = - log c. Exemple : acide chlorhydrique tel que c = 10-2 mol/L ; pH = - log c = - log 0,01 = 2. Entre deux acides celui dont la solution a le pH le plus faible, est le plus fort. Faux. Il faudrait préciser " à concentration égale ...." L'acide le plus fort correspond à l'acide le plus ionisé ( taux d'avancement final le plus proche de 1), c'est à dire libérant un plus grand nombre d'ion oxonium H3O+ en solution. Contre exemple : acide chlorhydrique, acide fort, à c = 10-3 mol/L : pH = 3. acide méthanoïque, acide faible : concentration 0,1 mol/L : pH= 2,4 concentration 10-3 mol/L : pH= 3,4. Données : acide méthanoïque / ion méthanoate Ka = 1,8 10-4. concentration 0,1 mol/L : pH= 2,4 concentration 10-3 mol/L : pH= 3,4.

retour -menu