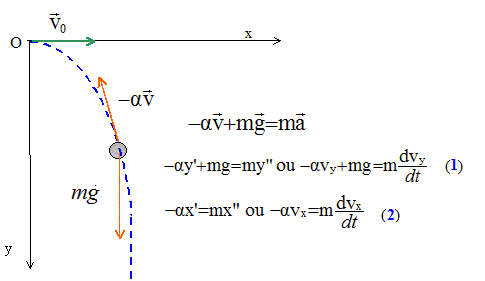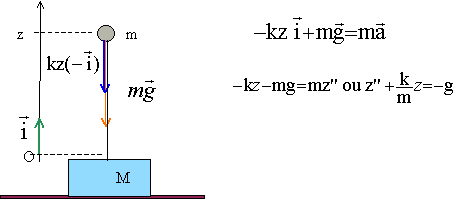|
Concours d'ingénieurs ECE 2007
; QCM de mécanique En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts |
|||||||||
| .
. |
|||||||||
|
|||||||||
|
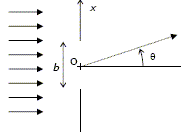
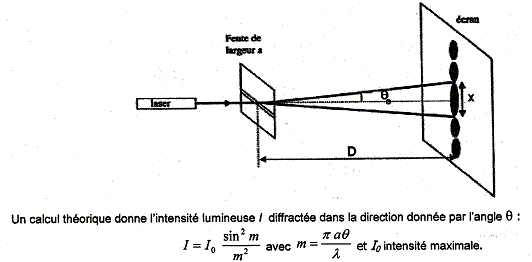
Le rayonnement est situé dans le domaine infrarouge. Vrai. Le domaine visible s'étend de 400 à 800 nm ; au delà de 800 nm commence le domaine IR. La diffraction est le phénomène d'élargissement des faisceaux lumineux et plus généralement des ondes progressives derrière des obstacles limitant leurs dimensions transversales. Vrai. La diffraction est l'éparpillement de la lumière dû à la limitation matérielle des ondes. Ce phénomène se manifeste dès qu'un rayon lumineux rencontre un obstacle de même ordre de grandeur que sa longueur d'onde. L’onde diffractée a une fréquence double par rapport à l’onde incidente. Faux. La fréquence de l'onde est inchangée. Ce faisceau lumineux parallèle monochromatique de longueur d'onde l0 éclaire en incidence normale un diaphragme formé dans un écran opaque plan par une fente infiniment longue de largeur b. Soit O un point origine au milieu de la fente et Ox l'axe perpendiculaire à la fente dans le plan de l'écran.
L’intensité lumineuse I décroît à partir de q= 0 et s'annule pour la première fois lorsque sin q=l0 /b. Vrai. Sur la figure ci-dessous à la place de b on a noté a.
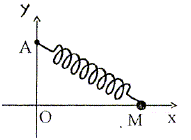
On considère sur la figure ci-dessous le ressort de raideur k et de longueur à vide l0 dont une extrémité est fixée au point A(x = 0 ; y = l0) et dont l'autre extrémité est fixée à un point matériel M de masse m, qui est libre de se déplacer sans frottement le long de l'axe horizontal Ox. On pose x la valeur algébrique du vecteur OM sur l'axe Ox.
L'énergie potentielle du point matériel M en fonction de x et des données est : Ep= ½k(l-l0)2. Vrai. Il faut préciser que l'origine de l'énergie potentielle élastique est le point O, la position d'équilibre. x=0 est la seule position d'équilibre.Vrai. L'énergie potentielle élastique est minimale au point O. A l'instant t = 0, on abandonne M en x = l0 avec une vitesse initiale nulle. L'énergie cinétique du point matériel M au moment où il passe au point O en fonction des données est : Ec(x=0)= ½kl0(2½-1)2. Faux. En absence de force dissipative ( frottement) , l'énergie mécanique se conserve: L'énergie mécanique initiale est sous forme potentielle : ½k(l-l0)2 avec l = 2½l0 ; EM= Ep(0) = ½kl02( 2½-1)2 . En x=0, l'énergie mécanique est sous forme cinétique ; la conservation de l'énergie mécanique conduit à : Ec(x=0)= ½kl02( 2½-1)2 . La vitesse du point M à ce moment là est : (k/m)½l0(2½-1). Vrai. ½mv2(x=0) =½kl02( 2½-1)2 ; v(x=0) = (k/m)½ l0 (2½-1).
Un promeneur de masse M = 70 kg effectue une marche de 10 kilomètres à vitesse constante sur une route horizontale (g = 10 m.s-2) avec une longueur de pas p de 50 cm. On suppose dans un premier temps que le centre de masse du promeneur conserve une altitude constante pendant la marche et que le contact sol-promeneur se fait sans glissements. En modélisant le promeneur par un solide, le travail des forces intérieures effectué au cours de la marche est nul. Vrai. Le mouvement étant rectiligne uniforme ( valeur constante de la vitesse) , la somme vectorielle des forces est nulle : la somme des travaux de ces forces est nulle. Le corps humain n’est pas un corps solide. Au cours de la marche, le centre de marche effectue des oscillations. L’ordre de grandeur de l’amplitude de ces oscillations est a = 1 cm pour chaque pas effectué. Quand le centre de masse s’élève, l’énergie élastique musculaire est transformée en énergie potentielle. Quand le centre de masse s’abaisse, l’énergie potentielle est convertie en énergie thermique (« chaleur »). Cette marche est équivalente pour le travail fourni à l’escalade d’une montagne d’une hauteur H de 500 m. Faux. Nombre de pas : 10 000 / 0,5 = 20 000 pas ; à chaque pas le centre d'inertie s'élève de 1 cm puis s'abaisse de 1 cm ; hauteur "équivalente" :2* 20 000*0,01 = 400 m. L’énergie mécanique fournie par le marcheur est de 280 kJ. Vrai. A chaque pas le centre d'inertie s'élève de 1 cm puis s'abaisse de 1 cm ; l'énergie mécanique mise en jeu est : mgh = 70*10*400 = 280 k J. L’énergie mécanique fournie par le marcheur est beaucoup plus importante que l’énergie de la ration alimentaire quotidienne, environ de grandeur de 106 J, d’un homme sédentaire. Faux. 10 6 J = 1000 kJ ;
280 k J < 1000 kJ.
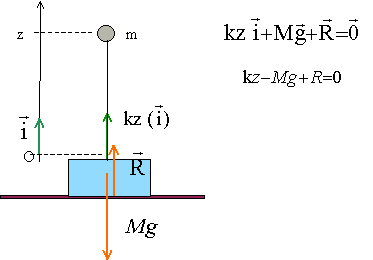
L’équilibre des forces s’exerçant sur le bloc s’écrit : -Mg + R + kz = 0 avec R réaction entre le socle et le bloc. Vrai.
La hauteur maximale atteinte sans que le boc décolle est zmax = Mg/k. Vrai. A la limite du décollage du bloc M, l'action du socle s'annule R=0 d'où zmax = Mg/k. La vitesse maximale v0 est telle que : v02 = g2(M2+2mM)/(mk). Vrai. Energie mécanique initiale du système {balle + fil élastique} : ½ mv02. Energie mécanique du système à l'altitude zmax : ½kz2max + mgzmax. Soit en remplaçant zmax par Mg/k : ½M2g2/k + mg2 M/k = ½g2 /k [ M2 +2mM] L'énergie mécanique se conserve : ½ mv02 = ½g2 /k [ M2 +2mM] v02 =g2 /(km) [ M2 +2mM]
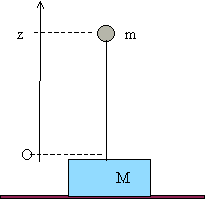
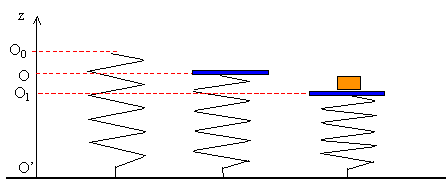
On considère un ressort de raideur k et de masse négligeable, coulissant le long d’une tige rigide d’axe O’z. Son extrémité inférieure noté O’ est fixe. En l’absence de charge, l’extrémité supérieure située en O0. On fixe à cette extrémité un disque horizontal de rayon r, de masse M et négligeable, percé en son centre et coulissant le long de O’z. Lorsque le disque est au repos trouve en O. On enfile sur la tige O’z un anneau de masse m que l’on pose sur le disque.
La nouvelle position d’équilibre O1 du disque est distante de O de |OO1 | = mg/k. Vrai. Equilibre de l'anneau soumis à son poids ( valeur mg) et à la tension du ressort ( valeur k|OO1| si on choisit O comme origine) mg = k|OO1| soit |OO1 | = mg/k. On abaisse le disque porteur de l’anneau d’une hauteur a à partir de la position d’équilibre O1 et on le lâche sans vitesse initiale. On repère les déplacements z du disque à partir de la position d’équilibre O1 et on considère que l’anneau et le disque sont solidaire et que le mouvement s’effectue sans frottements. L’origine du temps est prise à l’instant t=0. L’équation différentielle qui régit le mouvement du disque porteur et de l’anneau peut s’écrire : z" -k/(M+m) =0. Faux. mais plutôt : z" + k(M+m) z = 0. La solution de l’équation différentielle qui régit le mouvement du disque porteur et de l’anneau est : z(t) = -a cos (wt) avec w 2 = k/(M+m). Vrai. Les forces qui s’exercent sur l’anneau sont son poids et la réaction de disque sur l’anneau. Vrai. L'anneau est un élément du système {anneau + disque} ; l'anneau est toujours en contact avec le disque ; l'anneau est en équilibre sous l'action de son poids et de l'action du disque. |
|||||||||
|
|
|||||||||
|
|