Etude d'un haut parleur : oscillations libres, oscillations forcées concours technicien laboratoire 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

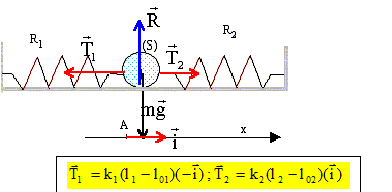
On s'interesse au système de suspension d'un haut pareleur électrodynamique ( oté par la suite HP). Il est constitué par le dôme de la bobine reliée à la carcasse par le spider, ressort placé autour. Ce système est en outre relié à la membrane du HP qui met en vibration l'air ambiant en produisant un son.  Etude expérimentale d'un modèle simplifié : oscillations libres Dans un premier temps on se limite au système oscillant constitué par le dôme et le spider. Ce système est assimilable à un solide de masse m = 50,0 g contraint à un déplacement rectiligne horizontal, et relié à deux ressorts toujours allongés et tendus grâce à deux points fixes. 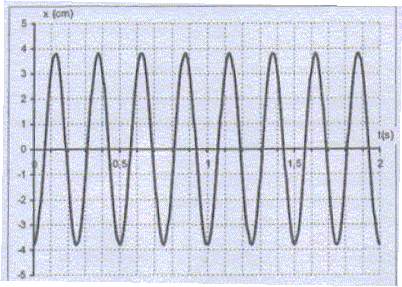La position du centre d'inertie de la masse est repérée sur l'axe horizontal par son abscisse x par rapport à la position d'équilibre. Après l'avoir écartée de sa position d'quilibre, on l'abandonne sans vitesse initiale, et on enregistre la position de G au cours du temps. 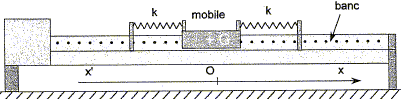Décrire une méthode permettant d'obtenir la courbe ci-dessus. On précisera le matériel nécessaire et on schématisera l'expérience. Le solide de masse m, posé sur un banc à coussin d'air horizontal est attaché à deux ressorts identiques de raideur k. Un capteur de position, non représenté, relié à un dispositif d'acquisition permet d'enregistrer la position du centre d'inertie G du mobile à chaque instant de date t. Cette position est repérée sur un axe x'x horizontal, orienté de gauche à droite. L'origine O coïncide avec la position du centre d'inertie lorsque le mobile est à l'équilibre.   Déterminer l'amplitude et la fréquence. 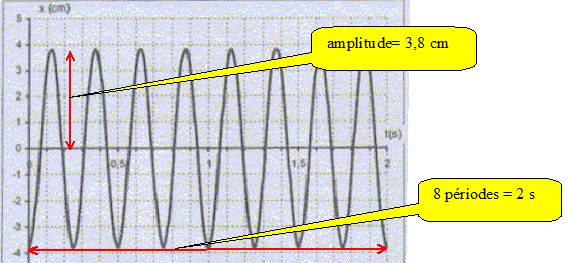T = 2/8 s ; f=1/T = 8/2 = 4 Hz.   Si ce système était relié à une membrane, produirait-il un son audible ? Les fréquences des sons audibles sont comprises entre 20 Hz et 20 000 Hz. Un son de fréquence 4 Hz n'est pas audible. Quelle est la forme de l'équation horaire x(t) du mouvement. x(t) = 3,8 10-2 cos ( 2pf t + p) = 3,8 10-2 cos ( 8p t + p) . A t = 0, x(0) = 3,8 10-2 cos p = -3,8 cm. Les oscillations sont-elles amorties ? Que peut-on en déduire pour le contact entre le solide et le plan ? L'amplitude des oscillations reste constante : pas d'amortissement. Le contact entre le solide et le plan est sans frottement. Montrer que les deux ressorts, de constantes de raideur k1 et k2, se comportent comme un ressort qui travaillerait en allongement comme en compression et dont la constante de raideur serait k=k1+k2 ? Etablir l'équation différentielle du mouvement de G. A position d'équilibre, origine de l'axe : Les tensions ont même valeur : k1(l1éq-l1 0) = k2(l2éq-l2 0) La seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx" -k1(l1-l1 0) + k2(l2-l2 0)= mx" -k1(l1-l1 0) = -k1(l1-l1éq+l1éq-l1 0) ; k2(l2-l2 0) = k2(l2-l2éq+l2éq-l2 0) -k1(l1-l1 0) + k2(l2-l2 0)= -k1(l1-l1éq) +k2(l2-l2éq) ; On note L = l1+l2 =l1éq + l2éq soit : l1-l1éq= l2éq - l2 ; on pose : l1-l1éq=x d'où : -k1x + k2(-x)=mx" : mx"+(k1+k2)x=0. Les deux ressorts, de constantes de raideur k1 et k2, se comportent comme un ressort qui travaillerait en allongement comme en compression et dont la constante de raideur serait k=k1+k2 x" + k/m x=0 ; on pose w²= k/m ; w = 2pf soit f = 1/(2p)[k/m]½ ; T0= 1/f = 2p[k/m]-½ Montrer que l'équation horaire x(t) précédente est solution de cette équation. x'(t) = 0,038 (-w) sin ( wt+p) ; x"(t) = 0,038 (-w2) cos ( wt+p) = - w2 x(t). Repport dans x" + w² x=0 : - w2 x(t)+ w2 x(t)=0 est vérifiée quel que soit t.   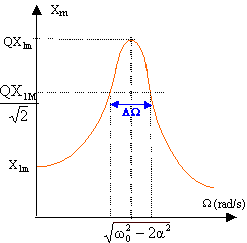Oscillations forcées : On soumet maintenant le système oscillant à une xcitation périodique, semblable à celle engendrée par la bobine du haut parleur. Pour diverses valeurs de fréquences d'excitation, on mesure l'amplitude du mouvement de G. Tracer l'allure de la courbe représentant l'amplitude en fonction de la fréquence, en indiquant la (les) valeur(s)particulière(s). Q : facteur de qualité Q = w0 / (2a) ; a est lié à l'amortissement. valeur maximale d'autant plus grande (résonance aigüe ) que l'amortissement est faible. bande passante : Ensemble de pulsations telles que la valeur de l'amplitude Xm soit supérieure à 0,707 fois la valeur extremale. Quel moyen mécanique peut être utilisé pour produire l'excitation périodique.   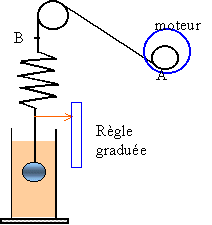La vitesse de rotation du moteur est réglable. Larbre est muni d'un exentrique A. Le point A décrit un cercle de rayon A. Le point B est animé d'un mouvement sinusoïdal d'amplitude a. La fréquence du point B est proportionnelle à la vitesse angulaire du moteur. Le moteur constitue l'excitateur et le pendule vertical est le résonateur. 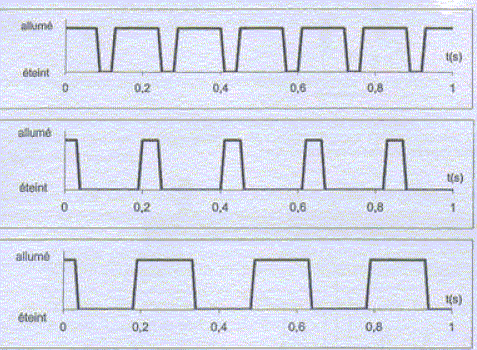On utilise un stroboscope pour mesurer la fréquence de l'excitateur. Des courbes donnant l'éclairement en fonction du temps, de différents stroboscopes, sont données ci-dessous : Quel stroboscope correspond à la meilleure utilisation ? Un stroboscope émet des éclairs de fréquence réglable ; "éclair" : éclairement de courte durée suivie d'une exctinction plus longue : le stroboscope n°2, au centre, est le mieux adapté. Comment déterminer la fréquence d'un phénomène périodique avec un stroboscope. On recherche la plus petite fréquence des éclairs conduisant à l'immobilité apparente. On commence par une fréquence grande et on diminue lentement cette fréquence. 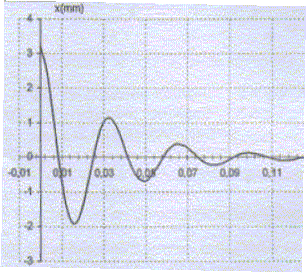Etude du système réel : oscillations libres. Le système informatisé permet d'enregistrer les oscillations du sommet d'un dôme autour de sa position d'équilibre lorsqu'il est abandonné à lui même hors équilibre. 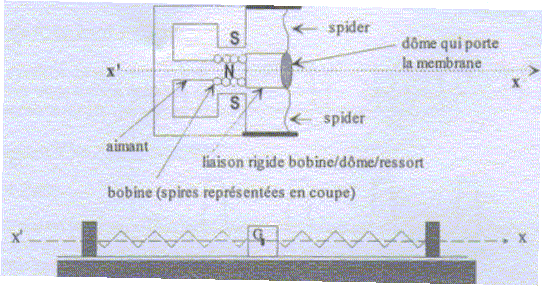On obtient la courbe suivante : Quel est le type d'oscillations que fait apparaître cet enregistrement. Oscillations libres amorties. Quelles sont les raisons prinipales de cette différence avec l'étude du modèle simplifié ? Frottements mécaniques. Calculer la fréquence de ces oscillations. Le son est-il audible ? période T ~0,032 s ; fréquence f = 1/0,032 = 31 Hz, valeur supérieure à 20 Hz, donc son audible. Oscillations forcées : Durant l'utilisation du HP, la vibration de la membrane est le résultat d'une excitation par la bobine placée dans l'entrefer d'un aimant et parcourue par un courant. Quel nom porte la force qui met la bobine en mouvement ? Force de Laplace. D'une manière générale, quel est la nature d'un son ? Onde longitudinale, propagation d'une variation de pression, sans transport de matière, avec transport d'énergie. Le courant circulant dans la bobine doit-il être continu ou variable ? Justifier. Avec un courant continu, la bobine se déplaceraît puis s'arrêterait. Avec un courant variable, la bobine est constamment en déplacement : par l'intermédiaire du dôme, on aura donc l'émission d'une onde sonore. 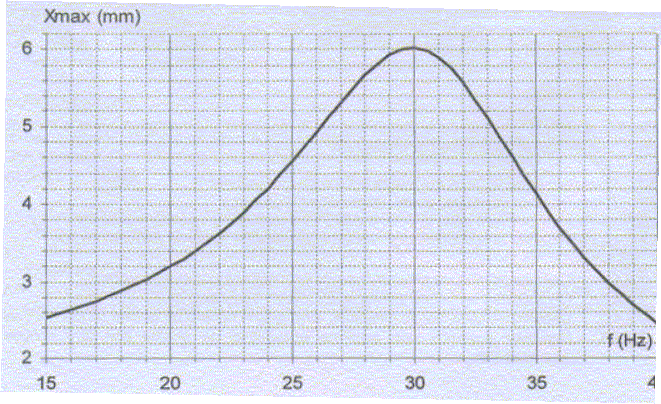On donne la courbe de réponse en fréquence du système oscillant du HP.  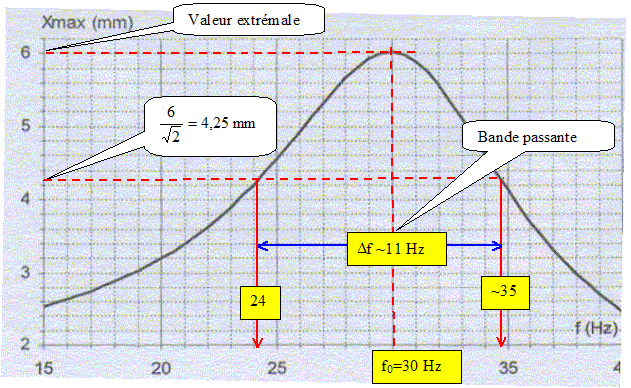Qu'appelle t-on bande passante à - 3dB en fréquence du HP ? bande passante : Ensemble de fréquences telles que la valeur de l'amplitude Xm soit supérieure à 0,707 fois la valeur extremale. Déterminer cette bande passante ainsi que le facteur de qualité de cet oscillateur. Facteur de qualité Q = f0/Df ~30/11~ 3. Expliquer pourquoi une enceinte acoustique de qualité doit être conçue avec plusieurs HP ? Une enceinte acoustique de qualité doit restituer les graves, les médiums et les aigus : la bande passante d'un seul HP n'est pas assez large pour restituer toutes les fréquences d'un son. Il faut utiliser plusieurs HP, l'un pour les graves ; un autre pour les médiums et enfin un 3è pour les aigus.

retour -menu