atmosphère : pression à l'altitude z ; calcul de la constante d'Avogadro concours ITPE 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

L'atmosphère est essentiellement constituée d'un mélange gazeux, l'air. Ce mélange est constitué d'environ 78 % de diazote, de 21 % de dioxygène, moins de 1% d'argon, de 0,03% de dioxyde de carbone et d'une multitude de traces d'autres gaz ( néon, krypton, hélium, ozone, dihydrogène, xénon ). On considère que l'air suit la loi des gaz parfaits : PV = RT pour une mole. On notera r la masse volumique de l'air. Le problème est paramétré par un axe vertical Oz orienté vers le haut. Montrer que la valeur de R est 8,32 SI. Préciser son unité.  Dans les conditions normales de température et de pression ( 1,013 105 Pa et 273,15 K) le volume molaire d'un gaz est 22,4 L = 22,4 10-3 m3. PV = RT donne R = PV/T = 1,013 105*22,4 10-3 / 273,15 = 8,31 J mol-1 K-1. Déterminer, compte tenu de la composition de l'air, que la masse molaire de l'air vaut : M= 29 g/mol. On donne M(Ar)=40 ; M(O) = 16 et M(N)=14. M = 0,78 *28 + 0,21 *32+0,01 *40 = 28,96 = 29 g/mol.   Montrer que l'équilibre hydrostatique peut s'écrire : dP = -rg dz et définir g. 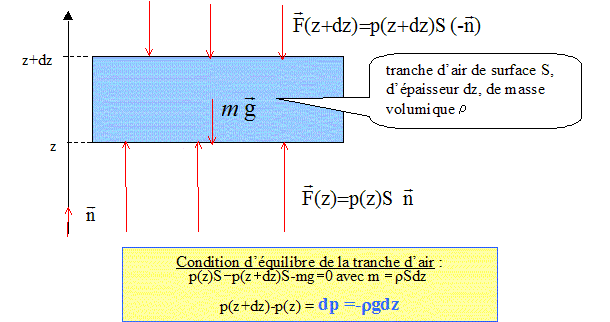g : champ de pesanteur à l'altitude z. On suppose que pour des altitudes comprises entre 11 km et 20 km, la température T de l'atmosphère est constante. On supposera que g garde une valeur constante. Etablir l'expression de la pression à une altitude z : P(z) = K exp(-Mgz/(RT)). équilibre hydrostatique : dp=-rgdz équation des gaz pargaits : p=nRT/V avec n = m/M ( masse / masse molaire) Or m/V = r d'où p= r RT/M soit r = pM/(RT) Par suite : dp = -pMg/(RT) dz dp/p = - Mg/(RT) dz ; d ln p = -Mg/(RT) dz ln p = Mg z /(RT) + Cte à l'altitude zéro, la pression est p0 d'où Cte = ln p0. ln p - ln p0 = -Mg z /(RT) ; ln (p/p0) = -Mg z /(RT) p(z) =p0 exp(-Mgz/(RT)). Préciser la dimension et la signification de la constante K. à l'altitude zéro, la pression est p0     On note n(z) la densité volumique de molécules à l'altitude z. Montrer que l'équation des gaz parfaits s'écrit : P = n(z)kT où k = R/NA est la constante de Boltzmann et NA la constante d'Avogadro. P= nRT/V avec n = N/NA ( N : nombre de molécules) P= NRT / (NAV) = NkT / V avec N/V = n(z) densité volumique de molécules P= n(z) k T. Etablir l'expression de n(z). n(z) = P/(kT) et p(z) =p0 exp(-Mgz/(RT)). n(z) = p0/(kT) exp(-Mgz/(RT)). On pose n(0) = p0/(kT), nombre de particules à l'altitude z=0. n(z) = n(0) exp(-Mgz/ (RT)) Montrer qu'à partir de l'expression de n(z) et de la connaissance de R et m ( masse des particules), on peut déterminer la constante d'Avogadro.  Quantité de matière n = masse totale des particules / masse molaire = nombre de molécules / NA. mtot/M = N/NA donne M= mtotNA/N = masse moyenne d'une particule *NA = m NA. d'où n(z) = n(0) exp [-mNA g z / (RT) ]. On choisit comme origine des altitudes z1. de plus n(z) = nombre de particules / volume = Ni/V : n(z2) / n(z1) = N2/N1. n(z2) = n(z1) exp [-mNA g (z2-z1) / (RT) ]. n(z2) /n(z1) =N2/N1 = exp [-mNA g (z2-z1) / (RT) ] ln(N2/N1) = -mNA g (z2-z1) / (RT) NA = RT ln (N1/N2) / [mg(z2-z1)].    Application numérique : En 1827, Brown, a pour la première fois observé le mouvement d'agitation moléculaire. La répartition dans une colonne verticale à température constante de grains, de masse moyenne m, plongés dans la glycérine suit la loi n(z) établie précédemment. On donne g = 9,81 m s-2, m = 10-14 g, T= 300K. N1 = 560 à l'altitude z1 = 2 mm et N2 = 5 à l'altitude z2 = 2,2 mm Ni : nombre de particules observées. NA = RT ln (N1/N2) / [m g(z2-z1)]. m = 10-17 kg ; z2-z1 = 2,2-2 = 0,2 mm = 2 10-4 m mg(z2-z1) = 10-17 *9,81 *2 10-4 =1,962 10-20. NA = 8,32*300 ln (560/5) / 1,962 10-20 = 6,0 1023.

retour -menu