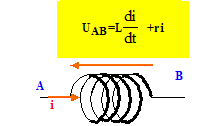|
Etude de quelques montages inductifs, filtre passe haut, diagramme de Bode concours Mines 03 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||
| .
. |
|||||||||
|
|||||||||
|
La bobine est dite parfaite si sa résistance interne est négligeable. Donner la relation entre le courant i qui traverse une bobine parfaite et la tension uL à ses bornes (on précisera à l’aide d’un schéma les conventions d’orientation adoptées pour i et uL).
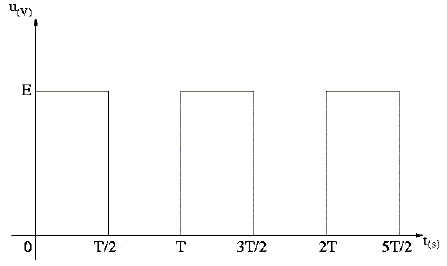
Les valeurs usuelles des inductances rencontrées s’échelonnent de quelques henrys à quelques millihenrys. On se propose d’étudier la réponse d’un circuit (RL) à une tension en créneaux délivrée par un générateur basse fréquence (G.B.F.).
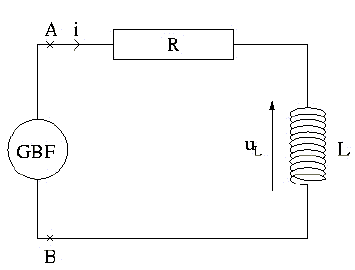
Le circuit représenté sur la figure comporte une bobine parfaite d’inductance L, une résistance R et un G.B.F délivrant une tension en créneaux u représentée.
On définit la constante de temps t, exprimée en secondes, du circuit (RL) par une relation du type t = La.Rb ou a et b sont deux constantes réelles. Par analyse dimensionnelle rapide, déterminer la valeur des exposants a et b (on raisonnera à partir des caractéristiques entre u et i).
Ejoule = RI2t ; R :
énergie /
(intensité2.temps) t : temps. L/R a la dimension d'un temps. t
= L/R ; a
=1 ;
b
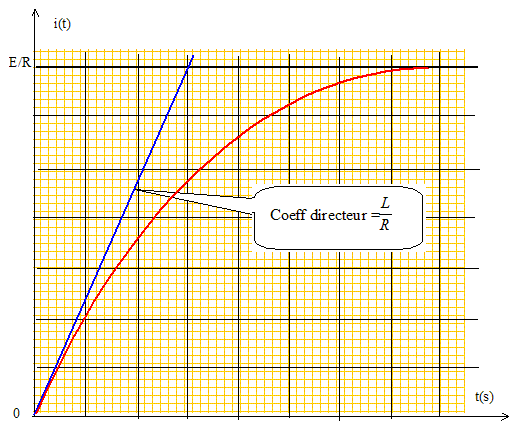
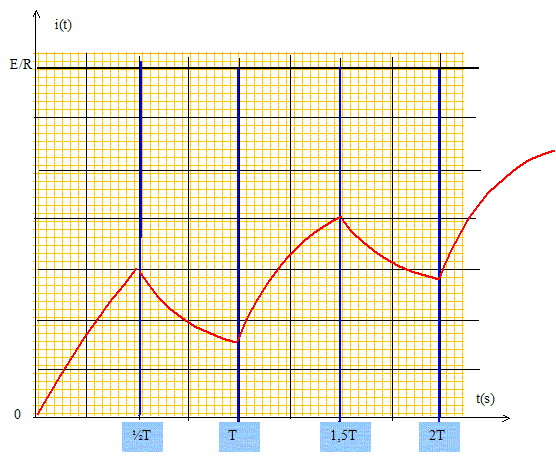
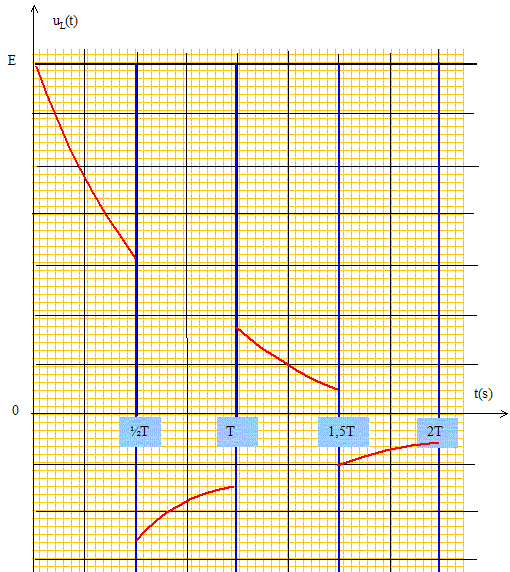
=-1. L'intégrer en justifiant soigneusement la détermination de la (des) constante(s) d'intégration. uL+ Ri = E ; Ldi/dt +Ri = E.(1) solution générale de l'équation sans second membre : i(t) = A exp(-t/t). solution particulière de (1), régime permanent : i= E/R. solution générale de (1) : i(t) = A exp(-t/t) +E/R. à t=0, l'intensité est nulle : 0 =A+E/R ; A= -E/R. i(t) = E/R[1- exp(-t/t)]. En déduire l'expression de uL(t). uL=Ldi/dt = LE/(Rt) exp(-t/t) ; uL= E exp(-t/t). Tracer l'allure des courbes représentatives de i(t) et de uL(t) en précisant les valeurs vers lesquelles ces fonctions tendent en régime permanent, ainsi que les pentes des tangentes à l'origine.
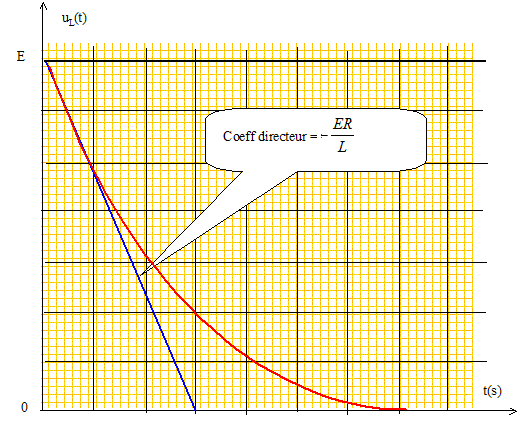
Déterminer complètement l'expression de i(t) et de uL(t) pour ½T < t < T. uL+ Ri = 0 ; Ldi/dt +Ri = 0.(2) solution générale de l'équation différentielle : i(t) = A exp(-t/t). continuité de l'intensité ; à t = ½T : A exp(-½T/t) = E/R- E/Rexp(-½T/t) ; A= E/R exp(½T/t) -E/R= E/R[exp(½T/t)-1]. i(t) =E/R[exp(½T/t)-1]exp(-t/t). uL=Ldi/dt = LE/(Rt)[exp(½T/t)-1] exp(-t/t) ; uL= E[exp(½T/t)-1] exp(-t/t).
Le G.B.F. est réglé sur la fréquence f = 1,0 kHz, la bobine a pour inductance L = 1,0 H et R = 1,0.103 W. Comparer la période T de la tension délivrée par le G.B.F. et la constante de temps t du circuit. T = 1/f = 10-3 s = 1 ms ; t = L/R = 10-3 s = 1 ms. Tracer qualitativement l'évolution des graphes de i(t) et uL(t) sur quelques périodes.
Dans le circuit ci-dessus, le G.B.F. est à présent en mode sinusoïdal. En utilisant les analogies transitoire-alternatif écrire, à partir de l’équation différentielle établie, la loi d’Ohm complexe liant les amplitudes complexes U et I respectivement de la tension aux bornes du dipôle AB et de l’intensité du courant le traversant. Ldi/dt +Ri = uAB.(1) à la dérivée d/dt correspond jw d'où : jwLI + R I = U ; (jwL +R) I = U. En déduire l’impédance complexe Z du dipôle AB. Z= (jwL +R)
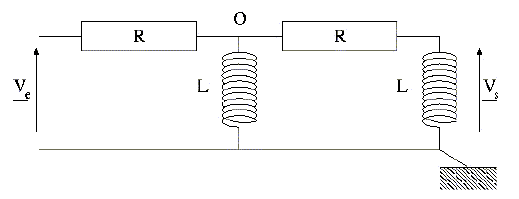
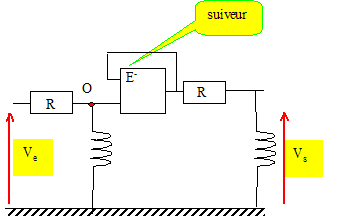
On s'interesse au quadripole ci-dessous, constitué de deux cellules (RL) enchainées, alimenté par une tension sinusoidale de pulsation w.
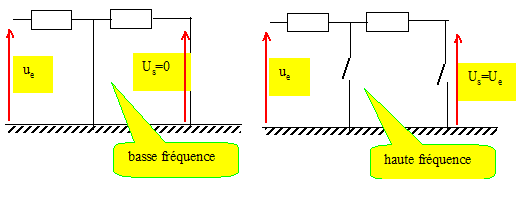
En étudiant le comportement asymptotique du quadripôle aux hautes et basses fréquences, préciser la nature du filtre ainsi constitué.
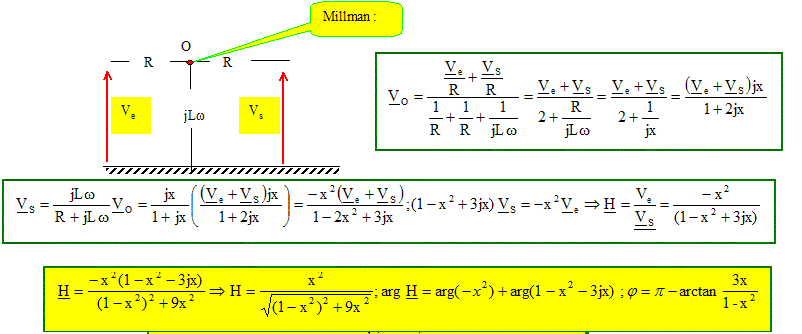
Filtre passe haut. Déterminer la fonction de transfert H( jx) de ce quadripole en fonction de x =Lw/R, après avoir précisé la dimension de x. Lw et R sont des impédances en ohm ; Lw/R est sans dimension.
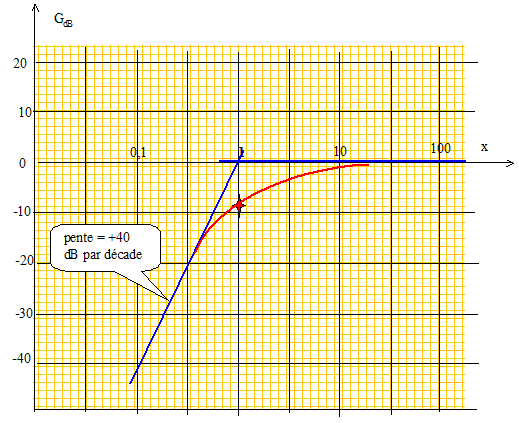
Tracer le diagramme de Bode asymptotique de ce filtre, en le justifiant. gDB= 20 log H = 40 log x -10 log((1-x2)2+9x2] Si x tend vers 0, gdB est équivalent à : 40 log x drpote de pente 40 dB par décade. Si x = 1; gdB= -10 log 9 = -9,5 dB. Si x tend vers l'infini, H tend vers 1 et gdB tend vers 0, asymptote horizontale.
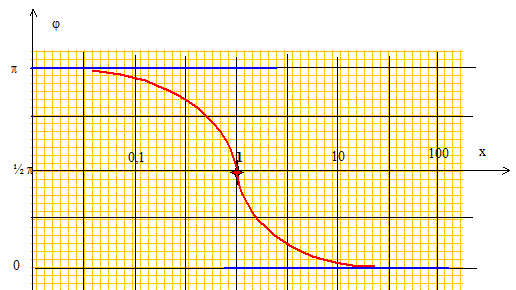
j =p-arctan [3x /(1-x2)]. si x tend vers zéro, j tend vers p ; si x tend vers 1, j tend vers ½p ; si x tend vers l'infini, j tend vers 0.
Comment modifier le montage pour obtenir un filtre dont la fonction de transfert s'écrirait comme le carré de la fonction de transfert d'un filtre (RL) ? |
|||||||||
|
|
|||||||||
|
|