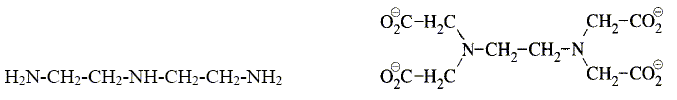|
Composés azotés, EDTA, cinétique chimique concours Mines 06 sans calculatrice. En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
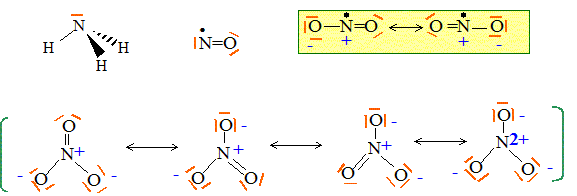
Le numéro atomique de l’azote est Z = 7. Celui de l’oxygène est Z = 8. Donner la configuration électronique de l’atome d’azote et indiquer sa place dans la classification périodique. 1s2 2s2 2p3. ( 2è ligne ; 5è colonne de la classification simplifiée ou 15è colonne de la classification complète) Donner une ou plusieurs représentations de Lewis pour chacun des composés suivants : NH3, NO, NO2, NO3-.
Que vaut l’angle entre 2 liaisons NO dans l’ion nitrate NO3- ? Les 3 liaisons NO ont-elles même longueur ? Justifier. Du fait des formules mésomères, les trois angles sont égaux à 120 ° et les trois liaisons sont égales. Comment peut-on expliquer que NO2 soit en équilibre avec N2O4 à température ambiante selon 2 NO2 = N2O4 ? (1) La présence d'un électron célibataire sur l'azote fait que NO peut se dimériser. Les enthalpies standard de formation de NO2 et N2O4 valent respectivement 33,4 et 12,5 kJ.mol-1. En déduire si la réaction (1) est endo- ou exothermique. DrH° = DfH° (N2O4)-2 DfH° (NO2) =12,5-2*33,4 = -54,3 kJ mol-1, valeur négative donc exothermique. Donner les nombres d’oxydation de l’élément azote dans les composés NO, NO3- et N2O4. NO : n.o(N) = +II ; NO3- : n.o(N) +3 n.o(O)=-1 ; n.o(N) +3(-2)=-1 ; n.o(N) = +V N2O4 2n.o(N) +4 n.o(O)=0 ; 2n.o(N) +4(-2) = 0 ; n.o(N)=+IV. L’une des étapes de la synthèse de l’acide nitrique est l’hydrolyse de N2O4. Ecrire l’équation de la réaction correspondante sachant qu’elle conduit à la formation de NO3- et NO. 3N2O4 + 2H2O = 2NO + 4NO3-+ 4H+. Les gaz dd’échappement sortant des voitures contiennent des oxydes d’azote toxiques pour l’environnement. Quel moyen technique a été trouvé pour réduire le problème ? utilisation de pot d'échappement catalytique. Solutions aqueuses. La diéthylènetriamine (notée dien) et l’ion éthylènediaminetétraacétate (noté Y4-) sont des composés azotés utilisés en analyse quantitative. Leurs formules respectives sont données ci-dessous.
Ce sont des bases, et des agents complexants. Parmi les adjectifs suivants, préciser, en justifiant la réponse, celui qui s'applique à chacun des composés : monodenté, bidenté, tridenté, tétradenté, hexadenté. La diéthylènetriamine est tridenté : 3 atomes d'azote possédant chacun un doublet libre. L’ion éthylènediaminetétraacétate est hexadenté : 2 atomes d'azote et 4 atomes d'oxygène possédant chacun un doublet libre. L’ion Y4- est utilisé en travaux pratiques pour titrer les cations métalliques Mg2+ et Ca2+ présents dans les eaux minérales. Écrire l’équation de la réaction de titrage correspondante pour l’un des 2 cations. Mg2++ Y4- = MgY2-.
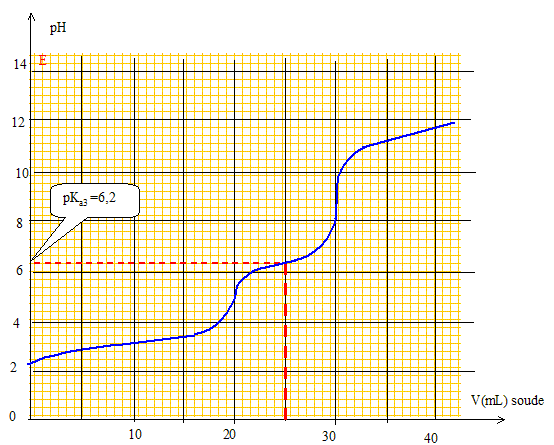
Quelles électrodes utiliseriez-vous pour suivre ce titrage par pH-métrie ? Préciser leurs rôles respectifs. Electrode combinée. ou bien électrode de verre ( pour la mesure du pH) et une électrode au calomel saturée ( référence). Pour quels volumes de soude versée devrait-on a priori observer des sauts de pH si l’on considère les titrages comme successifs? Justifier. A l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoechiométriques. 1ère équivalence : CaVa = CbVb soit Vb= CaVa /Cb = 10-2*10/10-2 = 10 mL. 2ème équivalence : 20 mL ; 3ème équivalence : 30 mL ; 4ème équivalence : 40 mL. Certains de ces sauts de pH ne sont pas observés expérimentalement ? Lesquels et pourquoi ? Les deux premiers pKa sont proches l'un de l'autre : le premier saut de pH n'est pas observé. Le dernier pKa est trop élevé : le dernier saut de pH n'est pas observé. Tracer l’allure de la courbe de titrage pH = f(v), où v désigne le volume de soude versé. Préciser sur la courbe les volumes correspondant aux sauts de pH ainsi que le pKa le plus accessible expérimentalement.
On note dans cette partie EDTA l'ensemble des formes acido-basiques de l'acide éthylènediaminetétraacétique (depuis H4Y jusqu'a Y4-). [EDTA] désigne donc la somme des concentrations de toutes les espèces précédentes. Les ions Cu2+ forment des complexes avec la diéthylènetriamine (notée dien) et avec la forme ionique Y4- de l'EDTA. On se propose d'étudier la vitesse de la réaction : Cu(dien)2+ + EDTA = CuY2- + dien. Le tableau suivant résume les conditions expérimentales et les résultats d'une mesure de la concentration C en Cu(dien)2+ au cours du temps dans les conditions suivantes : q = 25�°C ; pH = 4,0 maintenu constant. concentrations initiales : [Cu(dien)2+]0 = 2,00.10-3 mol.L-1 ; [EDTA]0 = 6,00.10-2 mol.L-1.
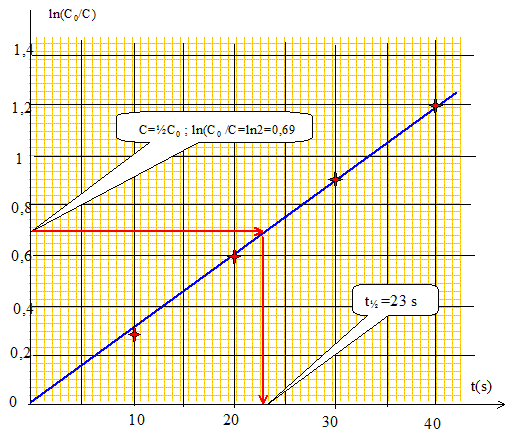
Donner l'expression de la vitesse de la réaction, en supposant qu'elle admet un ordre a par rapport à Cu(dien)2+ et b par rapport à EDTA. v = k[Cu(dien)2+]a [EDTA]b. Montrer sans calcul que les conditions initiales choisies permettront de déterminer l'un des ordres partiels. En déduire l'expression de la constante apparente de vitesse kapp. [EDTA]0 est 30 fois supérieure à [Cu(dien)2+]0 : [EDTA] peut être considérée comme constante. kapp = k[EDTA]0b ; v = kapp [Cu(dien)2+]a Déterminer graphiquement l'ordre partiel de la réaction par rapport à Cu(dien)2+? Hypothèse : a =1. On note [Cu(dien)2+]0 =C0 et [Cu(dien)2+]t =C. v = dC/dt = -kappC ; dC /C = -kapp dt ; d ln(C) = - kapp dt. ln(C)= -kapp t + Cte ; à t =0, C=C0 d'où : Cte = lnC0 ; ln(C) - lnC0 = -kapp t. ln(C0 /C) = kapp t.
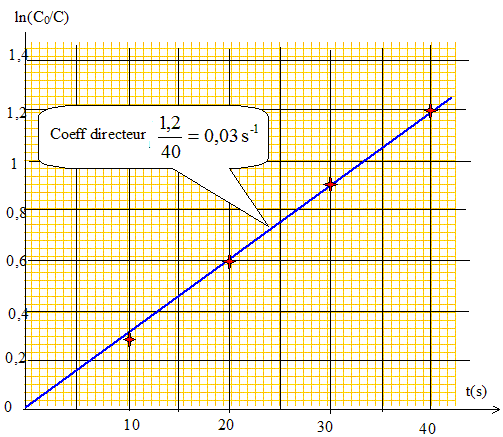
Le graphe est une droite : l'hypothèse a=1 est vérifiée. Calculer la constante apparente de vitesse kapp et déterminer le temps de demi-reaction t1/2. On donne Ln 10= 2,30 et Ln 2= 0,69. kapp =3,0 10-2 s-1 ; t½ =ln2 /kapp = 0,69 / 0,03 = 23 s.
Des mesures analogues ont conduit aux résultats suivants :
Le produit [EDTA]0.t½ étant constant, l'ordre partiel par rapport à l'EDTA est b=1 On étudie maintenant l'influence du pH sur la vitesse de la réaction. Le tableau suivant donne la constante de vitesse kapp en fonction du pH dans des conditions qui sont précisées: q = 25�°C ; concentrations initiales : [Cu(dien)2+]0 = 2,00.10-3 mol.L-1 ; [EDTA]0 = 1,00.10-2 mol.L-1.
exprimer les concentrations de ces deux espèces en fonction de [EDTA]0, Ka3 et h = [H3O+]. (On précise que Ka3 est la constante d'acidité du couple (H2Y2-/ HY3- )). H2Y2-+ H2O = HY3- +H3O+. Ka3 = [HY3-][H3O+] /[H2Y2-] = [HY3-]h /[H2Y2-] soit : [HY3-] /[H2Y2-] =Ka3 /h. Conservation de l'EDTA : [EDTA]0 =[HY3-] +[H2Y2-] =[H2Y2-] [ [HY3-] /[H2Y2-] +1]. [H2Y2-] =[EDTA]0 / [ Ka3 /h +1] [EDTA]0 =[HY3-] [[H2Y2-] /[HY3-] +1] ; [HY3-] =[EDTA]0 / [ h/Ka3 +1]
Exprimer kapp en fonction de h, de [EDTA]0, de k1, k2 et Ka3. kapp =[EDTA]0 [ k2/ [ Ka3 /h +1] + k1 / [ h/Ka3 +1] ] Montrer que dans l'intervalle de pH de l'expérience h>>Ka3. Ka3 = 10-6,2 =6,3 10-7. intervalle d'étude : 10-3,5 >h >10-4,9 ; 3,2 10-4> h>1,3 10-5. Donc h >>Ka3. En déduire que kapp peut se mettre sous la forme kapp =A+B/h, où A et B seront exprimés en fonction de constantes que l’on précisera. kapp =[EDTA]0 [ k2/ [ Ka3 /h +1] + k1 / [ h/Ka3 +1] ] h >>Ka3 donc Ka3 /h <<1 et h/Ka3 >>1 d'où : kapp =[EDTA]0 [ k2 + k1Ka3 / h] A = [EDTA]0 k2 ; B = [EDTA]0 k1Ka3 Expliquer alors comment on pourrait accéder à k1 et k2 à partir des données expérimentales. Tracer kapp en fonction de 1/h : droite de coefficient directeur B et d'ordonnée à l'origine A. De plus [EDTA]0 et Ka3 sont connus. La mise en oeuvre de la méthode proposée ci-dessus conduit à k1 = 20,0 L.mol-1.s-1 et k2 = 0,43 L.mol-1.s-1. Quelle est la forme la plus réactive de l'EDTA vis à vis de Cu(Dien)2+? k1 est très supérieur à k2 donc HY3- est la forme la plus réactive. Pourquoi ne fait-on pas intervenir les termes k4 [H4Y], k3 [H3Y-] et ko [Y4-] dans l'expression de kapp ? (On pourra tenir compte, entre autre, de la charge des espèces considérées pour répondre à ces questions.) Cu(dien)2+ porte deux charges positives : il a plus d'affinité pour une espèce fortement chargée, HY3-, même si celle-ci est minoritaire dans le domaine de pH considéré. De plus, dans le domaine de pH de l'étude H4Y et Y4- sont ultraminoritaires. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|