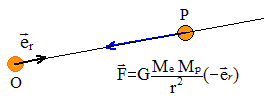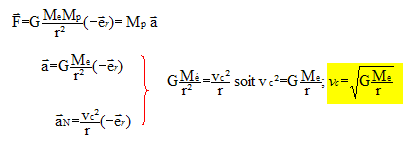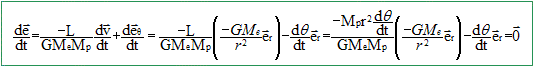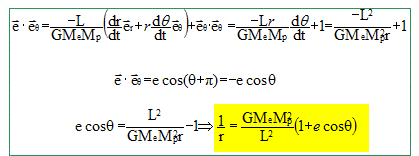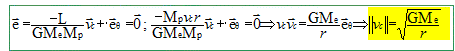|
Mouvement d'une planète concours Mines 07 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
Nous voulons étudier le mouvement d'une planète, assimilée à un point matériel dans le champ de gravitation d'une étoile de masse Me de centre O, considérée comme ponctuelle et fixe. La planète de masse Mp est située à une distance r=OP de O. Nous considérerons un référentiel lié à l'étoile comme un référentiel galiléen. Exprimer la force exercée par l'étoile sur la planète en fonction des masses Me et Mp, r, G, la constante universelle de gravitation et le vecteur unitaire er = OP/r.
Justifier précisément que le mouvement est plan. Préciser ce plan. Ecrire le théorème du moment
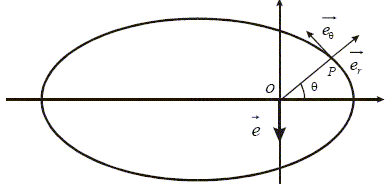
cinétique en O : La trajectoire est plane : ce plan contient le point O et le vecteur force F. Ce plan est perpendiculaire au moment cinétique L. On notera (er et eq). la base de projection dans ce plan et ez, un vecteur unitaire suivant la direction du moment cinétique en O, L= Lez. Rappeler l’expression de la vitesse en coordonnées polaires.
Préciser l'expression de en fonction de L en fonction de Mp, r, dq/dt.
Etablir l'expression de la vitesse vc de la planète, en fonction de R,G et Me.
En déduire une relation entre r, T, G et Me ( 3ème loi de Képler). La période est la durée nécessaire pour décrire une circonférence de rayon r : T = 2pr/vc. T2 = 4 p2 r2/vc2 = 4 p2 r3/ (GMe) ; T2 / r3 =4 p2 / (GMe).
On rappelle que l'équation polaire d’une ellipse est
Montrer que ce vecteur est constant. Il suffira de montrer que la dérivée de ce vecteur est nulle.
En faisant le produit scalaire e. eq et en s’aidant du dessin, montrer que r(q)=p/[1+ecos(q)] et en déduire que le module de e vaut l'excentricité e de la trajectoire. Préciser p en fonction de G, Me, Mp et L.
p = L2/(GMeMp2) Préciser la valeur de l’excentricité pour un mouvement circulaire. L'excentricité est nulle dans le cas d'un mouvement circulaire. Dans le cas d’un mouvement circulaire, préciser la valeur de L en fonction de r, vc et Mp. L = Mp vcr Retrouver à l’aide du vecteur excentricité, l'expression de la vitesse de la planète, en fonction de r, G et Me.
|
|||||||
|
|
|||||||
|
|