Circuit RLC série, détecteur de niveau de pH ( bac Stl chimie de laboratoire 2009)

. .

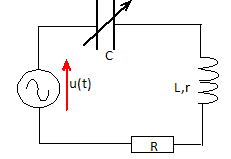
Circuit RLC série. On dispose d'un générateur basse fréquence délivrant la tension alternative sinusoïdale u(t) de pulsation w = 3000 rad/s. Déterminer la fréquence et la période de ce signal. Fréquence f = w /(2 pi) = 3000 /(2*3,14) = 4,7746 102 ~ 477 Hz. Période : T = 2 pi / w = 2*3,14 / 3000 = 2,094 10-3 ~2,09 10-3 s. A l'aide de ce générateur, on alimente le circuit série constitué d'un résistor de résistance R, d'une bobine réelle d'inductance L et de résistance r, et d'un condensateur de capacité variable C. Dessiner le circuit décrit ci-dessus. 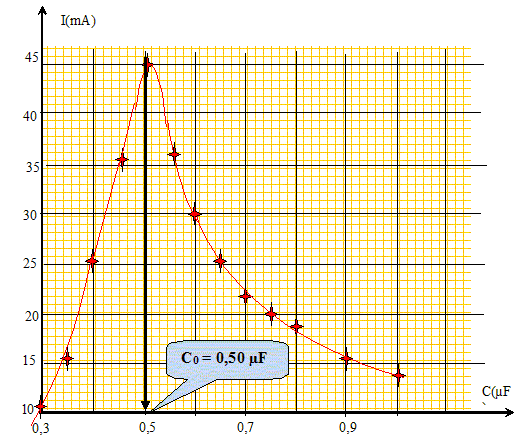Donner la relation entre L, C, w à la résonance d'intensité. LCw2=1. Rappeler l'expression littérale de l'impédance de ce circuit lorsqu'il est à la résonance d'intensité. L'impédance est minimale à la résonance d'intensité, égale à la résistance totale du circuit : Z = (R+r). Le générateur délivre une tension u(t) de valeur efficace U = 5,0 V et de pulsation w = 3000 rad/s. Pour différentes valeurs de la capacité du condensateur, on mesure la valeur efficace I de l'intensité du courant. A partir du tableau de valeurs ci-dessous, tracer la courbe représentative des valeurs de I en fonction des valeurs de C. Déduire la valeur C0 de la capacité du condensateur à la résonance. C ( µF ) 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 I(mA) 1,9 3,2 4,9 7,5 10,9 16,5 24,9 36,2 45,1 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1,00 36,5 30,2 25,1 22,1 19,5 18,0 16,5 15,8 14,7 14,1 En déduire la valeur L de l'inductance de la bobine. 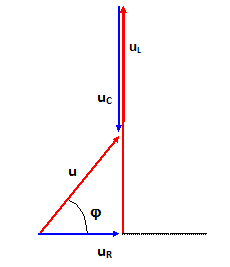L=1/ (C0w2)= 1/(0,50 10-6 * 30002) =0,222 ~ 0,22 H. Sachant que R = 100 ohms, déterminer la résistance r de la bobine. A la résonance d'intensité, U = (R+r) I ; r = U/I-R = 5,0 / (45,1 10-3) -100 = 10,86 ~ 11 ohms. Un voltmètre, en position AC, branché successivement aux bornes de la bobine et du condensateur indique la même valeur lors des deux mesures : 27,3 V. Quelle grandeur le voltmètre fournit-il ? Le volmètre donne la tension efficace. Déterminer le coefficient de surtension. 27,3 / 5 = 5,46 ~5,5. Lorsque C = 0,80 µF, les valeurs efficaces suivantes des tensions mesurées aux ornes des différents dipôles sont : aux bornes du résistor uR = 1,7 V ; aux bornes de la bobine uL =11,8 V, aux bornes du condensateur uC = 7,3 V. En considérant la bobine comme parfaite et en prenant l'intensité i(t) comme référence, construire les vecteurs de Fresnel associées aux tensions uL(t), uR(t) et uC(t). En déduire le vecteur de Fresnel associé à u(t) et le déphasage j de la tension aux bornes du circuit par rapport à l'intensité. u2 = (uL-uC)2 + uR2 ; u = [ (uL-uC)2 + uR2 ]½ = [ (11,8-7,3)2 -1,72 ]½ =23,14½ =4,8 V. tan j = (uL-uC) / uR = 4,5 / 1,7 = 2,647 ; j =69,3 ~ 69 °. Détecteur de niveau de pH. 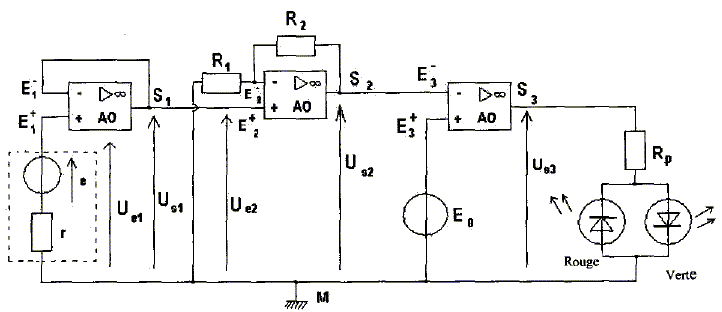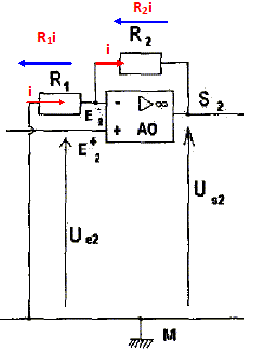Le montage est constitué de : - trois amplificateurs opérationnels (AO) idéaux, dont les valeurs des tensions de saturation sont +/- 14 V - deux DEL supposées parfaites, l'une verte (V), l'autre rouge ( R) - d'un générateur délivrant la tension continue E0 comprise entre 0 et 10 V - d'une électrode combinée qui constitue une pile de résistance interne r et de fem telle que : e = -0,058 pH + 0,406 (V). Rappeler les proprités d'un AO idéal fonctionnant en régime linéaire. Les intensités des courants d'entrée sont nulles i+ = i- = 0. Les deux entrées sont au même potentiel VE+ = VE-. Montrer que US1 = Ue1 = e. L'amplificateur n°1 ( situé à gauche ) fonctionne en régime linéaire : un fil de connexion relie la sortie s1 à l'entrée inverseuse e-1 . Il constitue un montage suiveur. L'AO 2 est monté en amplificateur non inverseur. Etablir la relation entre US2 et e. Faire un schéma en y indiquant les courants et les tensions nécessaires au calcul. Additivité des tensions : UE2 = US2 +R2i et UE2 =-R1 i et UE2 = US1 = e d'où i = -e / R1. e = US2 - R2 e / R1 ; US2 = e +R2 e / R1 ; US2 = (R1 +R2 ) e / R1. Quelle valeur doit-on donner à R2 pour que US2 ~ 10 e ? On donne R1 = 1,0 kW. (R1 +R2 ) / R1 = 10 ; R2 = 9,0 kW. Quel est le régime de fonctionnement de l'AO 3 ? En déduire le nom du montage réalisé avec l'AO 3 ? Il n'y a pas de liaison entre la sortie S3 et l'entrée inverseuse E-3 : l'AO 3 ne fonctionne pas en régime linéaire mais en rgime de saturation. C'est un montage comparateur. Quelle est la valeur de la tension US3 : - lorsque E0 > US2 ? Si E+3 > E-3 alors US3 = + Vsat = + 14 V ; or E+3 = E0 et E-3 = US2 Si E0 > US2 alors US3 = + Vsat = + 14 V ; - lorsque E0 < US2 ? Si E+3< E-3 alors US3 = - Vsat = - 14 V ; or E+3 = E0 et E-3 = US2 Si E0 < US2 alors US3 = - Vsat = - 14 V. On plonge l'électrode dans une solution de pH = 3,0. la tension délivrée par le générateur de tension continue a pour valeur E0 = 4,0 V. On rappelle que US2 = 10 e. Quelle est la diode allumée ? Justifier. e = -0,058 pH + 0,406 = -0,058 *3 + 0,406 =0,23 V ; US2 = 10 e = 2,3 V Si E0 > US2 alors US3 = + Vsat = + 14 V ; la diode verte est passante. On impose E0 = 1,0 V. Déterminer la valeur du pH pour laquelle le système bascule. Le système bascule si E0 = US2 = 10 e =10 (-0,058 pH + 0,406) E0 = -0,58 pH + 4,06 ; pH =(4,06- E0 ) / 0,58 = (4,06-1,0) / 0,58 = 5,3.

retour -menu