|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||
|
||||||||||||||||
|
Toute réponse doit être accompagnée de justifications ou de commentaires. À chaque affirmation, répondre par VRAI ou FAUX, en justifiant le choix à l'aide de définitions, de schémas, de calculs… Si l'affirmation est fausse donner la réponse juste. Les réponses fausses ne sont pas pénalisées par un retrait de point. A : Une onde transversale se propage le long d'une corde dont l'extrémité est fixe (figure 1a).
Affirmation 1 : après réflexion sur l'extrémité fixe de la corde, l'onde repart comme indiqué sur la figure 1b. L'extrémité de la corde est fixe. A cette extrémité se superpose l'onde incidente( d'amplitude A) et l'onde réfléchie : l'amplitude de l'onde réfléchie doit être l'opposé de l'amplitude de l'onde incidente.
L'affirmation 1 est donc fausse. B : une corde métallique est tendue entre deux points fixes A et B distants de AB = D = 40 cm (figure 2). On réalise une excitation sinusoïdale de la corde à l'aide d'un aimant et d'un GBF dont la fréquence est réglée sur 220 Hz. On rappelle que la
célérité d'une onde se propageant le
long d'une corde tendue est donnée par la relation
:
Dans les conditions de l'expérience décrite sur la figure 2, le son émit par la corde est audible à grande distance. Le son émis, de fréquence 220 Hz, fait partie des sons audibles ; son amplitude est faible. Les extrémités d'une corde placée dans un piano, sont reliées à une caisse de résonance en bois. La caissse de résonance permet d'augmenter le niveau sonore du son. Celui-ci peut alors être audible à " grande distance". L'affirmation 2 est donc fausse. Affirmation 3 : le mode de vibration observé sur la figure 2 est le mode fondamental. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. Pour le mode de vibration fondamental : n =1 ; cela correspond à un seul fuseau. L'affirmation 3 est donc vraie. Affirmation 4 : le point A est un ventre de vibration. Le point A, extrémité fixe de la corde tendue, a une amplitude de vibration nulle : c'est un noeud de vibration. L'affirmation 4 est donc fausse. Affirmation 5 : Si on diminue la longueur de la corde en remontant le plateau percé B, on observe un seul fuseau d'amplitude plus grande. La corde ne change pas ; sa tension reste la même : la célérité c du son est donc inchangée. La fréquence f du GBF est également inchangée. Or l = c/f : la longueur d'onde ne change pas. Par contre la longueur de la corde diminue. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. L= ½nl avec n = 1 pour le fondamental. Si L diminue, l'égalité est satisfaite si n diminue ( l étant constante) : cela est impossible. Les ondes stationaires ne peuvent pas s'établir. L'affirmation 5 est donc fausse.
Affirmation 6 : L'onde stationnaire observée sur la figure 2 a une longueur d'onde l = 80 cm. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. n = 1 pour le fondamental : l = 2L = 2*40 = 80 cm. L'affirmation 6 est donc vraie. Affirmation 7 : Sans changer la masse m, on peut observer deux fuseaux en réglant la fréquence du GBF sur 110 Hz. La corde ne change pas ; sa tension reste la même : la célérité c du son est donc inchangée. La fréquence f du GBF est divisée par deux. Or l = c/f : la longueur d'onde double. La longueur de la corde reste constante. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. L= constante ; or la longueur d'onde double : n doit donc être divisé par deux et n doit être entier. La valeur initiale de n étant 1, on ne peut pas obtenir un nombre entier par division. Dans les mêmes conditions, si la fréquence double, la longueur d'onde est divisée par deux. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. L= constante ; la longueur d'onde étant divisée par 2, n doit donc doubler ( observation de deux fuseaux). L'affirmation 7 est donc fausse. Affirmation 8 : En réglant à nouveau la fréquence du générateur sur 220 Hz, on peut observer deux fuseaux en remplaçant la masse m par une masse m' = m/4. La tension de la même corde est divisée par 4 : la célérité c est donc divisée par 2. La fréquence du GBF est inchangée. Or l = c/f : la longueur d'onde est divisée par 2. Condition d'existence d'ondes stationnaires entre deux obstacles fixes séparés par une longueur L : 2L= nl avec n entier. L= constante ; la longueur d'onde étant divisée par 2, n doit donc doubler ( observation de deux fuseaux). L'affirmation 8 est donc vraie.
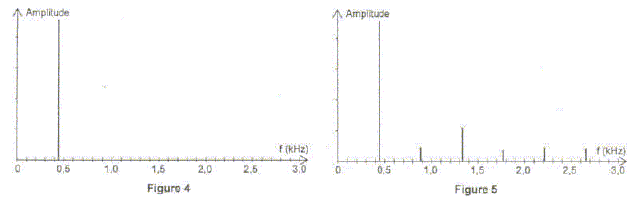
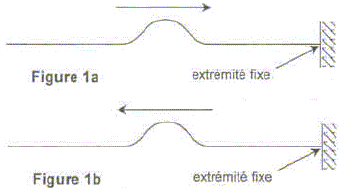
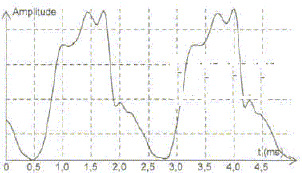
Affirmation 11 : Le son enregistré sur la figure 3 a pour fréquence du fondamental f = 4,4 102 Hz.
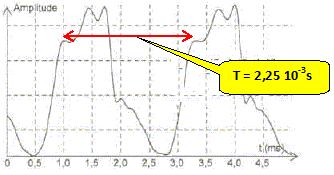
f = 1/ (2,25 10-3 )= 4,4 102 Hz L'affirmation 11 est donc vraie. Affirmation 12 : Le spectre de la figure 4 correspond à l'enregistrement de la figure 3. figure 4 : i l s'agit d'un son pur ( absence d'harmoniques) figure 3 : la courbe n'est pas une sinusoïde, il s'agit donc d'un son complexe. L'affirmation 12 est donc fausse. Affirmation 13 : Les spectres des figures 4 et 5 correspondent à des notes de même hauteur. La fréquence du fondamental correspond à la hauteur d'une note. Sur ces deux spectres, la fréquence du fondamental est identique ( proche de 0,5 kHz). L'affirmation 13 est donc vraie. Affirmation 14 : Les spectres des figures 4 et 5 correspondent à des notes jouées par le même instrument. figure 4 : i l s'agit d'un son pur ( absence d'harmoniques) figure 5 : présence d'harmoniques, il s'agit donc d'un son complexe. La hauteur des notes est la même, la composition des harmoniques est différente : il s'agit de la même note jouée par deux instruments différents. L'affirmation 14 est donc fausse.
|
||||||||||||||||
|
|
||||||||||||||||
|
|

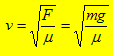 dans le cas présent, µ étant la masse
linéique de la corde.
dans le cas présent, µ étant la masse
linéique de la corde.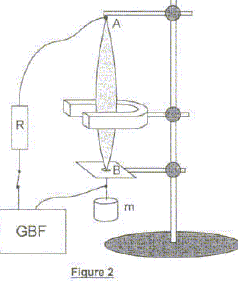
 figure
3
figure
3