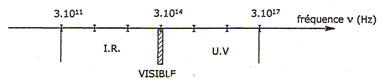Spectrophotométrie : dispersion, diffraction, interférences concours Capes interne 2009 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Un rayonnement électromagnétique monochromatique est une onde qui se caractérise au niveau temporel par sa fréquence n ou sa pusation w. w = 2 p n, fréquence en hertz (Hz) et pulsation en rad s-1. La longueur d'onde l est la distance (m) parcourue par le front d'onde durant une période (T = 1 /n) à la célérité v ( m/s). La longueur d'onde dans le vide est noté l0, et l dans un milieu d'indice n. l0 = c /n, avec c : célérité de la lumière dans le vide. l = v /n et n = c/v d'où l0 = n l. Un rayonnement électromagnétique peut être également considéré comme un flux de corpuscules élémentaires appelés photons. On associe à chacun de ces photons un énergie E = h n, avec h la constante de Plank. ( prix Nobel pour ces travaux sur ce thème en 1918 ). A partir de l'échelle en fréquence des rayonnements électromagnétiques s'étendant de l'UV et jusqu'à l'IR, établir les échelles correspondantes : - en longueur d'onde dans le vide n(Hz) 3 1011 3 1014 3 1017 l0 = c /n (m) 3 108 / 3 1011 = 10-3 10-6 10-9 E = h n (eV) 1,24 10-3 1,24 1,24 103 - en énergie de photons ( eV) : E = h n = 6,62 10-34 *3 1011 =1,986 10-22 J 1,986 10-22 /1,60 10-19 = 1,24 10-3 eV On donne h = 6,62 10-34 J s ; e = 1,60 10-19 C ; c= 3,00 108 m/s. On considère une espèce chimique possédant deux niveaux d'énergie discrets E1 et E2 avec E2 > E1. Quelle est la longueur d'onde dans le vide du rayonnement électromagnétique que peut absorber l'espèce chimique pour transiter du niveau E1 vers E2 ? l0 = h c / (E2 - E1) Associer chaque rayonnement à la ( les) transition(s) entre niveaux d'énergie qu'il permet de réaliser : rayonnement transitions UV entre niveaux d'énergie électroniques rayonnement visible entre niveaux d'énergie vibrationnels rayonnement IR UV - visible : transitions entre niveaux d'énergie électroniques ; IR : transitions entre niveaux d'énergie vibrationnels. Principe de la mesure d'absorbance. La grandeur mesurée est soit l'absorbance soit la transmittance de l'échantillon, à une longueur d'onde donnée. Définir ces grandeurs, par une relation faisant intervenir l'inensité lumineuse. On s'appuiera sur un schéma. Lorsqu'une lumière monochromatique d'intensité I0 traverse un milieu homogène, l'intensité de la lumière émergente I décroît exponentiellement lorsque l'épaisseur l du milieu absorbant augmente. I = I0 . e (- al) a est une constante appelée coefficient d'absorption, caractéristique du milieu et de la longueur d'onde considérés. Dans le cas des solutions, la loi de Beer fait intervenir les concentrations. I = I0 . e (- elc) où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance (L mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L). Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L-1. Donner la loi de Beer Lambert en nommant les grandeurs physiques qu'elle fait apparaître. Préciser le domaine de validité et les dimensions de chacune d'elles. La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme : A= log (I0/I) = elc ( A est l'absorbance ou densité optique) e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe. Absorbance et concentration étant proportionnelles, cette relation peut être utilisée pour réaliser des dosages ou des suivis cinétiques. La transmission T est définie comme le rapport de l'intensité transmise à l'intensité incidente. T = I / I0 ; log T= -A. 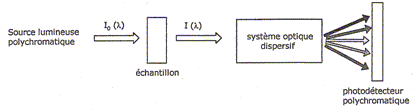Etude de quelques éléments d'un spectrophotomètre UV-visible. 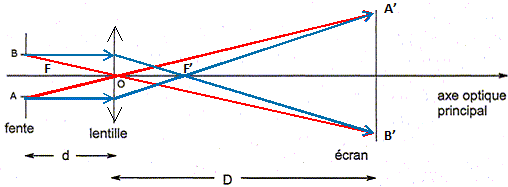Le schéma de principe d'un spectrophotomètre utilisant un photodétecteur à barettes de diodes est le suivant : Etude d'un système optique dispersif. On se propose ici d'étudier le principe de la diffraction et de la dispersion de la lumière par un réseau, élément essentiel d'un spectrophotomètre. Un professeur souhaite montrer à ses élèves le phénomène de la dispersion de la lumière blanche. Que souhaite t-il faire observer à ces élèves ? Le spectre d'une lumière polychromatique obtenu à l'aide d'un verre, milieu dispersif pour la lumière blanche. Parmi les sources lumineuses suivantes, laquelle choisir pour mettre en évidence le phénomène ? Justifier. Lampe à vapeur de sodium, laser à gaz hélium-Néon, lampe quartz-iode. Lampe à vapeur de sodium ( spectre de raies : 2 raies jaunes) ; laser à gaz hélium-Néon ( lumière quasi-monochromatique) lampe quartz-iode ( lumière blanche). Il commence par réaliser l'image d'une fente source AB sur un écran, à l'aide d'une lentille L de centre optique O, de distance focale f' et située à D~ 2 m de l'écran. Quel type de lentille faut-il choisir ? Où faut-il placer la fente par rapport à la lentille pour que l'image soit réelle ? Lentille convergente ; la distance lentille-fente doit être supérieure à la distance lentille- foyer objet. Reproduire le schéma ci-dessous et construire l'image A'B' de AB, indiquer la position des foyers objet F et image F' principaux de la lentille sans souci d'échelle.   Définir le grandissement g de l'image. Donner son expression en fonction de D et d. | g | = A'B' / AB = D / d Où faut-il placer la fente pour que le grandissement soit maximal ? En donner alors une expression approchée en fonction de D et f'. Si d est proche de f' ( tout en restant inférieur) le grandissement, en valeur absolue, est maximum. | g | =D/f'. Dans ces conditions, on souhaite que le grandissement soit, en valeur absolue, égal à 10. Quelle lentille choisir parmi les suivantes ? lentille L1 L2 L3 L4 vergnece ( d) 5 -5 1 -0,2 f' = D/10 = 2,0 /10 = 0,20 m ; vergence V = 1/0,2 = +5 dioptries. Citer deux systèmes optiques que l'on peut placer derrière la lentille pour observer le phénomène de dispersion. Prisme de verre ou réseau.  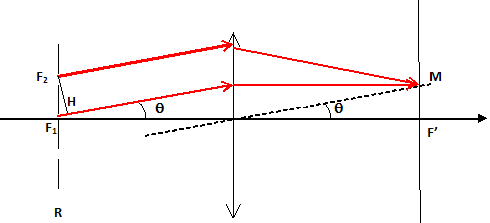Diffraction d'un faisceau parallèle par un réseau. Le réseau R étudié est un réseau plan par transmission, de nombre de traits n par unité de longueur. On considère un faisceau incident monochromatique de longueur d'onde l, frappant le réseau sous incidence normale. Le faisceau est diffracté dans toutes les directions. Il est reçu sur une lentille mince convergente de distance focale f'. Quel est le pas du réseau ?( distance entre deux traits) : a = 1/n On considère que le système optique, centré autour d'un axe horizontal perpendiculaire au réseau, est éclairé dans les conditions de Gauss. Définir ces conditions et en donner les conséquences. Conditions de Gauss : l'objet doit être de petites dimensions et placé au voisinage de l'axe optique principal du système optique. On élimine ainsi les rayons lumineux trop inclinés sur l'axe optique. Un système centré utilisé dans les conditions de Gauss est stigmatique et aplantique. Compléter la figure en indiquant la marche des rayons après traversée de la lentille. Les rayons diffractés dans la direction q convergent après la lentille en un point M. Déterminer sa position yM sur l'axe (F'y) en fonction de f' et q. tan q = yM/f'. Interférences des rayons diffractés. Déterminer la différence de marche d entre les rayons 1 et 2 après la traversée du réseau. Pourquoi cette différence de marche est-elle conservée après le passage des rayons par la lentille ? d = F1H = F1F2 sin q = a sin q avec a = 1/n, pas du réseau. a << f', les deux rayons émergents de la lentille sont quasi confondus et parallèles. Que peut-on dire de la différence de marche entre deux rayons quelconques diffractés dans la direction q ? La différence de marche est un multiple de d = a sin q A quelle condition sur d et l puis sur q, a et l, les rayons diffractés dans la direction q interfèrent-ils de manière constructive en M ? On fera intervenir l'ordre d'interférences k. Ordre d'interférence : différence de marche / longueur d'onde ; k = d / l. L'ordre d'interférence doit être un entier relatif. a sin q / l = k Déterminer les valeurs possibles de k si l = 600 nm et n = 500 traits / mm ( 5 105 traits m-1). a /l = 1/(nl )= 1/(5 105*6 10-7) =10/3 soit sin q =3k/10= 0,3 k. ( avec |sin q |< = 1) k 0 1 2 3 sin q 0 0,3 0,6 0,9 q 0 17,5 36,9 64,2 yM (m) = f' tan q 0 0,31 0,75 2,06 A cela, il faut ajouter les valeurs k= -1 ; k= -2 ; k = -3. Qu'observerait-on sur un écran placé dans le plan focal image de L si n = 500 traits / mm,l = 600 nm et f' = 1,00 m ? On décrira la figure avec précision ( couleurs, distance). Une alternance de tache sombres et brillantes ; la tache centrale est brillante. Les positions des centres des taches brillantes sont données dans le tableau ci-dessus ( yM, dernière ligne) Eclairage en lumière polychromatique. Le réseau est éclairé en lumière polychromatique. On considère les interférences observées à l'ordre 1. Calculer numériquement les angles qv et qr des rayons correspondant respectivement aux radiations violettes ( lv =400 nm) et rouge ( lr =800 nm) interférant de manière constructives à l'ordre 1. rouge violet a /l = 1/(nl) 1/1/(5 105*8 10-7) =2,5 1/1/(5 105*4 10-7) =5 sin q 1/2,5 = 0,4 1/5 = 0,2 q 23,6° 11,5° yM (m) = f' tan q 0,44 0,20 Sur quelle distance le spectre visible d'ordre 1 s'étalera t-il dans le plan focal image de la lentille ? 0,44-0,2 = 0,24 m = 24 cm.

retour -menu