|
Production électrique solaire " dish-stirling" concours physique Capes 2009.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
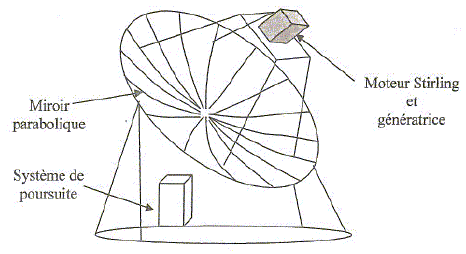
Les vecteurs sont écrits en gras et en bleu. Une unité de production standard "dish-stirling" se compose : - d'un miroir parabolique qui concentre le rayonnement solaire sur un absorbeur que l'on représentera par un disque circulaire placé perpendiculairement à l'axe optique du miroir, - d'un moteur Stirling dont la source chaude est l'absorbeur ; le moteur est refroidi à l'air ou à l'eau, - d'une génératrice entraînée par le moteur, - d'un système de poursuite pour orienter l'axe du miroir vers le soleil en permanence.
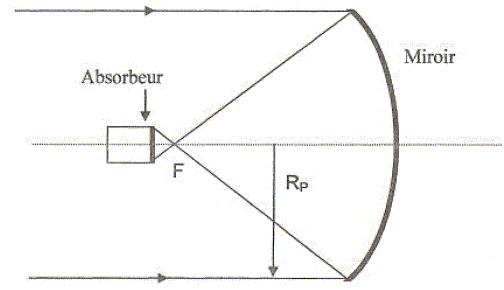
On rappelle la loi de Stefan : j=sT4 avec j la densité surfacique de puissance rayonnée et s = 5,67 10-8 W m-2 K-4 la constante de Stefan. Miroir parabolique et absorbeur.
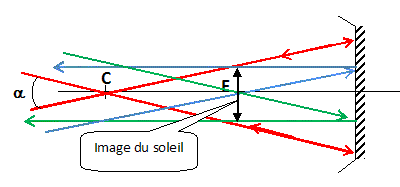
Les rayons incidents parallèles à l'axe de révolution du miroir convergent, après réflexion, en un point appelé foyer du miroir. On modèlise, pour simplifier, le miroir parabolique par un miroir sphérique que l'on suppose utilisé dans le cadre de l'approximation de Gauss. Rappeler les conditions de l'approximation de Gauss et préciser alors la position du foyer. Les rayons incidents doivent être proches de l'axe et peu inclinés sur l'axe principal du système optique. Le foyer de ce miroir sphérique est situé au milieu du segment " centre - sommet du miroir". On assimile le miroir parabolique à un miroir sphérique. Le Soleil étant vu sous un diamètre apparent a=30 minutes d'arc, dessiner l'image du soleil par le miroir. On fera apparaître sur le tracé, la construction de l'image de deux points diamétralement opposés du bord du disque solaire.
Calculer le diamètre d de l'image. 30 minutes d'arc = 0,5° = 0,5*pi/180 = 1,57 / 180 = 8,7 10-3 rad ½d = CF tan (½a) ; a étant petit : ½d ~CF ½ a ; d = CF a = 5* 8,7 10-3 =4,36 10-2 ~4,4 10-2 m. Quelle est la puissance P0 du rayonnement solaire capté par le miroir pour un éclairement E = 800 W m2 ? Aire de la surface collectrice ( miroir de rayon Rp=4,5 m ) : 3,14 *4,52 =63,6 m2. P0 = 800*63,6 =5,1 104 W.
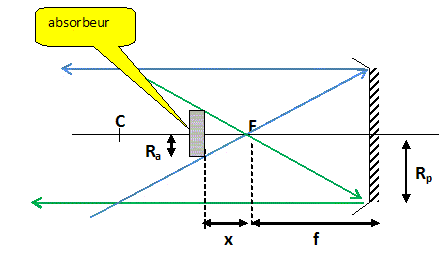
Pour des raisons de tenue thermique, l'éclairement du matériau constituant l'absorbeur est limité par un facteur de concentration en puissance FC= 2500. Calculer le rayon Ra de l'absorbeur en fonction de Rp et FC. Faire l'application numérique. Le facteur de concentration en puissance FC est égal au rapport des surfaces du miroir et de l'absorbeur. FC = pi Rp2/(pi Ra2 ) = Rp2/Ra2 ; Ra= Rp FC-½ = 4,5*2500-½ =9,0 10-2 m. A quelle distance du foyer faut-il placer l'absorbeur pour qu'il soit entièrement éclairé ? Faire l'application numérique.
x / f = Ra/Rp ; x = f Ra/Rp = 5 * 0,09 / 4,5 = 0,10 m. D'une part l'absorbeur réfléchit 18 % du rayonnement qu'il reçoit et d'autre part, il se comporte comme un corps noir du point de vue de l'émission ; c'est à dire qu'il vérifie la loi de Stefan. En dernier lieu, il transmet une puissance Pt au moteur Stirling. La température de fonctionnement du système est Ta= 1040 K. Calculer la puissance Pt transmise au moteur. P0 =5,1 104 W ; tenir compte du rayonnement : 0,82 P0 = 0,82*5,1 104 =4,17 104 W. Loi de Stefan : j=sT4 avec j la densité surfacique de puissance rayonnée et s = 5,67 10-8 W m-2 K-4 la constante de Stefan. Densité surfacique de puissance rayonnée : 5,67 10-8 *10404 =6,63 104 W m-2. Aire de l'absorbeur : 3,14*0,092 =2,54 10-2 m2. Puissance rayonnée : 6,63 104 *2,54 10-2 =1,69 103 W ; Pt =4,18 104 -1,69 103 = 4,0 104 W.
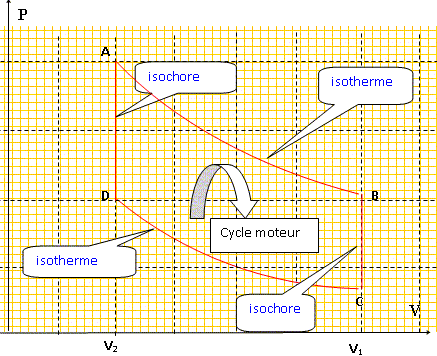
Le moteur de Stirling. C'est un moteur étanche à gaz interne et à source de chaleur externe. Les n miles de gaz interne ( air, hélium ou hydrogène) subissent un cycle de transformations que l'on supposera réversibles : AB : détente isotherme à TC= 900 K. BC : refroidissement isochore à volume V= V1 dans un générateur qui stocke la chaleur échangée CD : compression isotherme à Tf = 300 K. DA : réchauffement isochore à volume V= V2 dans le régénérateur qui lui restitue l'énergie stockée pendant la transformation BC. Le gaz sera assimilé à un gaz parfait. On donne R = 8,314 SI. Ecrire l'équation des gaz parfaits et en déduire l'unité de R. PV = nRT ; R = PV / (nT) ; P : pression soit force / surface ; PV : force / surface * volume ; PV : force * longueur. PV a la dimension d'une énergie d'où R : J mol-1 K-1.
En utilisant le premier principe, calculer le travail W fourni par le gaz au cours d'un cycle en fonction de n, R, TC et Tf et du rapport volumétrique a = V1/V2. On donne a = 2,3 ; n = 0,40 mol. Calculer W et QAB. W = WAB + WCD = -nRTC ln a +nRTf ln a = nR ln a ( Tf -TC) W = 0,40*8,314*ln2,3 (300-600)=-1662 ~ -1,7 103 J. QAB = nRTC ln a =0,40*8,314*900 ln 2,3 =2493 ~2,5 103 J. Définir le rendement théorique rth du moteur et le calculer. Pour quelle raison ce rendement n'est-il jamais atteint ? Rendement : travail utile divisé par l'énergie cédée par la source chaude : rth = -W /QAB = 1662/2493 =0,67. Les transformations réelles ne sont pas réversibles ; elles s'écartent des transformations "idéales", réversibles. Le diagramme de Watt donne W = -790 J et QAB = 2180 J. Calculer le rendement théorique. rréel = 790/2180 =0,36. Le moteur effectue 1080 cycles par minute, en déduire la puissance du moteur. 1080/60 = 18 cycles par seconde d'où la puissance : 790*18 = 14,2 kW. Quelle est la puissance fournie par l'absorbeur au moteur ? 2180*18 = 39,2 kW, valeur à peu près égale à la puissance transmise par l'absorbeur ( calcul ci-dessus).
|
|||||||
|
|
|||||||
|
|
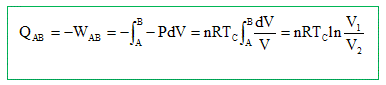 positif, reçu par le fluide de la source
chaude
positif, reçu par le fluide de la source
chaude