|
Dipôles RLC, RL, RC : physique concours ECE 08
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||
| .
. |
||||||
|
||||||
|
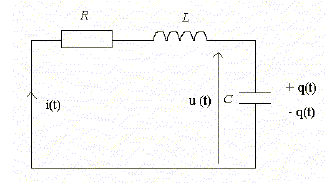
Répondre par vrai ou faux. On considère le circuit de la figure ci-dessous, R est la résistance d’un conducteur ohmique, L est l’inductance d’une bobine dont la résistance est négligeable, C est la capacité d’un condensateur. On étudie la décharge du condensateur dans la bobine et les oscillations qui en résultent.
On désigne par q(t) la charge instantanée du condensateur à la date t. i(t) est l’intensité instantanée dans le circuit et u(t) est la tension instantanée aux bornes du condensateur, à la date t. A- L’expression de i(t) en fonction de u(t) s’écrit i(t) = du(t)/ft. Faux. i(t) = dq/dt avec q = C u(t) ; dq/dt= C du(t) / dt d'où i(t) = C du(t)/dt. B- L’équation différentielle à laquelle satisfait u(t) est Ldi/dt -u(t) = LC d2u/dt2 -u(t) =0. Faux. Additivité des tensions : u(t) + Ldi/dt + R i = 0. i(t) = C du(t)/dt ; di/dt = C d2u/dt2 u(t) + LC d2u/dt2 + RC du(t)/dt = 0. On suppose d’abord que la résistance R est nulle. La tension initiale est u(0) = E. C- L’expression de u(t) =E cos (2 pi t / T0) est solution de l’équation différentielle dans ce circuit avec T0 = 2 pi (LC)½. Vrai. u(t) + LC d2u/dt2 =0 (1); u' =-2 pi E/ T0 sin (2 pi t / T0) ; u" = -4 pi2 E/ T02 cos (2 pi t / T0) = -4 pi2/ T02 u(t). repport dans (1) : u(t) -LC 4 pi2/ T02 u(t) = 0 est vérifiée quel que soit t si LC 4 pi2/ T02 = 1. D- L’expression de i(t) est Cdu(t)/dt = -CE 2 pi / T0 sin (2 pi t / T0). Vrai.
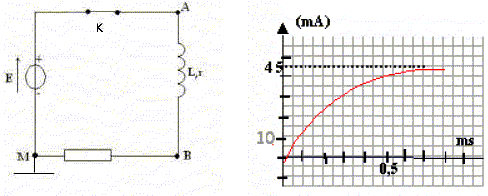
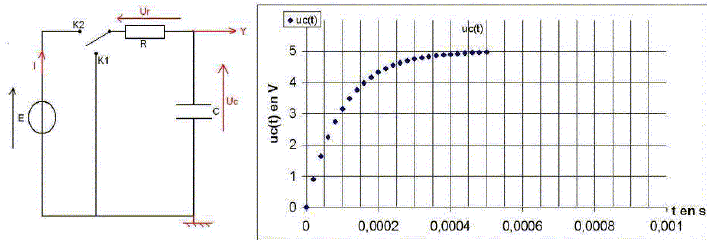
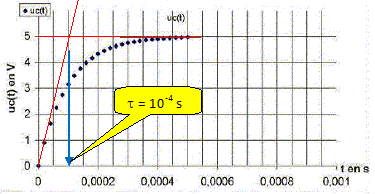
La f.e.m de l'alimentation stabilisée utilisée est E=9 V . L'interface reliée à l'ordinateur permet d'étudier les variations de uR (t). La constante de temps t du circuit déduite de la courbe est proche de 0,25 ms.
lecture graphe : l'asymptote horizontale a pour équation I0 = 45 mA. B- La valeur de la résistance interne r de la bobine est r = 10 kiloohms. Faux. En régime permanent l'intensité I0 est constante. la tension aux bornes de la bobine vaut : rI0. Additivité des tensions : E = RI0+rI0 ; r = E/I0 -R = 9/0,045 -190 = 200-190 = 10 ohms. C- La valeur de l’inductance est L=10 H. Faux. La constante de temps t du circuit vaut : t = L/(R+r) = 0,25 ms = 2,5 10-4 s. L = t (R+r)=2,5 10-4 *200 = 0,05 H. On ajoute au circuit une seconde bobine identique à la précédente. Les deux bobines sont placées en série. D- La constante de temps a changé et est environ le double de t . Vrai. t = 2L/(R+2r) = 0,1 /(190+20) =0,1 / 210 ~4,8 10-4 s~ 0,48 ms.
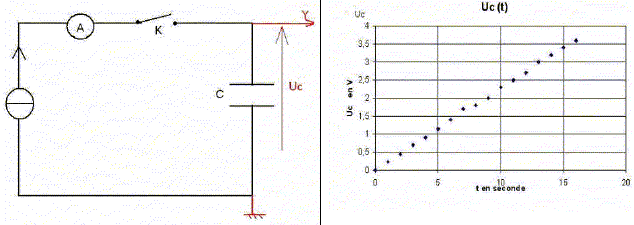
Un condensateur de capacité C=100 microfarads est préalablement chargé sous la tension U=1000 V. On installe ce condensateur dans un circuit comportant une résistance R=100 kiloohms et un interrupteur. On ferme l'interrupteur à l'instant t=10 s. A- A l'instant de la fermeture, la différence de potentiel entre les armatures du condensateur vaut 1000 V, et le courant dans le circuit a une intensité de 10-3 A. Faux. Continuité de la tension aux bornes du condensateur u (t=10) = 1000 V ; discontinuité de l'intensité : i(t=10) = 1000 / 105 = 10-2 A. B- A l'instant de la fermeture, la différence de potentiel entre les armatures du condensateur montre une tendance à la diminution, avec une perte de tension initiale de 10 V s-1. Faux. Coefficient directeur de la tangente à t= 10 s à la courbe uc=f(t) : -U / (RC) =-1000/ 105*10-4) =-100 V/s. C- A l'instant t=20 s, la différence de potentiel aux bornes du condensateur n'est plus que de 370 V environ. Vrai. A la date t =t0+ t , la tension aux bornes du condensateur vaut environ : 0,37 U ~ 370 V. D- A l'instant t=60 s, le condensateur est virtuellement entièrement déchargé, et le courant dans le circuit négligeable. Vrai. A la date t =t0+ 5t , le condensateur est pratiquement déchargé et l'intensité du courant est voisine de zéro.
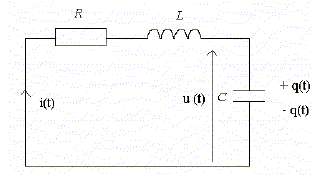
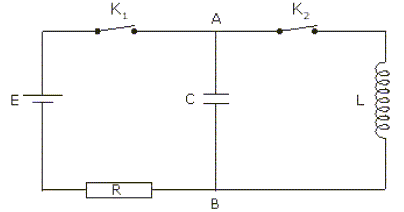
On considère le montage électrique représenté ci-dessous :
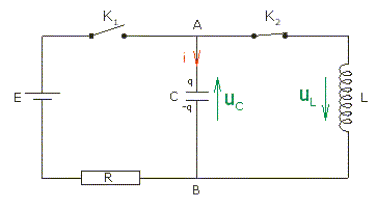
Le circuit comprend un générateur de tension idéal E=10 V, deux interrupteurs K1 et K2, une bobine inductive L=10 mH (de résistance interne nulle), un conducteur ohmique R=1 kiloohm et un condensateur de capacité C=10 nF. A l'instant t la charge de l’armature A du condensateur est q et la tension à ses bornes est Uc. L’intensité du courant dans le circuit est i. Le condensateur étant déchargé, on laisse l'interrupteur K2 ouvert et on ferme K1. A- la charge q de l'armature A est négative. Faux. A est relié à la borne positive du générateur. On se place à la fin de la charge ; q est alors constante. B- la valeur de l'intensité du courant à travers le conducteur ohmique est nulle. Vrai. C- La tension aux bornes du condensateur est Uc= 10 V. Vrai. D- La charge du condensateur est q0 = 0,1 microcoulomb. Vrai. q0 = C Uc =10-8 *10 = 10-7 C. Le condensateur étant chargé, on ouvre l'interrupteur K1 et on ferme K2 à l'instant t0=0 ; pi ~ 3.
A- La tension aux bornes du condensateur obéit à l’équation différentielle suivante : LCu"c -uc=0 Faux. additivité des tensions : uc+uL=0 ; uc+Ldi/dt=0 avec i = dq/dt = Cduc/dt et di/dt = Cd2uc/dt2= Cu"c. uc+Ldi/dt=0 donne : LCu"c +uc=0 B- La solution de cette équation différentielle est : uc(t) = 10 cos(105t + pi). Faux. LC =10-2*10-8 =10-10 ; (LC)½ = 10-5 ; pulsation w =1/(LC)½) = 1/10-5 ; uc(t=0) = 10 cos(pi) = -10. or la continuité de la tension impose uc(t=0) = + 10 V ; uc(t) = 10 cos(105t) C- La période des oscillations qui prennent naissance dans le circuit est d’environ T0 = 6 10-5 s. Vrai. T0 = 2 pi (LC)½ =2*3 *10-5 = 6 10-5 s. D- L'énergie électromagnétique E du circuit étudié est 0,5 10-7 J. Faux. Conservation de l'énergie : ½ CUc2 = ½Li2 = 0,5*10-8 *102 =0,5 10-6 J.
|
||||||
|
|
||||||
|
|