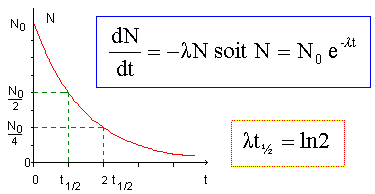|
Datations : carbone 14 et
thermoluminescence
concours
général 2009.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
La loi de décroissance radioactive d’une population d’atomes de 14C s’écrit : N(t) =N0exp(-lt), où N0 est le nombre de noyaux initialement présents dans l’échantillon, l la constante radioactive et t le temps. Ecrire la réaction de désintégration du 14C sachant que la particule créée dans ce cas est un électron : 0-1e 146C ---> 147N* +0-1e + antineutrino suivie de la désexcitation du noyau fils 147N* ---> 147N + 00g. Rappeler la signification du terme « temps de demi-vie » noté t½. La demi-vie radioactive,(ou période) notée t½, d'un échantillon de noyaux radioactifs est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés. Tracer la courbe N=f(t).
Retrouver la relation qui lie le temps de demi vie t½ à la constante radioactive l. N(t½) = N0exp(-lt½) = 0,5 N0 ; exp(-lt½) = 0,5 ln (0,5 ) = - ln 2 = -lt½ ; lt½ = ln 2. En déduire la valeur de l en unité du système international. ln 2 est sans dimension ; l est donc l'inverse d'un temps ; l s'exprime en s-1. Expliquer, grâce à votre courbe, comment il est alors possible de déterminer l’âge d’un échantillon. N(t) est déterminé expérimentalement ; à partir de cette valeur, tracer une droite horizontale ; à partir de l'intersection avec la courbe tracer une droite verticale. Cette droite coupe l'axe des temps ( abscisse) à la date cherchée. Cette méthode
repose sur le calcul de la proportion
14C/12C. On doit alorss
considérer que la
désintégration se fait de
manière uniforme et
régulière. La proprotion
14C/12C doit ête
supposée constante depuis des
millénaires. On estime possible de
dater des échantillons jusqu’à
50000 ans.
Pourquoi n’est-il
pas possible d’aller au delà
? La demi-vie du carbone 14
est de l'ordre de 5700 ans ; 50 000 ans correspond
à environ 9 t½. Il reste alors dans
l'échantillon : N(t) = N0 /
29 ~ 2 10-3
N0. La proportion de 14C à mesurer
est si faible qu’aucun détecteur ne
s’est avéré suffisamment
sensible. Il est théoriquement possible de dater tout objet constitué de matériaux organiques, tels que des ossements, des objets en bois, mais aussi des argiles et des poteries ou encore des céramiques, objets a priori minéraux, mais dont la composition recèle souvent des traces de matériaux organiques (souvent désagrégés). Cependant dans le domaine des poteries et céramiques, une seconde méthode est privilégiée, celle de la thermoluminescence. Principe de la technique. Le phénomène de thermoluminescence fut observé pour la première fois en 1663 par Sir Boyle, qui vit une lueur en réchauffant un diamant dans l’obscurité. En 1930 les physiciens du solide Urbach et Frisch en expliquèrent le principe grâce à leurs études sur les pièges à électrons dans les cristaux. La méthode de datation ou d’identification par thermoluminescence ne fut finalement utilisée qu’à partir de 1950 lorsque la technologie des photomultiplicateurs permit de détecter de très faibles quantités de lumière. La thermoluminescence est un phénomène physique qui se traduit par la propriété qu’ont certains cristaux d’émettre de la lumière lorsqu’on les chauffe, à condition qu’ils aient été au préalable soumis à une irradiation naturelle ou artificielle. Cette luminescence ne se produit que si le chauffage a été précédé d’une irradiation due à des rayonnements ionisants, par exemple l’exposition à la radioactivité naturelle pendant des milliers d’années. Les rayonnements ionisent les atomes sur leur passage. Ils créent ainsi des charges temporairement libres, des électrons. Un cristal n’est jamais parfait, il contient de très grandes quantités d’impuretés ou de défauts ponctuels dont certains peuvent constituer des sites « pièges » pour les électrons libérés par l’irradiation. Continuellement au cours du temps, au passage d’une particule radioactive, des électrons libérés par l’irradiation sont ainsi piégés dans des états physiques dits métastables. L’irradiation étant supposée constante, le nombre de charges capturées est donc proportionnel au temps pendant lequel les cristaux sont irradiés tant que les pièges ne sont pas tous occupés. Si on chauffe un cristal ayant été irradié, l’apport d’énergie thermique, selon la température atteinte, peut « vider » les pièges. Les électrons alors libérés dans le cristal se recombinent avec un ion positif créé lors de l’irradiation. L’énergie dégagée lors de ces recombinaisons est libérée par le cristal sous forme de photons d’où la production de lumière.
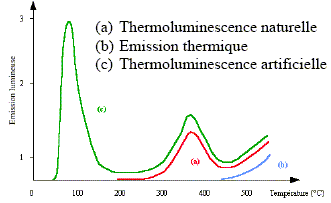
Pour un type de chauffage donné, le nombre de photons émis est proportionnel au nombre d’électrons libérés par le chauffage, lui même proportionnel au nombre de charges initialement créées lors de l’ionisation, lui même proportionnel au temps écoulé depuis le dernier vidage des sites pièges (instant initial). Cet instant initial correspond à l’effacement des irradiations antérieures. En datation par thermoluminescence, on recherche le coefficient de proportionnalité entre la quantité de lumière émise au cours du chauffage au laboratoire et la dose d’irradiation Q reçue par le cristal depuis l’instant initial. Pour obtenir un âge, il faut aussi connaître la dose d d’irradiation reçue par le cristal en une année. Le temps écoulé depuis l’instant initial est : Age = Q / d. (L’unité de dose d’irradiation est le gray. Q est donc exprimé en gray et d en gray / an.)
|
|||||||
|
c |
|||||||
|
|