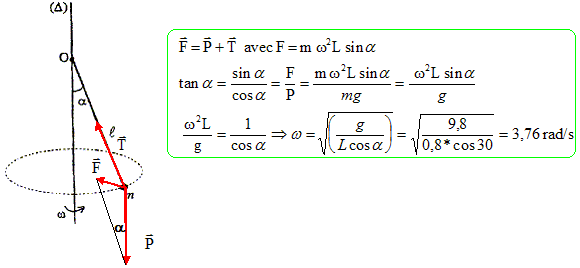QCM chute, projectile, radioactivité, dipole RC ( 11 questions) : concours kiné Poitiers 1999. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

On imagine qu'on lâche sans vitesse initiale et en même temps, à la surface de la Lune deux objets O1 et O2 de masse respective m1 = 100 g et m2 = 100 g. Les deux objets sont initialement sur la même ligne horizontale, à la hauteur h = 2 m au dessus du sol lunaire. On donne l'accélération de la pesanteur à la surface de la Lune : gL = 1,6 m s-2. Quelle proposition est vraie ? - les deux objets sont dans un état d'apesanteur ( ils sont soumis à la force de gravitation exercée par la Lune) - l'objet O2 arrive le premier sur le sol lunaire ( la durée de la chute libre est indépendante de la masse) - la vitesse de O1 juste avant de toucher le sol est la moitié de celle de O2, au même instant (la vitesse ne dépend pas de la masse ) - la vitesse de O1 juste avant de toucher le sol est 2,5 m/s ( v = (2gLh)½ = (2*1,6*2)½ =2,5 m/s ) Vrai. - le temps mis par O2 pour toucher le sol est 16 s. ( h =½gLt2 ; t2 =2h/gL=4/1,6 =2,5 s2). On donne g = 10 m s-2 et la célérité du son dans l'air v = 340 m/s. Pour déterminer la profondeur approximative d'un puits, on lâche sans vitesse initiale, du bord du puits, une pierre et on déclenche simultanément un chronomètre. Lorsqu'on entend l'impact de la pierre dans l'eau du puits on arrête le chronomètre : le temps indiqué est de trois secondes. La profondeur approximative du puits est : 10 m ; 20 m ; 30 m ; 40 m ; 50 m On néglige les frottements sur les couches d'air : la chute de la pierre est libre ; on note t la durée de la chute de la pierre. h = ½gt2 = 0,5*10*t2 = 5 t2. On note t' la durée mise par le son pour remonter : t' =h / v ; h = vt' = 340 t'. Par suite : 5 t2 =340 t' avec t + t' = 3 ; t' = 3-t 5 t2 =340(3-t) ; 5 t2 +340 t -1020 = 0 D = 3402+4*5*1020 = 136000 ; D½ =368,78 ; t = (-340 +368,78) / 10 = 2,878 s par suite h = 5 t2 = 5*2,8782 =41,4 m. Par désintégration radioactive, les noyaux d'uranium 23892U se transforment en noyau de plomb 20682Pb en émettant simultanément des particules a et ß-. choisir parmi les propositions suivantes le nombre de désintégration alpha d'une part et ß- d'autre part, qui permettent, ensemble, de passer de l'uranium au plomb. - 32 désintégrations alpha et 10 désintégrations ß- ; Vrai - 10 désintégrations alpha et 32 désintégrations ß- ; - 8 désintégrations alpha et aucune désintégration ß- ; - 6 désintégrations alpha et 8 désintégrations ß- ; - 8 désintégrations alpha et 6 désintégrations ß-. Lors d'une désintégration ß- le nombre de masse A ne change pas. Lors d'une désintégration alpha, le nombre de masse diminue de 4 : par suite (238-206) / 4 = 8. Lors d'une désintégration alpha, le nombre de charge diminue de 2 et lors d'une désintégration ß- , le nombre de charge augmente de 1 : par suite 82-92 = -10 ; -10 = - 2*8 +6. Le radium 22688Ra se désintègre en radon 222Rn par émission a. On donne : c = 3 108 m/s ; m(Ra) = 226,0254 u ; m(Rn) = 222,0175 u ; m(a) = 4,0015 u. 1 u = 1,67 10-27 kg ; 1 MeV = 1,6 10-13 J. L'énergie libérée par la réaction de désintégration d'un noyau de radium est : 200 MeV ; 9,6 10-18 J ; 6 MeV. Perte de masse Dm = m(a) + m(Rn) - m(Ra) =4,0015 +222,0175-226,0254 =-0,0064 u -0,064*1,67 10-27 = -1,069 10-29 kg. Energie libérée : E = Dm c2 = -1,069 10-29 *(3 108)2 =-9,62 10-13 J. -9,62 10-13/ 1,6 10-13 = -6,0 MeV. En supposant que toute l'énergie libérée par la réaction soit transformée en énergie cinétique de la particule a, la vitesse acquise par ces particules est environ : 35 000 km/s ; 17000 km/s. Dans l'hypothèse d'une particule non relativiste E = ½m(a) v2. m(a) = 4,0015*1,67 10-27 =6,68 10-27 kg v2 = 2E / m(a) = 2*9,62 10-13/ 6,68 10-27 =2,88 1014 ; Prendre la racine carrée v = 1,7 107 m/s = 1,7 104 km/s. 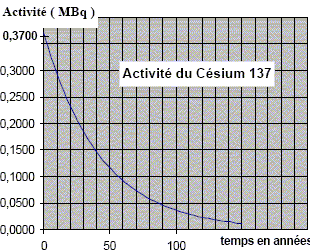Le document ci-dessus représente la loi de décroissance radioactive du césium 137. L'activité initiale de cette source, au moment de sa fabrication est A0=0,3700 MBq. Le césium 137 est un émetteur ß-. Chaque désintégration s'accompagne d'un photon g d'énergie 0,622 MeV. La période radioactive du césium 137 est : 30 ans ; 70 ans. Au bout d'une période ( demi-vie) l'activité est égale à la moitié de l'activité initiale. La lecture du graphe conduit à t½ ~ 30 ans.  En manipulant près de la source pendant une heure, un étudiant absorbe une petite fraction du rayonnement g émis par la source. On suppose que la fraction d'énergie absorbée par l'étudiant est 10 %. D'autre part, il s'est écoulé 8 ans depuis la fabrication de la source. Dans ces conditions l'étudiant absorbe une énergie d'environ : 1,1 105 J ; 1,1 10-5 J ; 0,1 MBq. L'activité A au bout de 8 ans est voisine de 0,300 MBq ( lecture graphe) soit 3 105 désintégrations par seconde ; 3 105 *3600 =1,08 109 désintégrations en une heure. L'étudiant absorbe 10 % des photons soit : 1,08 108 photons.  Energie absorbée : 1,08 108 *0,622 =6,7 107 MeV 6,7 107 *1,6 10-13 = 1,1 10-5 J.     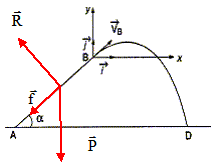On étudie le mouvement d'un skieur nautique lors d'un saut au tremplin. Les frottements de l'air sont négligés. Le skieur de masse m =65 kg aborde un tremplin de longueur AB = 8 m faisant un angle a=40° avec l'horizontale. Le skieur quitte le tremplin en B avec une vitesse tangente au tremplin de valeur vB = 51,2 km/h. Les frottements le long du tremplin sont équivalents à une force constante f, parallèle au tremplin, opposée au mouvement, de valeur f =550 N. On donne g = 9,80 m/s2. La vitesse VA du skieur lorsqu'il aborde le tremplin vaut : 3,1 km/h ; 22,9 m/s ; 32,9 m/s ; 82,5 km/h ; 102 km/h. Travail résistant du poids en montée : -mgABsina =-65*9,8*8*sin40 = -3797 J Travail résistant des frottement : -f AB = -550*8 = -4400 J L'action du plan, perpendiculaire à la vitesse ne travaille pas. Appliquer le théorème de l'énergie cinétique entre A et B : ½m vB2 - ½mvA2 = somme des travaux des forces = -4400 -3797 =-8197 J vB = 61,2 / 3,6 = 17 m/s. vA2 = vB2 +2*8197 / m ; vA2 = 172 +2*8197 / 65 = 541,2 prendre la racine carrée : vB = 23,3 m/s = 23,3*3,6 km/h =83,7 km/h. Un solide glisse sans frottement sur un plan incliné selon la plus grande pente du plan. Dans un repère convenablement choisi, on relève la position x du centre d'inertie du solide en fonction du temps. Choisir parmi les graphes ci-dessous, celui qui vous semble représenter la position du solide en fonction du temps. Repère : origine en haut du plan, axe parallèle au plan dirigé vers le bas du plan. Le mouvement étant accéléré, on ne retient pas les graphes A, B et C. Graphe D : la tangente initiale est horizontale : la vitesse initiale est donc nulle. Graphe E : la tangente initiale est verticale : la vitesse initiale serait donc très grande. Le graphe D est le plus probable. Un pendule conique est constitué d'une masse ponctuelle m suqpendue à un fil sans masse de longueur L. Ce pendule est en mouvement de rotation uniforme autour d'un axe vertical D. l =0,8 m ; m = 100 g ; g = 9,8 m s-2 . Lorsque le fil est incliné d'un angle a = 30 ° par rapport à la verticale, la vitesse angulaire est : 3,50 rad/s ; 3,76 rad/s ; 1,19 rad/s ; 2,50 rad/s ; 1,35 rad/s.     On étudie un circuit comprenant une résistance , une inductance et un condensateur, en série, soumis à une tension sinusoïdale. Si la valeur de la capacité C du condensateur est multipliée par 4, la fréquence de résonance du circuit est : multipliée par 2 ; divisée par 2 ; multipliée par 4 ; divisée par 4 ; inchangée. A la résonance LCw2 = 1. Si L est constant et si C est multiplié par 4 alors w2 est divisé par 4. w est donc divisée par 2. Or la pulsation et la fréquence sont proportionnelles ( w = 2 pi f ): la fréquence est divisée par 2. On branche entre N et P un générateur qui impose une tension constante U = VP-VN = 12 V. Après un régime transitoire, la tension UC aux bornes du condensateur initialement déchargé reste constante. Cette tension UC vaut alors : 0 ; 4 V ; 6 V ; 8 V ; 12 V. 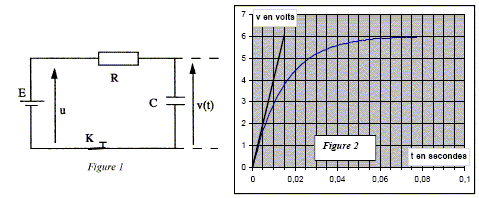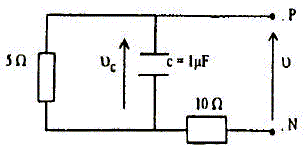Le schéma ci-dessous correspond au condensateur chargé :   E représente un générateur de courant continu idéal de fem 6 V. R est un conducteur ohmique, C un condensateur de capacité C et K un interrupteur. K étant fermé on réalise l'enregistrement de la tension v(t) aux bornes du condensateur initialement déchargé. Sur la figure on a représenté la tangente à l'origine. Trouver la valeur de R et de C parmi les choix ci-dessous. R = 1000 W ; R = 2000 W ; R = 4000 W ; C =2,52µF ; C =3,75 µF. L'intersection de la tangente à l'origine avec l'asymptote horizontale (v = 6 V) donne la constante de temps du circuit : RC =0,015 s. Si R = 1000 W alors C = 0,015/1000 = 15 µF Si R = 2000 W alors C = 0,015/2000 = 7,5 µF Si R = 4000 W alors C = 0,015/4000 = 3,75 µF.

retour -menu