Mécanique : le looping, concours ITPE 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

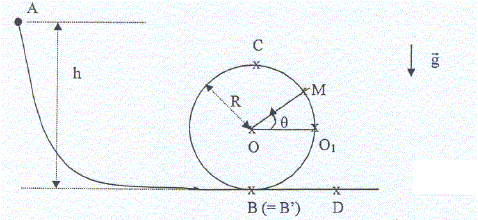
On considère un point matériel M de masse m pouvant se déplacer sans frottements sur le profil décrit sur la figure ci-dessous. Ce profil est un « support », le point M représente par exemple un petit véhicule de manège se déplaçant sur des rails et effectuant un « looping ». La hauteur h est supérieure au diamètre 2R. Le point M est lâché sans vitesse initiale du point A. En B, il suit le profil circulaire décrit par la boucle de centre O et rayon R, en tournant dans le sens trigonométrique. Cette boucle est en fait une hélice très aplatie (en toute rigueur M passe en B' après la boucle; on admettra que B'= B). On considérera que le mouvement est circulaire sur la boucle BCB (et non hélicoïdal). Eventuellement de retour en B, le point continue sa course vers D, puis au delà. Donnée s: m = 10 kg ; h = 20 m ; R = 5 m ;g = 10m s-2 (accélération de la pesanteur) Calculer la vitesse VB du point M en B. Comparer VBet VD. Entre A et B, en l'absence de frottements, l'énergie mécanique se conserve. L'énergie mécanique en A est sous forme potentielle de pesanteur : EM(A) = mgh L'énergie mécanique en B est sous forme cinétique : EM(A) = ½mV2B. La conservation de l'énergie mécanique conduit à : V2B = 2 gh ; VB = (2 gh )½ =(20*20 )½ = 20 m/s. Entre B et D, en l'absence de frottement, l'énergie mécanique se conserve : B et D étant à la même altitude, les énergies cinétiques en B et en D sont identiques. Donc VB= VD. Exprimer la vitesse V du point M en un point de la boucle BCB. altitude du point M ( par rapport à B, origine des altitudes) hM= R + R sin q = R(1+sin q ) Energie mécanique du solide en M : EM(M) = mgR(1+sin q ) + ½mV2. Conservation de l'énergie mécanique : EM(M) = EM(A) mgR(1+sin q ) + ½mV2 = mgh V = (2g (h-R(1+sin q ) ) )½. Définir, exprimer et dessiner la réaction R exercée par le support sur le point matériel M. 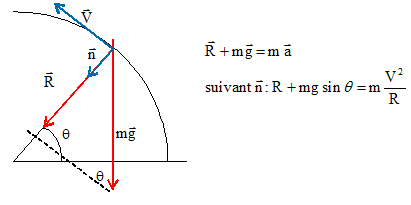Réaction = m (V2/R - g sin q ) et V2 = 2gh -2g R(1+sin q ) ; Réaction = m ( 2gh/R -2g-3gsin q ) Réaction = 10(20*20/5 -20 -30 sin q ) ; Réaction = 600-300 sin q. sin q, fonction croissante entre -90° et +90 ° : donc Réaction décroît de 900 N à 300 N. sin q, fonction décroissante entre +90° et +270 ° : donc Réaction croît de 300 N à 900 N. Réaction est minimale au sommet de la trajectoire et vaut 300 N ; avec h = 20 m, Réaction ne s'annule pas. 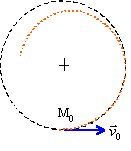A quelle condition le point M quitte-t-i1 le profil ? En déduire une condition sur la hauteur h. Quel est alors son mouvement ultérieur ? Réaction = m ( 2gh/R -2g-3gsin q ) Si Réaction s'annule, le solide quitte la piste circulaire : 2gh/R -2g-3gsin q = 0 Au point le plus haut ( sin q = 1), on ne quitte pas le profil si Réaction est supérieure ou égale à zéro. 2gh/R -2g-3g =0 ; 2h/R = 5 ; h = 2,5 R = 2,5*5 = 12,5 m. La valeur minimale de la hauteur h est 12,5 m, afin que le solide ne quitte pas la piste circulaire. Si h est inférieure à 12,5 m, le solide quitte la piste avant d'atteindre le point le plus haut : son mouvement est alors une chute libre. (courbe orange ) Si le solide n'atteint pas le point O1, il ne quitte pas le profil, mais rebrousse chemin. Il en résulte un mouvement oscillatoire autour de B. Hauteur minimale permettant d'atteindre O1avec une viteese nulle : mgh = mgR soit h=R = 5 m. Si h est compris entre 5 m et 12,5 m, le solide quitte le profil et son mouvement ultérieur est une chute libre. Calculer hlim,la hauteur limite (on précisera si elle est minimale ou maximale) afin que le point puisse atteindre le point D. Pour atteindre le point D, il suffit de passer en C ( après ça descend ) avec une réaction du support supérieure ou égale à zéro. La hauteur cherchée est supérieure ou égale à 12,5 m ( voir calcul ci-dessus ). Quelle est alors le mouvement de M sur la partie BD ? Le point s' arrêtera-t-il par la suite ? Sur la partie BD, la vitesse reste constante : le mouvement est rectiligne uniforme. D'après le principe d'inertie, le solide est soumis à des forces qui se neutralisent. En l'absence de frottement, le solide se déplace à vitesse constante et ne s'arrête pas. Mais dans la réalité, il existe des frottements et le solide va finir par s'arrêter.

retour -menu