Au volley-ball : projectile ( concours manipulateur radio Tours 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

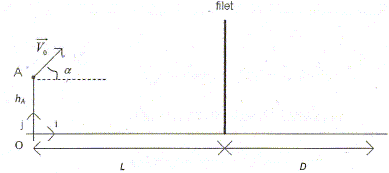
Au volley-ball, Ie joueur qui effectue Ie service frappe Ie ballon à la hauteur hA du sol et à la distance L = 11,0 m du filet. Le fond du court est à une distance D = 9,0 m du filet. La hauteur du filet est H = 2,4 m. Pour que Ie service soit bon, il faut que le ballon passe au-dessus du filet et touche Ie sol dans Ie camp adverse. Lors d'un service, à I'instant de date t = 0, un joueur amateur frappe Ie ballon en A, situé à une hauteur hA = 1,0 m. La vitesse initiale V0 a une valeur V0 = 14 m /s et fait un angle a = 45° avec I'horizontale. On négligera toutes actions de I'air. On prendra g = 10 m.s-2. Les données et les calculs à effectuer concernent Ie centre d'inertie du ballon. On travaillera en utilisant Ie repère du schéma). Aide aux calculs: 14 x sin 45 = 14 x cos 45~10 ; 11 *11 ~ 120. Etablir les expressions des coordonnées de la vitesse : Vx(t) et Vy(t) en fonction des données. En déduire les expressions numériques de Vx(t) et Vy(t). Le ballon n'est soumis qu'à son poids ; la seconde loi de Newton conduit à l'accélération : Un vecteur est écrit en gras et en bleu. a ( 0 ; -g) ; a ( 0 ; -10) ; Le vecteur vitesse est une primitive de l'accélération : v ( V0 cos a ; -gt +V0 sin a) ; Vx(t) = V0 cos a = 14 cos 45 = 10 m/s. Vy(t) = -gt +V0 sin a =-10 t + 14 sin 45 = -10 t +10. Etablir les équations horaires x(t) et y(t) en fonction des données. En déduire les expressions numériques de x(t) et y(t). Le vecteur position est une primitive du vecteur vitesse. x(t) = V0 cos a t = 10 t. (1) y(t) = -½gt2 +V0 sin a t +hA = - 5 t2 + 10 t + 1,0. (2) Etablir, littéralement, I'équation cartésienne de la trajectoire. En deduire I'expression numérique de y(x). (1) donne t = x / (V0 cos a) ; repport dans (2) : y = -½g x2 / (V0 cos a)2 +x tan a + hA. y = -5x2/100 + x +1,0 ; y = -0,05x2 + x + 1,0. (3) Le ballon passe-t-i1 au-dessus du filet ? Justifier. Le filet se trouve à l'abscisse x = 11 m. Remplacer x par 11 dans (3) : y(11) = -0,05*112 +11 + 1,0 = -0,05*120 +12 = -6+12 = 6 m. y(11) est supérieur à la hauteur h du filet ; le ballon passe au dessus du filet. Donner I'équation qui permet de calculer l'instant pour lequelle ballon touche Ie sol, si ce dernier n'est pas intercepté. Au sol y(t) est nulle : -½gt2 +V0 sin a t +hA = - 5 t2 + 10 t + 1,0 = 0. La résolution de cette équation donne t = 2,1 s. A quelle distance de O se trouve-t-il alors ? Dans x(t) = V0 cos a t = 10 t, remplacer t par 2,1 : x(2,1) = 21 m. Cette valeur est supérieure à L+D = 20 m. le service est mauvais. Le ballon passe au-dessus du filet mais ne touche pas le sol dans Ie camp adverse.

retour -menu