Gravimètre supraconducteur, gravimètre absolu à chute : concours général 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

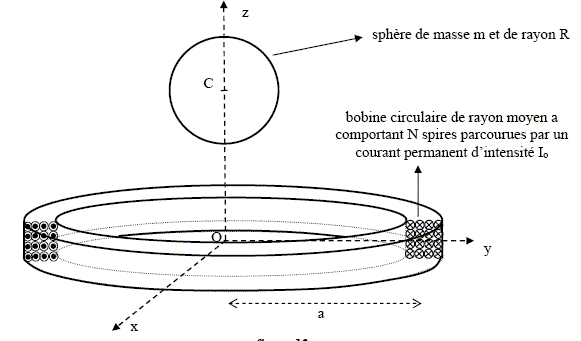
Le principe d’un gravimètre supraconducteur est de réaliser l’équilibre d’une sphère en niobium soumise d’une part à l’action de son poids et d’autre part à l’action d’une force de « lévitation magnétique ». La force de « lévitation magnétique » résulte de l’action du champ magnétique, créé par deux bobines parcourues par un courant permanent, sur les courants qui parcourent la sphère. La sphère en niobium ainsi que les bobines sont à l’état supraconducteur, c’est-à-dire notamment que leur résistance électrique est nulle. Ceci exige, en particulier, d’opérer dans un bain d’hélium liquide dont la température est de 4,2 K, condition indispensable pour pouvoir observer le phénomène de « lévitation magnétique ». Le but de cette partie est d’illustrer de manière simple le principe de la mesure de la variation de g. On s’appuie sur la figure suivante qui représente la sphère supraconductrice de masse m, de rayon R et de centre C qui se déplace le long de l’axe vertical ascendant Oz et l’une des bobines qui crée le champ magnétique responsable de la lévitation de la sphère. 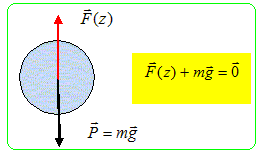Le référentiel d’étude ( O,x,y,z ) situé à la surface de la Terre sera considéré comme galiléen. Les vecteurs sont écrits en gras et en rouge. On suppose que la force de lévitation d’origine magnétique subie par la sphère s’écrit : F = F(z) ez où ez est un vecteur unitaire de l’axe des z orienté vers le haut et F(z) = a z/ (a2+z2)4 I20, avec a =1,25.10-12 N.m7.A-2 ; le paramètre a désigne le rayon moyen de la bobine circulaire et I0 l’intensité du courant qui circule dans les spires. On note g l’intensité du champ de pesanteur. On limite l’étude à la demi-droite z positive ou nul. Existence d’un équilibre. Justifier la dimension de la constante a. a= F(z) (a2+z2)4 / (zI20) force = masse * accélération = masse * longueur / temps2 ; [F'z)] = M L T-2. [(a2+z2)4 / z] = L7 ; [1/I20] = A-2 d'où : [a] = M L T-2 L7 A-2 = M T-2 L8 A-2 ou N L7 A-2. Représenter sur un schéma les deux forces qui s’exercent sur la sphère et écrire la condition de l’équilibre de celle-ci. 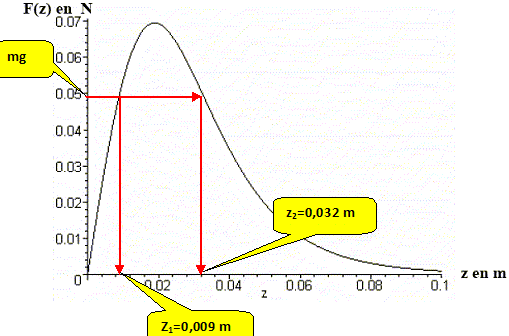On admet que le maximum de la fonction F(z) est obtenu pour z = 7-½ a. En déduire l’expression littérale de la valeur minimale Imin du courant I0 pour que la lévitation magnétique soit possible. Fmax doit être supérieure au poids ; Fmax =a 7-½ a / (a2+a2/7)4 I20 = a I20 / (4,5 a7 ) a I2min / (4,5a7 )> mg ; a I2min > mg(4,5 a7 ) ; I2min > mg(4,5 a7 ) /a . A.N : a = 5,0 cm ; m = 5,0 10-3 kg ; g=9,8 m s-2. I2min > 5,0 10-3 *9,8 *4,5 (5,0 10-2)7 /(1,25.10-12) ; I2min >137,6 ; Imin >11,7 A. Stabilité des positions d’équilibre. On choisit un courant I0= 14 A. La figure suivante représente la fonction F(z) en fonction de z pour z variant de 0 à 10 cm. mg = 0,005*9,8 = 0,049 N position d’équilibre z1 : si z augmente à partir de z1, l’intensité de la force de lévitation dirigée vers le haut augmente ; or le poids dirigé vers le bas reste constant. La résultante des forces est dirigée vers le haut et tend à écarter la sphère de sa position d’équilibre z1. Cette position d’équilibre est instable. position d’équilibre z2 : si z augmente à partir de z2, l’intensité de la force de lévitation dirigée vers le haut diminue ; or le poids dirigé vers le bas reste constant. La résultante des forces est dirigée vers le bas et tend à ramener la sphère de sa position d’équilibre z2. Cette position d’équilibre est stable. Etude de la sensibilité du gravimètre. Ce gravimètre est destiné à mesurer de petites variations dg de l’intensité du champ de pesanteur g. Le déplacement de la sphère est mesuré par un pont de condensateurs, qui permet d’être sensible à une variation dz de la position de la sphère de l’ordre de 10-11 m ! (inférieure à la taille d'un atome) Le principe de la mesure des variations de g consiste à opérer à altitude z0 fixée en faisant varier le courant I0. Ainsi lorsque g varie de dg , on fait varier le courant I0 d’une petite valeur dI0 de manière à ne pas changer la position d’équilibre stable repérée par z0. 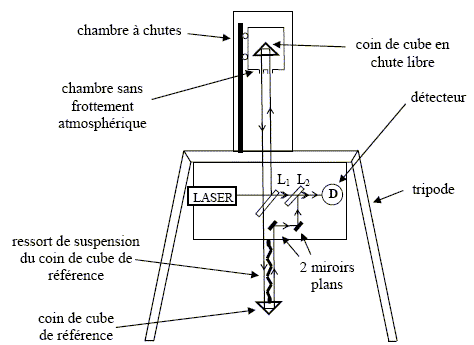Pour une intensité de la pesanteur égale à g et un courant I0 : mg = a z0/ (a2+z02)4 I20.(1) Pour une intensité de la pesanteur égale à g+dg et un courant I0+dI0 : m(g+dg) = a z0/ (a2+z02)4 (I0+dI0)2.(2) (2) / (1) donne : g+dg g = (I0+dI0)2 I20 1 + dg / g = (1+ dI0 / I0)2~ 1 + 2dI0 / I0 ; dg / g ~2dI0 / I0 ; si dg / g = 10-9 alors dI0= 4,5 10-9 I0 = 4,5 10-9 *14 =6,3 10-8 A, variation expérimentalement possible. Etude d’un gravimètre absolu à chute. On se propose dans cette partie d’étudier un gravimètre « balistique » qui permet de faire chuter pendant environ 200 ms et sur une distance de 0,20 m un objet possédant la forme d’un coin de cube dans une chambre à chutes où règne un vide poussé. L’objet en chute libre est un coin de cube dont la particularité est de réfléchir les rayons lumineux dans la même direction que le rayon incident. Il est placé dans une enceinte appelée « chambre sans frottement atmosphérique » dont le rôle est de placer le coin de cube en position haute et de le stopper délicatement à l’issue de son mouvement de chute libre. Cette chambre est pilotée par un dispositif électronique. L’ensemble coin de cube et « chambre sans frottement atmosphérique » est placé dans une chambre à chutes où règne un vide poussé ( pression de 10-4 Pa ). Un faisceau laser est émis, il est divisé en deux au niveau de la lame L1 (appelée lame semi réfléchissante). Le faisceau horizontal va directement au détecteur de lumière D. L’autre faisceau est dirigé vers le coin de cube en chute libre puis redescend vers un coin de cube de référence et est redirigé vers le détecteur de lumière D grâce à deux miroirs et la lame L2. Le coin de cube de référence est suspendu au bâti du dispositif par un ressort de très faible raideur. Le détecteur de lumière D délivre un signal électrique qui varie dans le temps au cours de la chute. L’étude de ce signal permet d’effectuer des mesures précises de la position du coin de cube. Une horloge atomique à rubidium fournit des mesures précises du temps. La fréquence délivrée par l’horloge vaut : 10000000,002 Hz. La longueur d’onde du laser est connue également avec une grande précision : par exemple l’une des valeurs utilisées vaut 632,99117754 nm. A partir des couples « position ; temps » caractérisant la loi horaire du mouvement du coin de cube, il est possible de déterminer l’accélération du mouvement et par là même l’intensité du champ de pesanteur. Bien que le principe de la mesure soit simple, la conception de ces appareils est très délicate car elle relève du domaine de la métrologie de très haute précision. Pourquoi fait-on le vide dans la chambre où se déroule la chute libre ? Le vide permet de supprimer les frottements sur les couches d'air : la chute est dite "libre". 10-4 Pa est une valeur très faible, comparée à la pression atmosphérique ~ 105 Pa. Le coin de cube de référence suspendu au bâti du dispositif par un ressort permet de diminuer l’influence de l’agitation « microsismique » due par exemple à l’activité industrielle ou humaine. Approximation d’un champ de pesanteur uniforme. On suppose dans cette question que l’accélération du champ de pesanteur est uniforme. Son intensité sera notée g0. On suppose que le mouvement du coin de prisme de masse m se réduit à un mouvement de translation selon la verticale Oz orientée vers le bas. A l’instant initial, la position est notée z0 et la vitesse v0. Equation horaire du mouvement donnant z en fonction de t. accélération lors d'une chute libre : a = g la vitesse est une primitive de l'aclération : v(t) = gt + v0 ; la position est une primitive de la vitesse : z(t) = ½gt2+v0t+z0. Chaque fois que le coin de cube parcourt une distance d = 3,165.10-4 m, l’horloge atomique donne la date. Chaque chute est ainsi échantillonnée en 600 couples de mesure « position ; temps ». En prenant g0 = 9,809 m.s-2, et en supposant z0 et v0 nulles, estimer la hauteur et la durée de la chute libre. h =599 d = 599* 3,165.10-4 =0,1896 m. h = ½g0t2 ; t = (2h/g0)½ = (2*0,1896 / 9,809)½ =0,1966 s. En réalité, les valeurs de z0 et v0 ne sont pas connues exactement, la détermination de g0 requiert au moins trois points de mesure. On note z1 la position du coin de prisme à la date t1 , z2 celle à la date t2 et z3 celle à la date t3. Exprimer g0 en fonction de t1, t2, t3, z1, z2, z3. z1 = ½g0t12+v0t1+z0 ; z2 = ½g0t22+v0t2+z0 ; z3 = ½g0t32+v0t3+z0 ; z2 -z1 =½g0(t2 -t1)(t2 +t1) + v0(t2 -t1) ; z3 -z1 =½g0(t3 -t1)(t3 +t1) + v0(t3 -t1) (z3 -z1) (t2 -t1) -(z2 -z1)(t3 -t1) = ½g0(t3 -t1)(t3 +t1)(t2 -t1) -½g0(t2 -t1)(t2 +t1)(t3 -t1) Or (t3 -t1)[ (t3 +t1)(t2 -t1) -(t2 -t1)(t2 +t1))= (t3 -t1)(t2 -t1)(t3 -t2) d'où : g0 = 2 [(z3 -z1) (t2 -t1) -(z2 -z1)(t3 -t1)] (t3 -t1)(t2 -t1)(t3 -t2) L’exploitation statistique de nombreuses séquences de chutes libres permet alors de déterminer une valeur de g0 et d’estimer l’erreur commise sur la détermination. Un exemple de mesure de g0 effectuée en janvier 2004 à Strasbourg donne après corrections : g0 = 980877798,2 + ou -4,4 µGal. Prise en compte du « gradient de pesanteur ». La valeur « brute » de l’intensité du champ de pesanteur obtenue après exploitation des couples « position ; temps » doit être corrigée de nombreux effets : influence des astres, valeur finie de la vitesse de propagation de la lumière, pression barométrique, mouvement des pôles, existence d’un « gradient de pesanteur »… On se propose d’étudier ce dernier effet en supposant que l’intensité g(z) du champ de pesanteur n’est pas uniforme et varie localement selon la loi : g(z) = g0 +g(z-z0) . La verticale Oz est orientée vers le bas ; g = 289,0 µGal m-1, valeur positive, g(z) augmente en se rapprochant du sol. g0 représente maintenant la valeur de g(z) au sommet z0 de la trajectoire. On choisit une hauteur h de chute égale à 19 cm ; déterminer la variation de g(z) entre le sommet et la base de la trajectoire. g(z) - g0 =g(z-z0) =289,0*0,19 =55 µGal. Cette valeur est bien supérieure à 4,4 µGal, erreur commise sur la détermination de g0 : il faut donc faire une correction. Equation différentielle décrivant le mouvement de translation du coin de cube. Ecrire la seconde loi de newton : md2z/dt2 = mg0 +mg(z-z0) ; d2z/dt2 = g0 +g(z-z0) avec z-z0 = ½g0t2 + v0t. d2z/dt2 = g0 +g(½g0t2 + v0t) 1ère intégration : dz/dt = g0t +½gg0t3 /3 +½gv0t2 + cste. à t = 0 la vitesse vaut v0 d'où : v0 = cste ; dz/dt = g0t +½gg0t3 /3 +½gv0t2 + v0. 2ème intégration : z = v0t +½ g0t2 +½gg0t4 /12 +½gv0t3/3 + cste. à t = 0 la position est z0 d'où : z0 = cste ; z = v0t +½ g0t2 +½gg0t4 /12 +½gv0t3/3 + z0.

retour -menu