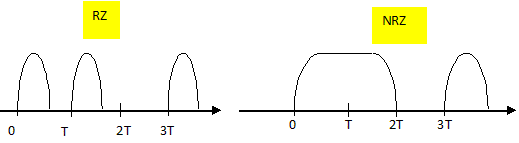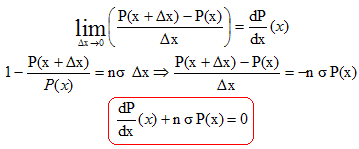codage numérique, injection du signal, atténuation dans une fibre : concours général 2006 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Codage numérique de l'information : Pour les télécommunications, l'information est généralement transmise dans les fibres optiques en format numérique, s'est à dire en code binaire, sous forme de 0 et de 1. La transmission de nombres impose donc une conversion de ceux-ci de la base décimale à la base binaire. En base binaire, il n'y a que deux chiffres : 0 et 1. Ainsi en base binaire, 2 s'écrit 10 ( 1*2 +0*1), 3 s'écrit 11 ( 1*2 +1*1), 4 s'écrit 100 ( 1*22 +0*2+0). Pourquoi les êtres humains utilisent-ils par défaut la base décimale pour exprimer les nombres ? Leurs mains ont dix doigts. Comment s'écrit le nombre 13 en base binaire ? 1*23 +1*22 +0*2*1 soit 1101. L'information codée en binaire est injectée chiffre par chiffre dans la fibre optique sous forme d'impulsion lumineuse avec la convention suivante : 0 pour une absence de lumière et 1 pour une présence de lumière. La transmission d'un chiffre 0 ou1, appelé "bits" dure un temps T. Il existe deux types de formats : - le RZ ( retour à zéro) où le signal lumineux redescend systématiquement et de façon quasi-instantanée à zéro entre chaque bit. Plus précisément, la transmission d'un bit sur une durée T s'effectue ainsi : indication de la valeur liée au chiffre transmis pendant un temps t0 puis retour à zéro pendant un temps T-t0. Pour la suite on supposer t0 =½T. - le NRZ ( non retour à zéro) où le signal garde la même valeur entre deux bits identiques. Quelle est la séquence de chiffres qui donne le signal lumineux de plus grande fréquence dans le format RZ ? Exprimer la fréquence en fonction de T. Succession de 1 : FRZ = 1/T Même question pour le format NRZ. alternance de 1 et de 0 : la période vaut alors 2T et la fréquence FNRZ = 1/(2T). On maximise le débit d'informations : - en utilisant le format NRZ : la fréquence maximale est le double de la fréquence maximale du format RZ ; pour une même bande passante, deux fois plus d'informations sont envoyées. - mais les effets non linéaires et la dispersion chromatique dans la fibbre incitent à choisir le formar RZ où les impulsions lumineuses ont toutes la même période quelle que soit la séquence transmise. Injection du signal. 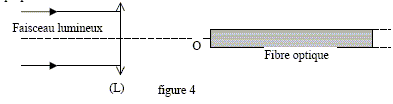On injecte la lumière dans la fibre optique à l'aide d'une lentille mince convergente L de diamètre D et de distance docale f. Celle-ci est éclairée par un faisceau rectiligne incident parallèle à l'axe optique. Où doit on mettre la lentille pour que le faisceau converge au point O, situé à l'entrée de la fibre ? La distance lentille-entrée de la fibre O, doit être égale à la distance focale f. On appelle puissance lumineuse la puissance transportée par l'onde lumineuse. On peut montrer à l'aide des lois de l'électromagnétisme que la lumière ne peut pas passer entièrement dans la fibre. A l'interface air / verre, il passe uniquement une fraction a<1 de la puissance lumineuse, donnée par : a = 4 n1/(n1+1)2. Que devient la fraction non transmise dans la fibre ? La lumière non transmise dans la fibre est réfléchie par la face d'entrée de la fibre. Pour les applications numériques on prendra n1 = 1,50. Pour l'étude des fibres optiques, il est d'usage de raisonner en décibels. La variation de puissance entre un poit A et un point B est quantifiée par la grandeur GdB= 10 log (PB/PA), exprimée en dB ( décibel), où P désigne la puissance lumineuse. Calculer la perte de puissance lors de l'injection de la lumière dans la fibre. GdB= 10 log a ; a = 4 n1/(n1+1)2 = 4*1,5 /2,52 =0,96. GdB = 10 log 0,96 = -0,18 dB. A la sortie de celle-ci, il y a à nouveau perte de puissance à l'interface verre / air de même valeur qu'à l'entrée. Calculer la perte de puissance totale en dB entre l'entrée et la sortie de la fibre ( on néglige dans cette question les pertes à l'intérieur de la fibre). A l'entrée GdB = 10 log Ptransmise /P totale ; Ptransmise = P totale 10 0,1GdB à la sortie GdB = 10 log Psortante /P transmise ; Psortante = P transmise 10 0,1GdB = P totale 10 0,1GdB *10 0,1GdB Psortante = P totale 10 0,2GdB ; GdB totale = log (Psortante / P totale ) = 2 GdB = -0,36 dB. Les pertes exprimées en dB s'ajoutent. 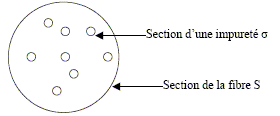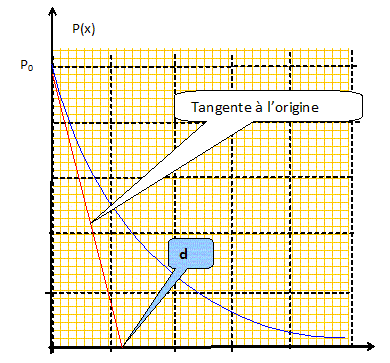Atténuation du signal. Une fibre optique n'est pas rigoureusement transparente. Elle contient des impuretés qui vont diffuser la lumière hors de celle-ci. La puissance lumineuse va donc décroître au cours du trajet. Le modèle simple suivant propose d'étudier cette décroissance. On note n la densité volumique des impuretés dans un m3, supposées toutes identiques ( petite boule sur la figure 5). On note P(x) la puissance lumineuse à l'abscisse x et l'on raisonne sur une tranche de longueur Dx comprise entre x et x+Dx. L'aire de la section de la fibre vaut S. Donner le nombre d'impuretés N dans la tranche en fonction des données. Volume de la tranche dV= SDx ; N= ndV ; N = nSDx. La figure suivante montre la tranche vue depuis l'amont de la fibre. Une impureté a une section apparente notée s ( appelée section efficace). Toute lumière arrivant sur une impureté et diffusée et donc ne franchit pas la tranche. A contrario, la lumière passant à côté des impuretés atteint l'extrémité de celle-ci. En supposant que la lumière se propage rectilignement selon Ox et que la puissance est répartie uniformément sur une section de la fibre, calculer la fraction r =P(x+Dx) / P(x) de la puissance qui arrive à traverser la tranche en fonction de S, s et N. On néglige le recouvrement éventuel des sections apparentes des impuretés. section apparente des impuretés : Ns = nSs Dx. P(x+Dx) est proportionnelle à S-Ns = S(1-ns Dx) ; P(x) est proportionnelle à S. r = P(x+Dx) / P(x) =1-Ns/S = 1-ns Dx. En faisant tendre Dx vers zéro, établir l'équation différentielle vérifiée par P(x) faisant intervenir les constantes s et n. Solutions de cette équation : on pose d = 1/ (ns), distance caractéristique d'atténuation de la puissance dans la fibre. P(x) = P(x=0) exp(-x/d) = P0 exp(-x/d). Montrer que la perte de puissance lumineuse dans la fibre exprimée en dB décroît de manière linéaire en fonction de l'abscisse x. ln (P(x) /P0 ) = -x/d ; passage au logarithme décimal ln = 2,3 log 2,3 log (P(x) /P0 ) = -x/d ; log (P(x) /P0 ) = -x/ (2,3d ) ; 10 log (P(x) /P0 ) = -10 x/ (2,3d ) ; GdB = -10 x/ (2,3d ). Pour du verre standard ( verre à vitre) l'atténuation est de l'ordre de 0,1 dB/mm, valeur beaucoup trop grande pour les télécommunications. Les fibres optiques sont fabriquées à partir d'un verre ultra-pur, dont l'atténuation peut descendre à 0,2 dB /km. Pour un câble électrique coaxial, l'atténuation du signal électrique pour les fréquences utilisées dans les télécommunications à très haut débit est au mieux de 10 dB/km. En supposant que le signal doit être ré-amplifié dès que sa puissance est inférieure à 1% de sa valeur d'émission, combien faut t-il d'amplificateurs pour une liaison Paris Marseille ( distance 750 km) dans le cas d'une liaison par fibre optique ? GdB = 10 log 0,01 = -20 dB ; l'atténuation est 0,2 dB/km Il faut un amplificateur tous les : 20 / 0,2 = 100 km soit 7 amplificateurs. Même question pour le câble électrique. L'atténuation est 10 dB/km ; il faut un amplificateur tous les 2 km ( soit 375 au total : le côut et la maintenance vont être élevés) L'atténuation dans une fibre optique dépend de la longueur d'onde l ( par l'intermédiaire du terme s ). On recherche des longueurs d'onde qui subissent l' atténuation la plus faible. Même en absence d'impureté, l'atténuation n'est pas nulle. Une des causes est la diffusion Rayleig : tout atome diffuse nécessairement la lumière. On montre que la puissance diffusée est proportionnelle à 1 / l 4. La diffusion Rayleig incite t-elle à travailler dans l'ultra-violet (UV), le visible ou l'infrarouge ( IR) ? Les longueurs d'onde de l'infrarouge sont supérieures à celle du visible et de l'UV) : dans l'IR la puissance diffusée sera plus faible que dans le visible ou l'UV. La figure suivante représente l'atténuation endB/km dans les fibres optiques en verre en fonction de la longueur d'onde. Si vous aviez à utiliser une fenètre spectrale ( intervalle de longueur d'onde) de 0,1µm pour les télécommunications optiques, laquelle choisiriez-vous ? Dans quel domaine optique se trouve t-on ? L'atténuation doit être la plus faible possible : la courbe présente un minimum vers 1,6 µm ; cette valeur est supérieure à 0,8 µm : elle appartient à l'IR.

retour -menu