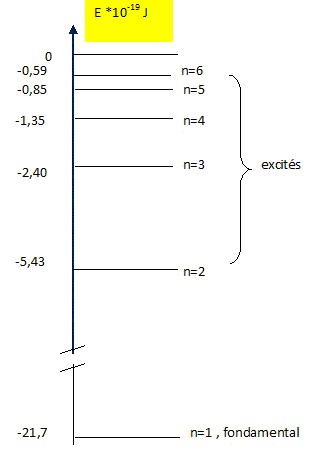atome d'hydrogène: séries de Lyman et Balmer d'après IMRT En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Les éries de Lyman et de Balmer du spectre de l'atome d'hydrogène sont émises au cours des transitions quantiques de l'atome d'hydrogène, respectivement vers le premier niveau ( niveau fondamental) et vers le second niveau ( 1er niveau excité). L'énergie de l'atome dans l'état fondamental est E0 = -13,6 eV. Par convention, l'énergie de l'atome est nulle lorsque l'électron et le proton sont infiniment éloignés l'un de l'autre ( ionisation). On donne les longueurs d'onde de la série de Lyman : 1ère raie 121,6 nm 2ème raie 102,6 nm 3ème raie 97,3 nm 4ème raie 95 nm 5ème raie 93,8 nm Calculer en joule l'énergie des niveaux 2, 3, 4, 5 et 6 de l'atome d(hydrogène . Energie du photon = En-E0 = hc / l. avec E0 = -13,6 *1,6 10-19 = -2,176 10-18 J E2-E0 = 6,62 10-34 * 3 108 / 121,6 10-9=1,633 10-18 J E2= E0 +1,633 10-18 = ( -2,176 +1,633) 10-18 ; E2= - 5,43 10-19 J. E3-E0 = 6,62 10-34 * 3 108 / 102,6 10-9=1,936 10-18 J E3= E0 +1,936 10-18 = ( -2,176 +1,936) 10-18 ; E3= - 2,40 10-19 J. E4-E0 = 6,62 10-34 * 3 108 / 97,3 10-9=2,041 10-18 J E4= E0 +2,041 10-18 = ( -2,176 +2,041) 10-18 ; E4= - 1,35 10-19 J. E5-E0 = 6,62 10-34 * 3 108 / 95,0 10-9=2,091 10-18 J E5= E0 +2,091 10-18 = ( -2,176 +2,0917) 10-18 ; E5= - 0,85 10-19 J. E6-E0 = 6,62 10-34 * 3 108 / 93,80 10-9=2,117 10-18 J E6= E0 +2,117 10-18 = ( -2,176 +2,117) 10-18 ; E6= - 0,59 10-19 J. Donner la relation existant entre ces différentes énergies et E0. En = E0 / n2 avec n : nombre quantique principal. n valeur expérimentale ( J) valeur calculée ( J) 2 - 5,43 10-19 -5,44 10-19 3 - 2,40 10-19 -2,417 10-19 4 - 1,35 10-19 -1,36 10-19 5 - 0,85 10-19 -0,87 10-19 6 - 0,59 10-19 -0,60 10-19 Représenter schématiquement ces niveaux. Calculer la longueur d'onde de la transition la moins énergétique de la série de balmer. A quel type de photon ( radio, IR, visible, UV, X, gamma) appartient-elle ? Transition vers le second niveau E2. Tansition la moins énergétique : E3-E2 = (5,43-2,40) 10-19 = 3,03 10-19 J l = hc /( E3-E20). l = 6,62 10-34 * 3 108 / 3,03 10-19 =6,55 10-7 m = 655 nm. ( visible)

retour -menu