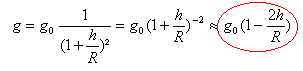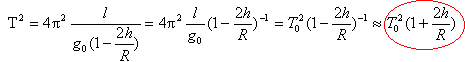|
concours kiné A P Paris /01.
|
|||
|
Un solide ponctuel de masse m est suspendu à un fil métallique OA de longueur l et de masse négligeable. L'ensemble oscille dans un plan vertical. A un instant on lance le solide vers le bas avec un vecteur vitesse V0, alors que le solide est écarté de sa position d'équilibre d'un angle q0. V0 est perpendiculaire à la direction du fil. Toute l'étude sera faite dans le référentiel géocentrique supposé galiléen. La rotation de la terre est négligée. Période du pendule :
corrigé |
|||
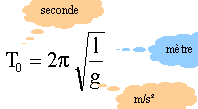
si le pendule bat la seconde, alors la période est T0=2s. l =T0² g / (4p²) = 4 *9,8 / (4*3,14²) = 0,994 m. dans l'expression de la période g intervient au dénominateur : si g diminue alors T augmente g figure sous le radical: si g est divisé par 4, alors la période double. expression de g : expression de g au niveau du sol, altitude zéro: (G est la constante de gravitation, M la masse de la terre et R le rayon terrestre) g0 = GM / R² ou encore GM=g0R². expression de g à l'altitude h: g= GM / (R+h)² = g0R² / (R+h)² on divise par R² numérateur et dénominateur: onutilise le résultat ( 1 +e)n voisin de 1+ne si e petit devant1.
expression de la nouvelle période: T est supposée proche de T0 donc T+T0 voisin de 2T0.
T² / T0² -1 = 2h/R (T²-T0²) / T0² = 2h / R (T-T0)(T+T0) / T0² voisin de 2 (T-T0) /T0 = 2h / R soit (T-T0) /T0 =h / R. h/R est positif, donc T est plus grand que T0 : l'horloge retarde.
retour - menu |