|
concours Kiné Nantes 2002 |
|||||||||||||||||
|
|||||||||||||||||
|
On considère un système oscillant constitué d'un solide S de masse m= 200 g, fixé à l'extrémité d'un ressort de raideur k = 2,5 N/m. L'ensemble est astreint à se déplacer sur un axe Ox horizontal et le centre d'inertie G du solide S se situe à l'origine O de l'axe lorsque le système est au repos. On communique une énergie mécanique initiale E0=2 mJ au solide ; l'énergie potentielle de pesanteur étant choisie nulle dans le plan horizontal dans lequel se déplace M. Le système se met alors à osciller librement. On considérera que le ressort reste toujours à spires non jointives. 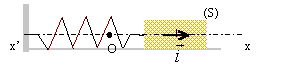 Dans tout le problème on établira l'expression de la grandeur demandée avant d'effectuer l'application numérique. 1ère partie : oscillateur sans amortissement A l'instant initial, le solide est placé en x= d= +2 cm et on lui communique dans cette position une vitesse v0 dans le sens de l'axe Ox.
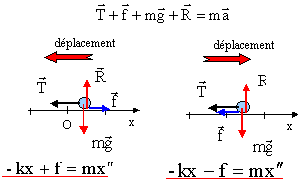
2ème partie : oscillateur soumis à un frottement solide. On considère le même oscillateur soumis à une force de frottement f colinéaire au vecteur vitesse et de norme constante f = 7,5 mN. A l'instant initial, le solide est écarté de sa position d'équilibre jusqu en x=x0 positif et on l'abandonne sans vitesse initiale( son énergie initiale est E0= 2 mJ).
corrigé l'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle élastique. 2 10-3 = ½mv² + ½kx² dériver par rapport au temps : remarque (u²)' = 2 u u' 0 = ½ m 2 v v' + ½ k 2 x x' mv v' + k x x' = 0 avec v = x' et v' = x'' m x' x" + kx x' =0 soit mx" + kx = 0 soit x" + w0 ² x = 0 avec w0 ² = k/m. w0
= racine carrée ( 2,5 / 0,2 ) =
3,54 rad/s ;
T0 = 2p / w0
=6,28 / 3,54 = 1,776
s.
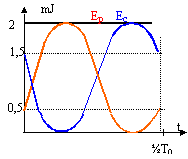
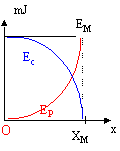
énergie cinétique initiale 2-0,5 = 1,5 mJ 1,5 10-3 = ½mv0² d'où v0 = 0,122 m/s. Lorsque x = Xm alors l'énergie mécanique est sous forme potentielle élastique : 2 10-3 = ½k Xm² d'où Xm = 0,04 m = 4 cm. Lorsque x=0 l'énergie est entièrement sous forme cinétique : 2 10-3 = ½m Vm²
d'où Vm = 0,141
m/s.
à t = 0 x = 0,02 d'où 0,02 = 0,04 cosf soit cosf = 0,5 deux solutions f = + 1,05 rad et f = - 1,05 rad expression de la vitesse x' = v = - Xm w0 sin(w0t + f) = -0,1416sin ( w0t + f) or à t=0, la valeurf = - 1,05 rad conduit à v0 = -0,1416 sin (-1,05) = 0,122 m/s ( accord avec la valeur trouvée) or à t=0, la valeurf = 1,05 rad conduit à v0 = -0,1416 sin (1,05) = - 0,122 m/s ( désaccord avec la valeur trouvée) x(t) = 0,04 cos(3,54 t -1,05 ).
énergie potentielle élastique : Ep = ½kx² = 1,25 *0,04² cos²(3,54 t -1,05 ). Ep = 2 cos²(3,54 t -1,05 ) en mJ. (courbe rouge) énergie cinétique : Ec = ½ mv² =0,1 * 0,141² sin² (3,54 t -1,05 ). Ec = 2
sin²(3,54 t -1,05 ) en mJ.(courbe
bleue) à t=0 l'énergie mécanique est sous forme potentielle ½kx0² = 2 10-3 d'où x0 = racine carrée (4 10-3 / 2,5) = 0,04 m = 4 cm. la force de frottement est toujours opposée au déplacement
1ère demi période ( déplacement de droite à gauche ) x"+ k / m x = f / m (1) 2ème
demi période
( déplacement de gauche à droite ) x"+ k / m x
= -f /m (2)
avec
w0²
= k/m
solution particulière de (1) : x = f / k solution générale de (1) : x(t) =A cos (w0t+F) + f / k d'où g = f / k = 7,5 10-3 / 2,5 = 0,003 m. vitesse : x'(t) = -Aw0 sin (w0t+F) ; v' (t=0) = -Aw0 sin (F) =0 d'où F =0 ou F =p. F =0 donne x(t=0) = A cos (0) + 0,003 = x0 = 0,04 d'où A = 0,037 m. F =p donne x(t=0) = A cos (p) + 0,003 = x0 = 0,04 d'où A = -0,037 m. or A doit être positif, donc F =p n'est pas à retenir. x(t) =0,037 cos (w0t) + 0,003 avec w0= 3,54 rad/s. x( t = T0/2)= 0,037 cos p +0,003 = -0,034 m. x( t = T0/4)= 0,037 cos (0,5p) +0,003 = 0,003 m. vitesse : x'(t) =-0,037*3,54 sin(w0t ) = -0,13 sin(w0t ) =0,13 sin(w0t +p) v(( t = T0/2) = 0,13 sin (2p) = 0 v(( t =
T0/4) = 0,13 sin (0,5p+
p) =
-0,13
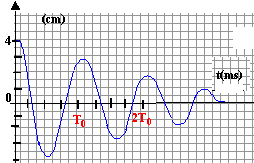
les conditions initiales sont différentes du cas précédent, donc les constantes d'intégration sont différentes. solution générale de x"+ w0² x = 0 : x(t) = B cos (w0(t-T0/2)+F1) solution particulière de (1) : x = -f / k solution générale de (1) : x(t) =B cos (w0(t-T0/2)+F1) - f / k d'où g = f / k = 7,5 10-3 / 2,5 = 0,003 m. et e = -1 vitesse : x'(t) = -Bw0 sin (w0(t-T0/2)+F1) ; v' (t=T0/2) = -Bw0 sin (F1) =0 d'où F1 =0 ou F1 =p. F1 =0 donne x(t=T0/2) = B cos (0) - 0,003 = -0,034 d'où B = -0,031 m. or B doit être positif, donc F1 =0 n'est pas à retenir. F1 =p donne x(t=T0/2) = B cos (p) - 0,003 = -0,034 d'où B = 0,031 m. x(t) =0,031 cos (w0t) - 0,003 avec w0= 3,54 rad/s. x( t = T0)= 0,031 cos 0 -0,003 = 0,028 m. à chaque demi période l'amplitude diminue de 0,006 m à t = n T0/2, l'amplitude aura diminué de : 0,006 n x (t = n T0/2) = 0,04- 0,006 n. arrêt des oscillations à la date t = 0,04/ 0,006 = 6,66 T0/2 = 3,33 T0. à la fin de chaque demi-période le ressort est comprimé ou allongé au maximum : celui ci emmagasine de l'énergie potentielle élastique qui lui permet de repartir dans l'autre sens.
à t = T0 : énergie mécanique = énergie potentielle élastique = 0,5 *2,5* 0,028² = 0,98 mJ pertes : 2-0,98 = 1,02 mJ.(soit environ 51 %)
retour - menu |