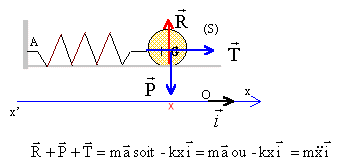Aurélie 03/02
mouvement d'une bille sur un rail

concours kiné Hte Normandie

suite-->acide base

Google

Soit un ressort à spires non jointives de constante de raideur k. L'une des extrémités de ce ressort est fixée à un support, l'autre est solidaire d'une bille de polystyrène de masse M. La masse du ressort est négligeable devant M. Ce ressort et la bille peuvent coulisser sans frottement le long d'un rail horizontal. Un expérimentateur tire la balle vers A sur une longueur L puis la relâche sans vitesse initiale à un instant pris pour origine des dates. A la date t1 la bille passe pour la deuxième fois la position d'allongement nul du ressort notée N. Elle se détache alors du ressort pour poursuivre son chemin sur le rail. On admet que la bille glisse sur le rail sans tourner sur elle même. Entre les points A et B du rail un dispositif charge la bille. Entre O et O' une différence de potentiel tend à freiner la progression du mobile. On admet que la bille ne rencontre aucun frottement le long du rail DD' et que le dispositif entre O et O' est comparable à un condensateur plan ( la bille sera considérée comme ponctuelle dans le condensateur).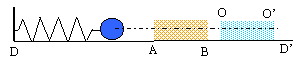

 

  1. Exprimer en fonction de k et de M la période du mouvement oscillatoire avant le décrochage de la bille puis la calculer.
  2. En appliquant le théorème du centre d'inertie que l'on rappellera ( faire un schéma précis sur lequel figurera l'axe orienté, l'origine de cet axe étant prise en N).
    - Retrouver l'équation différentielle qui caractérise le mouvement avant le décrochage ( en expression littérale)
    - Donner l'équation horaire littérale de ce mouvement.
    - Donner l'équation horaire du mouvement en ayant calculé tous les paramètres.
  3. Exprimer puis calculer la date t1.
  4. Exprimer puis calculer la vitesse V1 du mobile à la date t1.
  5. Indiquer la nature du mouvement le long du trajet NO ainsi que la valeur de la vitesse en O notée V.
  6. La bille finit par s'arrêter sur le rail dans la partie OO' à une distance d de O, avant de repartir en sens inverse. On admettra que la force d'origine électrostatique subie par la bille entre O et O' est de même valeur que la résultante des forces subies par celle-ci à l'origine des dates.
    -Exprimer d en fonction de L puis calculer d.
  7. E étant la valeur du champ électrique entre O et O', exprimer puis calculer la valeur absolue de la charge emmagasinée par la bille entre A et B.
  8. En fait d est égal à 25 cm. Trouver la valeur de la vitesse en O sachant que la seule partie du rail présentant des frottements est AB.

    Données : k= 0,01 N/m ; M= 10 g ; L= 1m ; E = 10 kV ;  

 

corrigé

période de l'oscillateur élastique : T= 2p racine carrée (M/k)

M= 0,01 kg ; k = 0,01 N/m ; T = 6,28 s.
poids et action du support sont opposées

x: abscisse de G

équation différentielle du mouvement de G

x" + w² x = 0 avec w ² = k/m = 0,01 / 0,01 = 1

w = 1 rad/s.
solution de cette équation différentielle : x = xmax cos( w t+j)

xmax correspond à l'amplitude c'est à dire à L = 1 m.

à l'instant initial t=0, l'abscisse x est égale à L :

x(t=0 ) = L = L cos (0+j) soit L = L cos(j)

en conséquence j=0 et x(t) = Lcos(w t) = cos (t).

date t1 :

à la date t1, l'abscisse de G est nulle pour la seconde fois

x(t1) = 0 = cos( t1)

t1 = (2k+1) p/2

k = 0 correspond au premier passage en x=0, la bille se dirigeant vers la gauche

k=1 correspond au second passage en x=0, la bille se dirige vers la droite.

t1 = 3p/2 = 4,71 s ( les 3/4 de la période)

entre N et O :

en absence de frottement la bille est soumise à deux forces opposées: son poids et l'action du rail.

la bille est pseudo-isolée et d'après le principe d'inertie le mouvement du centre de gravité de la bille est rectiligne uniforme.

la vitesse en O a la même norme que la vitesse en N

vitesse en N ( date t1).

la vitesse est la dérivée de l'abscisse par rapport au temps: v N= -sin (t1) = -sin (3p/2) = 1 m/s.

distance d :

la force électrostatique est égale à la tension du ressort à la date t=0 soit F = kL = 0,01*1 = 0,01 N.

poids et action du sol sont perpendiculaires à la vitesse : seule la force électrique travaille entre O et O'

le travail de cette force est résistant (freinage); de plus force électrique et déplacement sont colinéaires

d'où W = - kLd = -0,01 d.

variation d'énergie cinétique entre O et O' (arrêt) : - ½ mv²

théorème de l'énergie cinétique entre O et O' : -½mv² = -kLd

d = ½mv² / (kL) = 0,5 * 0,01 * 1² / (0,01*1) = 0,5 m.

charge :

F=|q| E avec F= 0,01N et E = 104 V/m

|q| = 10-6 C.

vitesse réelle en O :

d = ½mv² / (kL)

si la distance d est divisée par deux, alors le carré de la vitesse est divisé par deux

la vitesse précédente en O est donc divisée par racine carrée de 2

v= 0,7 m/s.

retour - menu