concours kiné Berck 03

radioactivité Le technécium 99 est un émetteur b- dont la durée de vie est très grande. Un échantillon de technécium voit son activité divisée par 5 en 490 000 ans. On admettra qu'un échantillon radioactif n'est plus dangereux au bout d'un temps égal à 10 fois sa demi-vie. - Déterminer le temps (en milliers d'années) au bout duquel l'échantillon peut-être considéré comme inoffensif. 980 ; 1240 ; 1960 ; 2110 ; 2300 ; 2650. Parmi les affirmations suivantes, combien y en a-t-il d'exactes ? - Parmi deux échantillons radioactifs possédant le même nombre initial de noyaux radioactifs, celui qui a la demi-vie la plus courte a une plus grande activité. - Au bout d'un temps égal à 4 fois sa demi-vie, l'activité d'un échantillon d'un isotope radioactif a été divisée par 16. - L'unité de la constante radioactive l est la seconde. - La tangente à une courbe de décroissance radioactive à l'instant t=0 coupe l'axe des abscisses au point t = T/ln 2 où T désigne la demi-vie de l'isotope radioactif considéré. - L'activité d'un échantillon à un instant donné est proportionnelle au nombre de noyaux radioactifs contenus dans cet échantillon à l'instant considéré. Dans un réacteur nucléaire les noyaux d'uranium 235 subissent la fission sous le choc d'un neutron lent. On considerera la réaction suivante : 23592U+01n-->14054Xe + 94xSr + y 01n Données : masse d'un neutron : 1,00866 u ; masse 23592U : 234,99332 u ; masse 94xSr :93,89446 u ; masse 14054Xe : 139,89194 u ; 1 u = 1,66054 10-27 kg ; c = 3 108 m/s ; 1eV = 1,6022 10-19 J ; NAvogadro = 6,022 1023 mol-1; pouvoir calorifique du pétrole : P=43 MJ/kg ; masse molaire de l'uranium 235 : M=235 g/mol. Un réacteur nucléaire fourni une puissance électrique moyenne de 950 MW. On suppose que cette puissance électrique fournie par le réacteur est constante dans le temps. Le rendement de la transformation énergie nucléaire en énergie électrique est de 35 %. - Après avoir équilibré l'équation bilan précédente, donner les valeurs de x et de y. - Calculer l'énergie libérée par la fission d'un noyau d'uranium 235 suivant la réaction proposée. - On admettra que toutes les réactions de fission produisent la même énergie que la précédente. - Déterminer la masse ( en kg) d'uranium 235 consommée par le réacteur en une journée. - Déterminer la masse de pétrole ( en tonnes) qu'il faudrait brûler pour produire la même énergie qu'un kg d'uranium. - Calculer la date Dt ( en heures et minutes) nécessaire pour consommer un kilogramme d'uranium 235 dans ce réacteur. corrigé A = A0 e-l t avec l T= ln2 ln (A0 / A) = l t avec A0 / A = 5 si t = 4,9 105 ans  ln 5 =l*4,9 105 soit l= 3,284 10-6 an-1. T = ln2 / l= 0,693 / 3,284 10-6 = 2,11 105 ans 10 T = 2,11 106 ans = 2110 milliers d'années. * N= N0 e -lt. activité A = -dN/dt = -N0 (-l) e -lt=lN ou bien à t=0 : A0 = lN0. or l T=ln2 ( T période ou demi-vie ; l constante radioactive) A0 = N0ln2 / T l'activité initiale est d'autant plus grande que la demi-vie est plus courte. * l'activité est divisée par 24 = 16 au bout de 4 périodes. * l'unité de la constante radioactivelest l'inverse d'un temps. * dN/dt = N0 (-l) e -lt; à l'instant initial dN/dt = -N0l. ( coefficient directeur de la tangente à la courbe de décroissance radioactive à t=0) Cette tangente passe également par le point (0, N0) d'où son équation : N=-N0l t + N0. N= 0 si t = 1/l . or l T=ln2 soit t = 1/l = T / ln 2. *A= lN l'activité à la date t est proportionnelle au nombre de noyaux présents à l'instant t 23592U+01n-->14054Xe + 94xSr + y 01n conservation de la charge : 92 = 54+x d'où x = 38 conservation du nombre de nucléons : 235+1=140+94+y d'où y=2. variation de masse |Dm|=|139,89194+93,89446+1,00866-234,99332|=0,19826 u soit 0,19826*1,66 10-27 = 3,29 10-28 kg énergie libérée par fission : E=Dmc² = 3,29 10-28 *(3 108)² =2,96 10-11 J 2,96 10-11/ 1,6 10-19 = 1,85 108 eV = 185 meV. énergie libérée par 235 g d'uranium 235 ( une mole) : 2,96 10-11*6,02 1023 = 1,78 1013 J /mol énergie libérée par kg d'235 U : 1,78 1013 *1000 / 235 = 7,58 1013 J/kg. énergie nucléaire libérée en 24 h : puissance (W) * temps (s) / rendement 9,5 108 *24*3600 / 0,35 = 2,345 1014 J masse d'235 U consommée par jour : 2,345 1014 / 7,58 1013 = 3,1 kg. 1 kg d'uranium libère : 7,58 1013 J diviser par le pouvoir calorifique du pétrole 4,3 107 J/kg : 7,58 1013 / 4,3 107 =1,76 106 kg = 1760 tonnes de pétrole. durée pour consommer 1 kg d'uranium : 3,1 kg consommé par 24 h soit 24 / 3,1 = 7 H 45 min.

chute, satellite, oscillateur Une bille d'acier sphérique de rayon r= 4 cm tombe verticalement dans l'air à vitesse constante V. l'air exerce sur la bille une force de frottement fluide qui a pour expression F=Kpr² rair V² où K est une constante. On négligera la poussée d'Archimède s'exerçant sur la bille. rair = 1,29 kg/m3 ; racier = 7800 kg/m3 ; K=0,2. - Déterminer l'énergie cinétique (J) de la bille en arrivant au sol . 165 ; 2,47 ; 2,88 ; 3,15 ; 3,35 ; 3,62. La période de révolution d'un satellite en orbite circulaire autour de la terre est T= 5548 s. On place le satellite sur une orbite circulaire, la période du satellite augmente de 8%. G= 6,67 10-11 SI ; MT= 5,98 1024 kg ; RT= 6370 km. - Déterminer l'altitude (en km) du satellite sur sa nouvelle orbite. 348 ; 532 ; 762 ; 896 ; 1023 ; 1230. Un solide S de masse m glissant sans frottement sur une tige horizontale, est accroché à un ressort idéal de raideur k dont l'autre extrémité est fixée à un support. La position du centre d'inertie G du solide à l'équilibre constitue l'origine O de l'axe des abscisses. On écarte le solide de sa position d'équilibre, de 5 cm dans le sens des abscisses et on le libère sans vitesse initiale. L'origine des temps sera prise au premier passage du centre d'inertie à la position d'équilibre. L'énergie du système {solide + ressort} est constante et égale à 20 mJ. A la date t= 50 ms, l'énergie potentielle élastique du système est de 4,9 mJ. - Déterminer la masse ( en g) du solide. 50 ; 100 ; 150 ; 200 ; 250 ; 300. corrigé valeur de la vitesse constante, donc mouvement uniforme; de plus le mouvement est rectigne. Le principe d'inertie ( 1ère loi de Newton) indique que la somme des forces appliquée s à la bille est nulle. valeur du poids =valeur des frottements soit mg = Kpr²rair V² avec m (kg ) =masse volumique acier fois volume de la bille (m3) m= racier 4pr3/3 racier 4pr3/3 g= Kpr²rair V² d'où V² = 4rracier g / (3Krair) V² = 4* 4 10-3 *7800*9,8 / (3*0,2*1,29) = 1580,16 m²/s² masse de la bille = racier 4pr3/3 = 7800*4*3,14*(4 10-3)3/3 = 2,09 10-3 kg énergie cinétique = ½mV² = 0,5 *2,09 10-3 *1580,16 = 1,651 J. Nouvelle période T1 = 1,08 T = 1,08*5548 = 5991,84 s. 3ème loi de Kepler : T²/h3 =4p²/(GM) 4p²/(GM) = 9,887 10-14.   T1²/h13 = 9,887 10-14 d'où h13 = T1² / 9,887 10-14 = 3,63 1020. h1 = 7134,3 km; il suffit de retrancher le rayon terrestre (6370 km) pour obtenir l'altitude par rapport au sol : 764 km. Energie mécanique EM= énergie cinétique Ec + énergie potentielle élastique Ep EM= ½mv² + ½kx² si x= 0,05 ( l'amplitude) Em est sous forme d'énergie potentielle élastique : 0,02 = ½ka² k = 2*0,02 / (0,05)² = 16 N/m. à t = 50 ms : ½kx² = 4,9 10-3 J d'où x² = 9,8 10-3 /16= 6,125 10-4 m² ; x= 2,475 10-2 m. x(t) = a sin (w0t) à t = 0 x(t=0) doit être nul. x(t=0,05 ) = 2,475 10-2 = 0,05 sin(w0*0,05) sin(w0*0,05) = 0,495 = sin 0,518 (rad) soit w0*0,05 =0,518 w0= 0,518/0,05 = 10,356 rad/s. or w²0= k /m d'où m = k / w²0= 16/ 10,356² = 0,150 kg = 150 g.

solénoïde, dipôle RL, résistor en dérivation   On place une aiguille aimantée au centre d'un solénoïde d'axe horizontal comprenant 450 spires par mètre. L'axe du solénoïde est perpendiculaire à la direction nord-sud que prend l'aiguille aimantée dans le champ magnétique terrestre. L'aiguille tourne d'un angle a lorsqu'on fait passer dans les spires un courant d'intensité I=18mA. La valeur de la composante horizontale du champ magnétique terrestre vaut : BH= 2 10-5 T ; m 0 = 4 p 10-7 SI. - Déterminer la valeur de l'angle a (en degré) dont l'aiguille a tourné. 27 ; 32,2 ; 43,8 ; 63 ; 69,2 ; 74,2. 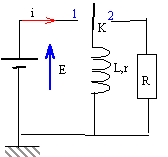On considère le circuit ci-dessous L'interrupteur K est placé en position1 jusqu'à obtention du régime permanent. On bascule ensuite K en position 2. Cet instant est considéré comme instant initial. R= 33 ohms ; E= 12 V ; L= 58 mH ; r= 27 ohms. - Déterminer la valeur de l'énergie stockée dans la bobine en mJ au bout de 1,4 ms. 17 ; 24 ; 36 ; 45 ; 58 ; 64. Une bobine d'inductance L et de résistance r=5,4 ohms est parcourue par un courant dont l'intensité varie commel'indique la figure.  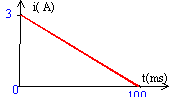- Déterminer la valeur de L ( mH) pour que la tension aux bornes de la bobine soit nulle à la date t=50 ms. 130 , 180 ; 220 ; 270 ; 330 ; 390. données : tension aux bornes d'un moteur U=E' + r'i ; E=6 V ; r = 8 ohms ; R1= 10 W ; R2 = 15 W ; R3 = 17 W ; E'=2 V ; r' = 5 W. 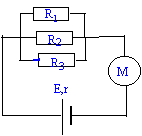- Calculer la valeur de l'intensité i (mA) du courant délivré par le générateur. 135 ; 229 ; 245 ; 297 ; 349 ; 378. On considère un générateur de fem E et de résistance interne r. Il fournit un courant d'intensité i et la tension à ces bornes est de 5,4 V. En une heure de fonctionnement ce générateur fournit au circuit une énergie de 9,4 kJ. Le rendement électrique de ce générateur est h=0,85. - Déterminer la valeur de la fem E ( V) de ce générateur . 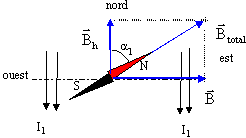5,4 ; 6,4 ; 7,4 ; 8,4 ; 9,4 ; 10,4 corrigé  B= m0nI =4p 10-7 *450*18 10-3 = 1,02 10-5 T. tan a1 = B/Bh = 1,02 10-5 / 2 10-5 = 0,51 et a1 =27°. t = L/ (R+r) =0,058 / (33+27) = 0,967 ms. I0 = E/r = 12/27 = 0,444 A i(t) = I0 e-t/t = 0,444 e -1,4 / 0,967 = 0,104 A énergie stockée dans la bobine : E = ½Li² E = 0,5*0,058 * 0,104² = 3,16 10-4 J = 0,316 mJ = 316 mJ. coefficient directeur de la droite di/dt = - 3/0,1 = -30 A/s ; i(t= 50 ms) = 1,5 A ( lecture graphe) tension aux bornes de la bobine : u = L di/dt + ri =0 L(-30) + 5,4*1,5 = 0 d'où L= 0,27 H = 270 mH. les résistors sont en dérivation : les conductances (inverse d'une résistance )s'ajoutent. G total = 1/ 10 + 1/15 + 1/17 = 0,2255 S soit R équivalent = 1/0,2255 = 4,43W. intensité I = (E-E') / (Réquivalent + r) = 4/ 17,43 = 229 mA. rendement h = U/E d'où E = U/h = 5,4 / 0,85 = 6,4 V.

mobile autoporteur Un mobile autoporteur S de masse m=452 g est abandoné sans vitesse initiale sur une table inclinée d'un angle a par rapport à l'horizontale. A l'instant choisi comme origine des dates, son centre d'inertie G se situe en A. On étudiera le mouvement du centre d'inertie G dans le reère (A, x, y)Ax horizontal à droite, Ay vertical vers le bas. Le mouvement de S se fait suivant la ligne de plus grande pente du plan incliné. Le solide S est soumis sur la table à une force de frottement unique, s'opposant au mouvement et d'intensité f inconnue. Le solide quitte la table en B, il n'est plus soumis qu'à l'action de la pesanteur. Le point B se situe à une hauteur h= 90 cm au dessus du sol. On négligera l'action de l'air sur S. Un dispositif informatisé permet d'enregistrer les coordonnées du centre d'inertie sur le plan incliné. temps (ns) x(cm) y (cm) 0 0 0 0,1 1,08 0,55 0,2 4,3 2,19 0,3 9,68 4,93 0,4 17,21 8,77 0,5 26,88 13,7 0,6 38,71 19,72 0,7 52,69 26,85 0,8 68,82 35,07 0,9 87,10 77,38 1 107,53 54,79 Déterminer la valeur de l'angle a (en degré) d'inclinaison de la table.( arrondir à l'entier le plus proche et utiliser cette valeur par la suite). Calculer la valeur de la force de frottement s'appliquant sur le mobile. La valeur de la vitesse en B est vB=2,69 m/s. Quelle est la longueur de la table en m ? Le solide quitte la table avec la vitesse vB précédente. Déterminer les coordonnées du point C de contact avec le sol. Calculer la durée du mouvement entre le point A et le point C.   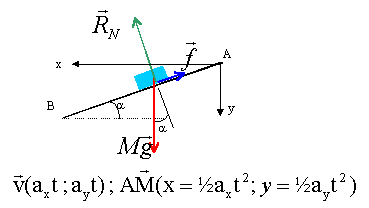corrigé le tableau de mesures permet le calcul de ax et ay : ax = 2x/t² = 2*1,08 10-2 / 10-2 = 2,16 m/s² ay = 2y/t² = 2*5,5 10-3 / 10-2 = 1,1 m/s² accélération a = racine carrée ( ax²+ ay²) = (2,16²+1,1²)½ = 2,42 m/s. tan a = ay / ax = 1,1 / 2,16 = 0,509 soit a = 27°. la 2ème loi de Newton projetée sur un axe parallèle au plan incliné, dirigé vers le bas, s'écrit : -f + mgsin a = ma soit f = m(gsin a- a)= 0,452(9,8 sin27 - 2,42) = 0,92N. th de l'énergie cinétique entre A et B : ½mv²B-0 = mg AB sina -f AB = AB(mg sina -f ) AB = ½mv²B/ (mg sina -f ) = v²B/(2a) = 2,69² / (2*2,42) = 1,5 m. chute libre : ( repère d'étude B, x, y) accélération ( 0, g); vitesse initiale( vB cosa ; vB sina) ; position intiale (0 ; 0) vitesse, primitive de l'accélération : (vB cosa ; gt+vB sina) position , primitive dela vitesse : (x= vB cosa t ;y = ½ gt²+vB sina t) trajectoire : y = ½ g x² / (vB cosa )² + x tana. y = 4,9 x²/ (2,69 cos 27)² + x tan27 ; y = 0,853 x² + 0,509 x au sol y = h= 0,9 m 0,9 = 0,853 xC² + 0,509 xC résoudre : xC = 0,76 m dans le repère (B, x, y) soit dans le repère (A, x, y) : xC = 0,76 +AB cos a = 2,1 m. durée du mouvement : entre A et b : Ab = ½at² soit t² = 2AB/ a = 3,2,42 = 1,24 et t = 1,113 s. entre B et C : t = xC/(vB cosa ) = 0,76 / (2,69 cos27) = 0,317 s total : 1,43s.

acide base   L'hélianthine est un indicateur coloré qui met en jeu un couple acide/base du type HIn/In- de pKa = 3,8 à 25°C. La zone de virage de l'hélianthine est [3,1 - 4,5]. La forme acide est rouge, la forme base conjuguée est jaune. Parmi les affirmations suivantes combien y en a t-il d'exactes ? - Une solution aqueuse d'hélianthine de pH=5,8 est jaune. - L'hélianthine peut être utilisé lors du titrage d'une solution d'acide éthanoïque par une solution d'hydroxyde de sodium. - L'hélianthine apparaît jaune en présence d'une solution d'acide chlorhydrique obtenue par la mise en solution de 10 mL de chlorure d'hydrogène dans 250 mL d'eau pure ( volume molaire = 24 L/mol) rappel : HCl + H2O--> H3O+ + Cl-. - Une solution aqueuse d'hélianthine telle que 3[HIn]=[In-] a un pH de 3,8. On dispose d'une solution d'acide chlorhydrique commerciale . Sur l'étiquette on li : densité = 1,19 ; pourcentage massique en chlorure d'hydrogène 36% ; masse molaire HCl : 36,5 g/mol. - Quel volume ( en mL) de la solution commerciale doit-on prélever pour préparer 3L de solution d'acide chlorhydrique à 0,02 mol/L 5 ; 26 ; 65 ; 85 ; 96 ; 112.  On fait réagir 10 mL d'acide sulfurique sur de la poudre d'aluminium. Il se forme 240 mL de dihydrogène. Les couples mis en jeu sont : H+ / H2 et Al3+ / Al. Le volume molaire vaut : 24 L/mol. - Déterminer la masse (mg) d'aluminium ayant réagi. 2 ; 30 ; 75 ; 120 ; 158 ; 180. On réalise le titrage de 20 mL d'une solution de dioxyde de soufre par une solution de diiode à 0,08 mol/L. Il faut verser un volume de 14,2 mL de diiode pour obtenir l'équivalence. Les couples mis en jeu sont : SO42- / SO2 et I2 / I-. Volume molaire = 24 L/mol. - Déterminer le volume en mL de dioxyde de soufre que l'on a dissout dans 500 mL d'eau pour obtenir la solution précédente. 148 ; 245 ; 432 ; 542 ; 682 ; 726. On verse 14,2 g d'acide propanoïque et 8,1 g de 3-méthylpentan-1-ol dans un ballon. On ajoute 2 mL d'acide sulfurique concentré et quelques grains de pierre ponce. On effectue un chauffage à reflux pendant 50 min. On détermine par un titrage approprié qu'il s'est formé 4,8 g d'ester. Parmi les propositions suivantes combien y en a-t-il d'exactes ? - La pierre ponce permet de réguler l'ébullition lors du chauffage à reflux. - L'acide sulfurique permet d'augmenter le rendement lors de la synthèse de l'ester. - L'acide propanoïque a été introduit en excès par rapport à l'alcool. - La formule semi-développée de l'ester s'écrit : CH3-CH2-CH2-COO -CH2-CH2-CH(CH3)-CH2-CH3. corrigé * à pH supérieur à pKa+1 la forme In- prédomine, donc couleur jaune. * CH3-COOH+HO- -->CH3-COO-+H2O à l'équivalence du dosage la base conjuguée CH3-COO- est majoritaire, donc le pHéqui est supérieur à 7. Or la zone de virage de l'indicateur coloré doit contenir le pHéqui. *0,01 / 24 = 4,16 10-4 mol HCl ; [H3O+]=4,16 10-4 /0,25 = 1,66 10-3 mol/L pH = -log1,66 10-3 = 2,78. donc l'hélianthine est rouge. *pH= pKa + log([In-]/[InH]) log([In-]/[InH]) = pH-pKa = -0,7 et [In-]/[InH] = 10-0,7 = 0,2 ; [InH] / [In-] = 5. * à pH = pKa alors [In-]=[InH] 1190 *0,36 / 36,5 = 11,74 mol/L pour la solution du commerce. Qté de matière : 3*0,02 = 0,06 mol 0,06 = 11,74 V soit V = 5,1 10-3 L = 5,1 mL. Al + 3H+ --> Al3+ + 1,5 H2(gaz) initial m / 27 mol n 0 0 en cours m / 27-x n-3x x 1,5x fin m / 27-xfin n-3xfin xfin 1,5xfin 1,5xfin = 0,24 / 24 = 0,01 mol d'où : xfin = 0,01/1,5 = 6,67 10-3 mol masse d'aluminium : 6,67 10-3 *27 = 0,18 g = 180 mg. SO2 + 2H2O=SO42- + 4H+ + 2e- oxydation I2 + 2e- = 2I- réduction SO2 + 2H2O + I2 = SO42- +4H+ + 2I- oxydo-réduction SO2 I2 ajouté initial n 0 en cours n-x x à l'équivalence n-xéqui=0 xéqui = 0,08*14,2 10-3 = 1,136 10-3 mol d'où n = 1,136 10-3 mol dans 20 mL de solution de SO2. soit 2,84 10-2 mol dans 500 mL volume de gaz SO2 dissous : 2,84 10-2* volume molaire = 2,84 10-2 *24 = 0,682 L=682 mL. * la pierre ponce régularise l'ébullition * l'acide sulfurique est un catalyseur : il augmente à la fois la vitesse d'estérification et celle d'hydrolyse de l'ester. Le catalyseur n'augmente pas le rendement, on atteint plus rapidement l'équilibre. * masse molaire : acide propanoïque CH3-CH2-COOH : 74 g/mol alcool : CH3-CH2-CH(CH3)-CH2-CH2OH ( C6H14O) : 102 g/mol ester CH3-CH2-COO-CH2-CH2-CH(CH3)-CH2-CH3 : 158 g/mol Qté de matière : acide :14,2/74 = 0,192 mol alcool : 8,1 / 102 =0,08 mol ( en défaut) donc x max = 0,08 mol ester : 0,08 * 158 = 12,64 g valeur théorique rendement h = 4,8 / 12,64 = 0,38 (38%)

pile   Une pile d'oxydo-réduction est constituée en associant les deux demi-piles suivantes : - Une lame de zinc de 7,34 g trempant dans 100 mL d'une solution de sulfate de zinc à 0,1 mol/L. - Une lame d'aluminium de 4,37 g trempant dans 100 mL d'une solution de sulfate d'aluminium à 0,1 mol/L Les deux demi-piles sont reliées par un pont salin contenant une solution gélifiée de chlorure de potassium. La pile débite un courant d'intensité I pendant 3 heures. On constate alors que la masse de l'électrode de zinc a diminué de 1,6 %. N=6,02 1023 mol-1 ; e= 1,6 10-19 C; Zn = 65,4 ; Al = 27 g/mol. Indiquer le schéma conventionnel de cette pile. Déterminer la valeur (mA) du courant débité par cette pile. Calculer les concentrations molaires ( mmol/L) des ions Al3+ et Zn2+. corrigé le zinc s'oxyde et libère des électrons : le zinc constitue la borne négative. Zn --> Zn2+ + 2e- anode négative. Al3+ + 3e- --> Al réduction donc cathode schéma conventionnel : - Zn / Zn2+ / / Al3+ / Al +. 3 Zn + 2 Al3+ --> 3 Zn2+ + 2Al initial 7,34 / 65,4 = 0,1122 mol 0,02 mol 0,1*0,1 = 0,01 mol excès en cours 0,1122-3x 0,02-2x 0,01+3x à t = 3 heures 0,1122 -1,8 10-3 donc 3 x = 1,8 10-3 mol x = 6 10-4 mol 0,02- 2*6 10-4 = 1,88 10-2 mol 0,01 + 3*6 10-4 = 1,18 10-2 mol Al2(SO4)3 --> 2Al3+ + 3SO42- donc 0,2*0,1 = 0,02 mol Al3+. à t = 3h, la masse de zinc diminue de 7,34 *1,6/100 = 0,11744 g soit 0,11744 / 65,4 = 1,8 10-3 mol [ Al3+] = 1,88 10-2 / 0,1 = 0,188 mol/L. [Zn2+]=1,18 10-2 /0,1 = 0,118 mol/L. Qté de matière d'électrons = 2* Qté de matière de zinc ayant disparu) (Zn --> Zn2+ + 2e- ) 2*1,8 10-3 = 3,6 10-3 mol d'électrons. Qté d'électricité : Q= 96500 * 3,6 10-3= 347,4 coulombs or Q(C) =I (A) t (s) d'où I = Q/t = 347,4 / (3*3600) = 0,032A = 32 mA.

saponification Dans un ballon on traite à chaud pendant deux heures, une masse m= 4g d'un triglycéride par un volume vB= 60 mL d'une solution de soude ( hydroxyde de sodium) de concentration cB=1 mol/L. On considére cette réaction comme totale. R-COO-CH2 - CH(OOC-R)- CH2-OOC-R (triglycéride)+ 3(Na+ + HO-) -->3(R-COO- + Na+) + CH2OH-CH(OH)-CH2OH ( glycérol). On refroidit l'ensemble et on procède au titrage de la quantité d'hydroxyde de sodium restante dans le ballon. Il faut verser un volume vA= 40,5 mL d'une solution d'acide chlorhydrique de concentration cA= 0,5 mol/L pour obtenir l'équivalence. Déterminer la masse molaire du triglycéride. Ce triglycéride est un triester du glycérol et d'un acide carboxylique saturé. Donner la formule brute de cet acide carboxylique. En réalité la réaction de saponification se fait avec un rendement de 85%. Calculer la masse (en kg) de glycérol obtenu lors de la saponification de 1,4 tonnes de ce triglycéride. C=12 ; O=16 ; H=1 g/mol. corrigé Qté de matière de soude: initiale : 0,06 mol restante : 0,5 * 40,5 10-3 = 0,02 mol donc 0,06-0,02 = 0,04 mol de soude a réagi avec0,04 / 3 = 0,01325 mol de triglycéride M, masse molaire du triglycéride : 0,01325 = 4 /M soit M = 4/0,01325 = 302 g/mol. R-COO-CH2 - CH(OOC-R)- CH2-OOC-R s'écrit : C6H5O6R3. 302 = 6*12 +5 +6*16 +3X d'où X= 43 g/mol R est identifié à C3H7. La formule brute de l'acide est C4H8O2. acide butanoïque CH3-CH2-CH2-COOH autre possibilité : acide 2-méthylpropanoïque : (CH3)2CH-COOH masse molaire : glycérol : 92 g/mol ; triglycéride : C15 H26 O6 : 302 g/mol Qté de matière de triglycéride : 1,4 106 / 302 = 4,63 103 mol donc 4,63 103 mol glycérol ( si rendement de 100%) soit en masse : 4,63 103 *92 = 4,27 105 g = 0,427 tonne. en tenant compte du rendement : 0,427*0,85 = 0,36 tonne. retour - menu