concours kiné C.E.E.R.R.F 03 physique 1 h - 40 points- chimie ½ h- 20 points. sans calculatrice.

mongolfière On néglige les frottements ; g=10m/s² A- Une mongolfière se déplace verticalement dans l'air. La masse de l'ensemble {aérostier, mongolfière} a une masse initiale m1 et un volume V supposé constant. Donner la direction, le sens et l'expression de la valeur de la poussée d'Archimède F. Le mouvement de la mongolfière est decendant et accéléré ; on note a la valeur de l'acélération de l'ensemble ( a<g). Appliquer dans le référentiel terrestre supposé galiléen la seconde loi de Newton au système et projeter la relation obtenue sur un axe vertical orienté vers le bas. L'aérostier lâche du lest. Le mouvement de la mongolfière est maintenant accéléré vers le haut avec une accélération de même valeur a. La masse de l'ensemble est maintenant m2. -Appliquer dans le référentiel terrestre supposé galiléen la seconde loi de Newton au système et projeter la relation obtenue sur un axe vertical orienté vers le haut. En déduire en fonction de a, g, m1, l'expression de la masse m du lest jeté par dessus bord. B- Du lest est lâché sans vitesse initiale à un instant t=0, lorsque la mongolfière est immobile à l'altitude h=320 m. Etablir l'équation horaire z(t) du mouvement de chute du centre d'inertie G du lest. L'axe zz' est orienté vers le haut et son origine est au niveau du sol. Exprimer puis calculer l'instant t de l'impact au sol. C- De retour - menu au sol l'aérostier passe un examen médical nécessitant l'ingestion d'une dose d'iode 131 de masse m0=0,8 m g. La demi-vie de cet isotope radioactif émettant des rayons b - est t½=8 jours. Z 51 52 53 54 élément Sb Te I Xe donnée : ln10/ln2 = 3,3 Ecrire l'équation de désintégration de l'iode 131 Déterminer la masse de cette substance radioactive encore présente dans l'organisme 32 jours après l'ingestion. Au bout de combien de jours après l'ingestion, la masse m de cette substance restante est inférieure à 1% de la masse m0 initialement ingérée ? corrigé poussée : verticale, vers le haut, valeur = poids du volume d'air déplacé = rair Vg poids: vertical, vers le bas, valeur =mg Ecrire la 2ème loi de Newton sur un axe vertical vers le bas ( descente) : m1g - rair Vg = m1a. (1) a= g(1 - rair Vg/m1) Ecrire la 2ème loi de Newton sur un axe vertical vers le haut ( montée) : -m2g + rair Vg = m2a. (2) a = g( rair Vg/m2-1) masse du lest jeté : m= m1-m2 (3) ; (2) donne : m2 = rair Vg /(a+g) repport dans (3) : m= m1- rair Vg /(a+g) (1) donne : rair Vg = m1(g-a) (3) s'écrit : m= m1-m1(g-a) /(g+a) = 2am1/(a+g). mouvement de chute libre verticale, sans vitesse initiale. axe zz' orienté vers le haut, sens contraire du vecteur accélération vitesse primitive de l'accélération v = -gt position, primitive de la vitesse z = -½gt² +h. au sol z=0 d'où t² = 2h/g = 2*320/10 = 64 ; t= 8s. 13153I-->AZX+0-1e conservation du nombre de nucléons : 131=A+0 conservation de la charge : 53 = Z-1 d'où Z=54 et en conséquence X est le xénon Xe 32 jours correspond à 4 périodes : la masse initiale est divisée par 16 = 24. 0,8 10-6/ 16 = 80 10-8 /16 = 5 10-8 g. masse finale m <= masse initiale m0 /100 m=m0 e-lt soit ln (m0 /m)=lt avec l=ln2/T ( T demi-vie ou période en jours) ln ( m0 /m)= t/T ln2 ; ln 100 = t/T ln 2 ; 2 ln 10 = t/T ln2 t/T = 2ln10/ln2 = 6,6 soit t = 6,6 T =6,6*8 = 52,8jours au delà de 52,8 jours la masse initiale est divisée par 100.

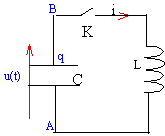
dipôle LC La résistance de la bobine est négligeable. La tension aux bornes du condensateur vaut U0=10 V, l'interrupteur K étant ouvert. A l'instant t=0 on ferme l'interrupteur K. Nommer le phénomène obtenu. Des enregistrements ont permis d'obtenir l'expression de u(t) et i(t) : u(t)=10 cos(2 104t) en volt ; i(t) = 20 sin ()2 104t en mA. - Ecrire la relation entre u, C et du/dt. Justifier. - Montrer que C= 100 nF. - Calculer la valeur de L. - Calculer la valeur de l'énergie E du circuit. - Comment varie E au cours du temps ? - Calculer la période propre T0. On appelle t1 la date à laquelle, pour la première fois après la fermeture de K, l'énergie est répartie de façon égale entre la bobine et le condensateur. Calculer u(t1) et i(t1). Données : rac carrée (2) =1,4 ; rac carrée (50) = 7,1.   corrigé oscillations libres non amorties : régime sinusoïdale q= Cu(t) ; i = - dq/dt = -Cdu/dt ( signe - car décharge ) ; di/dt = -Cd²u/dt² = -Cu" Ldi/dt = u(t) soit L(-Cd²u/dt² )= u ou bien LCu"+u=0. u=10 cos(2 104t) du/dt = u' = 10*2 104 (-1) sin(2 104t) or i = - dq/dt = -Cdu/dt = -C(-1) 2 105sin(2 104t) = 2C 105sin(2 104t) or i= 20 10-3sin(2 104t) ampères d'où 20 10-3 = 2C 105 soit C= 10-7F = 100 nF. w0=2 104 rad/s ; w02 = 1/(LC) soit LC = 1/(4 108) L= 1/(4 108* 10-7) = 1/40 H= 1000/40 mH=25 mH. à t=0 , condensateur chargé, i=0 le condensateur stocke l'énergie du dipôle LC E=½CU0²= 0,5 10-7 10² = 50 10-7 = 5 10-6 = 5mJ. si la résistance du circuit est nulle, il n'y a a pas d'amortissement et l'énergie reste constante. période T0=2p/w0=6,28 / 2 104 = 3,14 10-4 s = 0,314 ms. le condensateur stocke la moitié de l'énergie du dipôle LC soit 2,5 10-6 J 2,5 10-6 =½Cu²(t1) = ½10-7 10² cos²(2 104t1) 2,5 10-6 =5 10-6 cos²(2 104t1) 0,5 = cos²(2 104t1)soit rac carrée (0,5) =0,707 = cos(2 104t1) 0,707 = cos (0,785) , angle en radian. 0,785=2 104 t1 ; t1= 3,925 10-5 s = 0,0392 ms . soit 1/8 période. u(t1)=u=10 cos(2 104t1) = 10 cos (2 104*3,925 10-5) = 7,07 V. i(t1)=20 10-3sin(2 104t1) = 20 10-3 sin (2 104*3,925 10-5) = 14,2 10-3 A.

lunette astronomique Une lunette astronomique utilisée pour observer la lune est constituée d'un objectif de distance focale f'1 = 100 cm et d'un oculaire de distance focale f'2 = 2 cm, assimilable à des lentilles minces convergentes. La lunette est afocale, les centres optiques des deux lentilles sont distants de 102 cm. La lune étant considérée à l'infini a un diamètre apparent a=9,3 10-3 rad. L'objectif en donne une première image AB, A étant sur l'axe du montage - Où est située cette image. Justifier. - Quelle est sa grandeur ? Où est située l'image finale ? Justifier sans figure. - Quel est l'interêt du montage afocal ? L'utilisateur veut projeter sur une plaque photographique une image A'B' de la lune 4 fois plus grande que l'image AB précédente. Dans quel sens dioit-il déplacer l'oculaire ? Justifier - Calculer le déplacement de l'oculaire. - Où doit-il placer la plaque photographique ? Donnée : tan a = a (rad) corrigé Objet ( la lune) à l'infini, donc l'image donnée par l'objectif se trouve dans le plan focal image de cette lentille. La grandeur de l'image est proche de : AB = f1 a = 1*9,3 10-3 = 9,3 10-3 m La lunette étant afocale, l'image définitive A1B1 se trouve à l'infini et en conséquence l'image intermédiaire se trouve dans le plan focal objet de l'oculaire. L'oeil n'accomode pas et observe l'image sans fatigue. On doit obtenir une image réelle A2B2 sur la plaque photographique ; l'objet AB (image intermédiaire) ne doit pas se trouver entre le centre optique de l'oculaire O2 et le foyer principal objet de l'oculaire ( sinon l'image sera virtuelle) : il faut donc déplacer l'objectif vers la droite, dans le sens de la lumière. ( ce qui est écrit en gras et en bleu est une grandeur algèbrique) |grandissement| = |O2A2 /O2A | = 4 soit O2A2 = 4 |O2A | O2A2 positif et O2A négatif donc O2A2 = -4O2A formule de conjugaison :1/f2 = 1/O2A2 -1/O2A. 1/f2 = 1/(-4O2A) -1/O2A= -1,25 /O2A O2A = -1,25 2= -1,25*0,02 = 2,5 10-2 m soit un déplacement de 5 mm vers la droite. La plaque photo se trouve à droite de l'oculaire ( dans le sens de la lumière gauche vers la droite) O2A2 = 4 |O2A | = 4*2,5 10-2 = 0,1 m.

ammoniac Le pH d'une solution aqueuse S0 d'ammoniacNH3 de concentration apportée c0=0,01 mol/L vaut 10,6 à 25°C. Ecrire l'équation de la réaction de l'ammoniac avec l'eau. Exprimer puis calculer le quptient de réaction à l'état d'équilibre Qr,éq et le taux d'avancement final t0. A partir du système à l'équilibre on envisage différentes situations : - On ajoute une pointe de spatule de chlorure d'ammonium solide. - On ajoute une goutte d'une solution diluée d'acide chlorhydrique ( sans variation de volume) - On chauffe la solution ( la solubilité du gaz évolue en sens inverse de la température) Préciser le sens d'évolution du système dans les trois situations. On dilue 10 fois la solution S0 précédente et on mesure le pH de la solution diluée notée S1 : pH=10.Calculer le taux d'avancement final t1 de la réaction dans cette nouvelle solution. - Comparer t0 à t1 et conclure.  Données : 10-0,4 = 0,4 ; 1/6 = 0,17. corrigé NH3 + H2O = NH4+ + HO- ; Qr,éq = [NH4+ ]éq[HO-]éq / [NH3]éq avec [NH4+ ]éq=HO-]éq = 10-14 /10-pH = 10-3,4 = 10-3*10-0,4= 4 10-4 mol/L [NH3]éq proche de C0, l'ammoniac étant peu dissociée. Qr,éq =(4 10-4)² / C0 = 16 10-8 / 10-2 = 1,6 10-5. taux d'avancement final t1= xéq / x max = 410-4 / 10-2 = 0,04. ajout NH4+ : équilibre déplacé vers la gauche ; sens indirect ; consommation de l'ion ammonium ajouté. ajout ion oxonium H3O+ : réaction acide base H3O+ + HO- --> 2H2O, l'ion HO- disparaît équilibre déplacé vers la droite ; sens direct ; formation d'ion hydroxyde. on chauffe la solution : l'ammoniac est moins soluble ( disparition de NH3 au profit de l'ion NH4+ équilibre déplacé vers la droite ; sens direct ; formation d'ion NH4+. facteur de dilution : xmax = 10-3 mol taux d'avancement final t0= xéq / x max = 10-4 / 10-3 = 0,1. ajout d'eau : l'équilibre est déplacé vers la droite, consommation de l'eau ajoutée; sens direct.

L'eaux de chaux   L'eau de chaux est une solution saturée d'hydroxyde de calcium Ca (OH)2 dont la solubilité à 25°C est s=0,01 mol/L. - Ecrire l'équation de la mise en solution de l'hydroxyde de calcium. - Donner l'expression de la constante d'équilibre K1 associée à cette équation. - Exprimer K1 en fonction de s. - Calculer K1. On fait barboter dans 1 L d'eau de chaux un courant de dioxyde de carbone. - Deux réactions acido-basiques successives se produisent dans la solution. Ecrire leurs équations. - La constante d'équilibre associée à la mise en solution du carbonate de calcium CaCO3 solide a pour valeur à 25°C K2 = 4 10-9. Ecrire l'équation de cette réaction et donner l'expression de K2. - Quelle quantité minimale de dioxyde de carbone faut-il dissoudre dans la solution étudiée pour observer un début de précipitation de carbonate de calcium ? - Justifier l'utilisation de l'eau de chaux pour détecter la présence de dioxyde de carbone. corrigé Ca (OH)2 = Ca2+ + 2HO- (1) K1=[Ca2+] [HO-]² solution électriquement neutre : 2[Ca2+]=[HO-] = 2s K1=s *(2s)² = 4 s3= 4 10-6. HO- + CO2 = HCO3-. 2HO- + CO2 = CO32- + H2O (3) K3=[CO32- ] /([CO2][HO-]²) CaCO3= Ca2+ + CO32- ; K2 = [Ca2+] [CO32- ]= 4 10-9. le carbonate de calcium commence à précipiter dès que le produit [Ca2+] [CO32- ] atteint la valeur 4 10-9. dans l'eau de chaux saturée : [Ca2+]= 0,01 mol/L cette valeur reste inchangée lors de l'ajout de CO2. 0,01[CO32- ]= 4 10-9. [CO32- ] = 4 10-7 mol/L 2HO- + CO2 = CO32- + H2O (3) donne [CO32- ] = [CO2]= 4 10-7 mol/L Une quantité très faible de CO2 dissout peut être détectée. retour - menu