|
|
|
|
|
|
- L'air est un mélange de gaz. Entourer les gaz
dont la fraction molaire dans l'air est supérieur
à 10 %.
Ar ; CO ; CO2 ; H2 ; H2O ; O2 ; NO2 ; N2 - Soit un bateau naviguant à une vitesse
constante de 5 m.s-1 sans vent. Un singe est
monté sur le mat, à 7 mètres
au-dessus du pont. Il laisse tomber une noix de coco.
Où tombe cette noix ? On négligera les
frottements de l'air.
- Quelle est la vitesse de translation moyenne de la Terre sur son orbite autour du Soleil ?
- Quelle puissance électrique faut-il pour chauffer de 20°C à 60°C les 200 litres d'eau contenus dans un chauffe-eau en une durée de 5 h ? On considèrera ce chauffe-eau convenablement isolé thermiquement.
- Citez quatre formes d'énergie dites renouvelables pouvant être utilisées pour produire de l'électricité.
O2 et N2.
au pied du mât tant que le mouvement est rectiligne et uniforme
hydroélectricité ; solaire, géothermie; éolien ; biomasse ( bois, colza..)
distance Terre Soleil D=1,5 1011 m ; période : T =365*24*3600 = 3,15 107 s
en supposant l'orbite circulaire :
2pD = v T soit v = 2pD / T = 6,28*1,5 1011 / 3,15 107 = 30 km/s.
capacité thermique massique de l'eau : c = 4180 J kg-1 K-1.
Q = mc Dq= 200/4180*(60-20)=3,34 107 J.
Puissance (W) = énergie (J) / durée (s) = 3,34 107 / (5*3600) = 1,85 kW.
- Questions préliminaires :
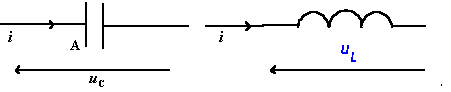
- La capacité du condensateur vaut C, l'armature A porte la charge q. Donner les relations entre : q et i, q et uC, i et uC.
- La bobine est idéale (r = 0), son inductance vaut L. Donner la relation entre i et uL. - On considère le montage suivant :
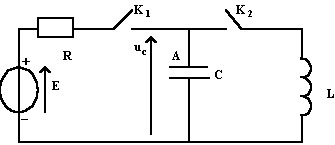
Initialement, K1 et K2 sont ouverts. Le condensateur est déchargé. R1 = 1 kW ; C= 10mF ; L=1H ; E=10 V
- On ferme l'interrupteur K1 à t = 0 et K2 reste ouvert, le condensateur se charge à travers R. Donner l'équation différentielle vérifiée par uC(t).
- Quelle est l'expression littérale de la constante de temps t ?
- Donner la solution littérale de l'équation différentielle précédente. - A l'instant t1=10 ms on ouvre
K1 et on ferme K2 de façon
simultanée.On note q la charge portée par
l'armature A.
- Donner la valeur numérique, notée U0 de uC(t) à l'instant t1.
- A partir de l'instant t1, donner l'équation différentielle vérifiée par q (t), puis la nouvelle équation différentielle vérifiée par uC(t).
- Quelle est la valeur numérique de la période T0 des oscillations.
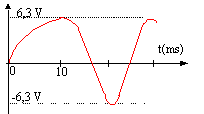
- De façon très schématique, esquisser l'allure de la tension uC(t) depuis l'instant t0.corrigé
i = dq/dt = q' ( dérivée de la charge par rapport au temps)
E= Ri + uC ; E=RCu'C + uC ; u'C + 1/(RC) uC = E/(RC)
solution de cette équation différentielle : uC = E(1-e-t/t)
U0 = E(1-e-1) = 0,63 E = 6,3 V.
décharge du condensateur à travrs la bobine : uC = L di/dt avec i = -dq/dt = -CduC /dt = -Cu'C ; i' = -Cu"C ;
uC = L(-Cu"C ) soit u"C + 1/(LC)uC =0
w0² = 1/(LC) = 1/(10-5) = 105 soit w0= 316,2 rad/s.
T0 = 2p/w0= 2*3,14 / 316,2 = 0,02 s = 20 ms.
En
effectuant des fouilles, on a découvert une momie.
Pour déterminer la date approximative de sa mort, on
utilise la méthode de datation au carbone 14. Cet
isotope du carbone est constamment produit lors du
bombardement de l'azote atmosphérique par les
neutrons cosmiques. Le carbone 14, assimilé par les
organismes vivants, se trouve donc présent en
très faible quantité dans ces organismes.
L'expérience montre que la proportion R des deux
isotopes et est la même dans l'atmosphère et
dans les organismes vivants : 1 atome de 14C pour
106 atomes de 12C. Après la
mort, la proportion de 14C diminue car il est
radioactif b-,
de demi vie t½ = 5570 ans.
- Ecrire l'équation de désintégration du 14C et donner le nom des produits de la réaction.
- Dans un
prélèvement de m = 100 mg de
matières organiques sur la momie, on constate
qu'il y a r=10%
en masse de carbone. Cet échantillon
présente une activité de 1 180 Bq. Calculer
la constante radioactive l.
- Evaluer le nombre N0 d'atomes de 14C contenus dans l'échantillon lors de l'ensevelissement (la masse de 14C est négligeable devant la masse totale de carbone).
- Quelle était l'activité A0 de l'échantillon au moment de la mort.
- En déduire l'âge approximatif t de la momie.
masse molaire : C = 12 g/mol. constante d'Avogadro : NA=6 1023.
deuxième ligne du tableau périodique : Li, Be, B, C, N, F, Ne.
146C --> AZX + -10e
conservation du nombre de nucléons : A+0 = 14
conservation de la charge : 6=Z-1 soit Z= 7 ( élément azote N)
l= ln2 / t½ =0,693 / 5570 = 1,244 10-4 an-1 ou 0,693 / (5570*365*24*3600) = 3,94 10-12 s-1.
masse de carbone 0,01 g ; 0,01 / 12 = 8,333 10-4 mol de carbone
nombre de noyaux : 8,333 10-4 * 6 1023 = 5 1020 noyaux
N0 = 5 1020 / 106 = 5 1014 noyaux 14C au moment de l'ensevelissement
activité A0 = lN0 =3,94 10-12 *5 1014 =1970 Bq.
A = A0 e-lt ; ln (A0/A) =l t soit t =1/l ln (A0/A) = 1/1,244 10-4 * ln(1790/1180)= 3350 ans.
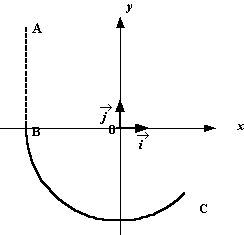
A(-R ; h) ; B(-R ; 0) ; C(0,7 R ; -0,7 R)
Un point matériel M de masse m, soumis au champ uniforme de la pesanteur est lâché sans vitesse initiale en A. De B à C, il se déplace sans frottement sur un arc de cercle de rayon R et de centre O . La trajectoire reste dans le plan du cercle (O, x, y). Au-delà du point C, il est à nouveau uniquement soumis à son propre poids. On exprimera les résultats littéraux en fonction de g, R et h .
- Déterminer la vitesse absolue vB du point M en B.
- Déterminer la norme vC, puis la vitesse absolue du point M en C.
- Déterminer les coordonnées x et y du point M au-delà de C en fonction du temps. (On prendra comme origine des temps l'instant où le point M est en C).
- En déduire l'équation cartésienne de cette trajectoire.
- Déterminer la cote y maximale de cette trajectoire (en utilisant de préférence, le théorème de l'énergie).
théorème de l'énergie cinétique ( seul le poids travaille)
entre A et B : v²B = 2gh
entre A et C : ½mv²C-0 = mg( zA-zC) = mg(h-(-0,7 R)) = mg(h+0,7R) ; v²C=2g(h+0,7 R).
le vecteur vitesse est tangent à l'arc de cercle en C.
ce qui est écrit en gras et en bleu est un vecteur.
à l'instant initial : vC(0,7 vC ; 0,7 vC) ; OM0 ( 0,7 R ; -0,7 R)
chute libre a(0; -g)
la vitesse est une primitive de l'accélération : v(0,7 vC ;-gt+ 0,7 vC)
le vecteur position est une primitive du vecteur vitesse :
OM( x= 0,7 vC t +0,7R ; y = -½gt² + 0,7 vCt -0,7 R)
trajectoire : t = (x-0,7 R) / (0,7vC)
report dans y(t) : y = -½g (x-0,7 R)²/ (0,7vC)² + (x-0,7 R)-0,7 R.
altitude maxi ym : le vecteur vitesse est horizontal et sa composante verticale est nulle soit v = 0,7 vC ;
théorème de l'énergie cinétique entre A et altitude maxi: seul le poids travaille
½m( 0,7 vC)²-0 =mg(h-ym) ; vC² = g(h-ym)
or v²C=2g(h+0,7 R) d'où : g(h+0,7 R)/2 = g(h-ym) ;
(h+0,7 R)/2 = h-ym soit ym = ½(h -0,7R).
- On effectue dans un réacteur maintenu à
une température constante le mélange d'une
mole d'acide acétique (ou acide
éthanoïque) et d'une mole d'éthanol
à la date t = 0. La réaction chimique qui
s'ensuit, athermique, produit de l'eau et un produit
organique X :
- De quel type de réaction s'agit-il ?
- Ecrire l'équation-bilan de la réaction.
- Donner le nom du produit X ; calculer sa masse molaire. - Afin de suivre l'évolution chimique du système, on prélève au cours du temps des échantillons correspondant à 1/100ème en volume du mélange réactionnel, que l'on refroidit instantanément. L'acide acétique contenu dans chaque échantillon est alors dosé par une solution décimolaire (0,1 mol. L-1) de soude (hydroxyde de sodium). Le graphe suivant rend compte de l'évolution du système à partir des résultats expérimentaux.
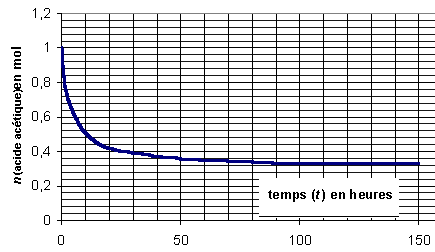
- Quel est le volume équivalent de soude
versé lors du dosage de l'acide de
l'échantillon à t = 50 h ?
- A partir de la courbe expérimentale donnant la
quantité d'acide acétique du mélange
réactionnel en fonction du temps, évaluer la
vitesse instantanée de la réaction à la
date t = 40 h.
- Déterminer le temps de demi-réaction.
- Calculer le rendement de la réaction à
l'équilibre.
- Pour augmenter le rendement, on peut :
Réaliser au départ un mélange non
équimolaire ; Augmenter la température ;
Distiller le produit X formé au cours de la
réaction ; Ajouter un catalyseur ; Ajouter de l'eau ;
Augmenter l'agitation du mélange.
- Sur le graphique du document réponse,
représenter l'allure de la courbe nacide
acétique = f (t) si on réalise
l'expérience en présence d'une faible
quantité d'acide sulfurique.
esterification: CH3-COOH + CH3-CH2OH=CH3-COO-CH2-CH3 + H2O
nom de l'ester : éthanoate d'éthyle ; masse molaire 88 g/mol.
à t = 50 heures, n AH= 0,36 mol soit 3,6 10-3 mol dans l'échantillon
à l'équivalence du dosage : n AH= Qté de matière de soude versée
3,6 10-3 = 0,1 v soit v = 3,6 10-2 L = 36 mL.
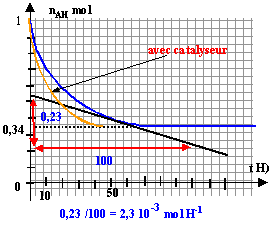
temps de demi-réaction t½ : temps au bout duquel l'avancement est égal à la moitié de l'avancement final
xfin =0,66 mol d'ester ; à t½ x = 0,33 mol d'ester soit nAH=0,67 mol. (lecture graphe t½ = 10 h)
rendement = Qté de matière d'ester obtenue / Qté de matière d'ester théoriquement possible = 0,66 / 1 = 0,66 ou 66%.
Pour augmenter le rendement, on peut :
-Réaliser au départ un mélange non équimolaire ;
- Distiller l'ester formé au cours de la réaction ;
On réalise un pendule simple non amorti avec une masse M (M = 500 g) accrochée à un fil de masse négligeable et de longueur L. La longueur du fil varie avec la température selon la loi L = L0(1+kq), q étant la température en degré Celcius, L0 la longueur à 0 °C et k le coefficient de dilatation k = 2.10-5 °C-1. On écarte le pendule de la position d'équilibre d'un angle a = 8 ° puis on lâche la masse sans vitesse initiale en un lieu où l'intensité de la pesanteur est g = 9,81 m/s². La période des petites oscillations de ce pendule simple est T = 2,0000 s lorsqu'il est conservé dans une enceinte à 20 °C.
- Calculer la longueur du fil L à 20
°C.
- Déterminer la vitesse v0 de la masse quand elle passe par sa position d'équilibre (a = 0 °). - La température de l'enceinte est à
présent de 0 ° C. Quelle est la
période T0 du pendule
précédent ?
- Une oscillation correspondant à une demi-période, combien d'oscillations effectuera-t-il en une journée (24 heures) ? - La température de l'enceinte est à
présent de q' ° C.
On note que la durée de 100 périodes T est
de 200,0200 s. Calculer la température
q' .
corrigé
période T = 2p(L/g)½ soit L = T² g / (4p²) = 9,81 / 3,14² = 0,99396 m (0,994 m)
v²0 = 2gL(1-cosa) = 2*9,81*0,994(1-cos8) = 0,19 ; v0 = 0,436 m/s.
période T0 = 2p(L0/g)½ avec L = L0(1+kq) soit L0 = L/(1+kq) = 0,994 /(1+2 10-5*20 ) =0,9936 m
T0 = 6,28(0,9936 / 9,81)½ = 1,9996 s.
nombre d'oscillations : 24*3600 / 0,9998 = 86415.
2,0002 = 2p(L/g)½ soit L =2,0002²*g / (4p²) = 0,9942 m
L = L0(1+kq') soit kq' = L/L0-1 = 0,9942 / 0,9936 -1 = 6,03 10-4.
q' =6,03 10-4/ 2 10-5 = 30°C.
On utilise le montage ci-dessous comportant une résistance R et un condensateur déchargé C.
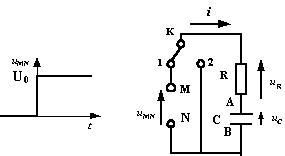
L'inverseur K étant en position 1, on applique entre les bornes M et N l'échelon de tension uMN dont l'évolution est représentée en fonction du temps t. Données : R = 2,7 kW ; C= 2,2 mF ; U0 = 12 V
- Choisir parmi les 5 courbes ci-dessous, celle qui
représente l'évolution en fonction du temps
t :
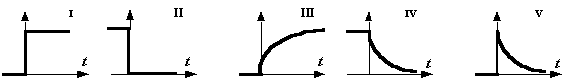
- de la tension uC aux bornes du condensateur ;
- de la tension uR aux bornes de la résistance ;
- du courant i dans le circuit. - Donner l'expression littérale et la valeur numérique de la constante de temps t de ce circuit.
- Déterminer en régime permanent la
valeur limite :
- qA de la charge de l'armature A du condensateur ;
- qB de la charge de l'armature B du condensateur ;
- EC de l'énergie emmagasinée par le condensateur. - L'inverseur K est maintenant amené en position
2. Donner alors l'équation différentielle
à laquelle obéit la tension uC
aux bornes du condensateur.
- Donner, en fonction de R, C et U0, l'expression et la valeur du coefficient directeur de la tangente à l'origine de cette courbe.
A l'instant initial ( fermeture de K) le condensateur n'est pas chargé uC=0 ; uC va ensuite croître donc courbe III
la tension uR aux bornes du résistor vaut : uMN-uC ; sa valeur initiale est uMN puis uR décroît jusqu'à s'annuler ; courbe V.
Aux bornes d'un résistor intensité et tension sont proportionnelles donc l'intensité correspond à la courbe V.
t=RC= 2700*2,2 10-6 = 5,94 ms.
qA : A relié à la borne positive du générateur lors de la charge, donc qA positive et qB= -qA négative
qA = CU0 = 2,2 10-6*12 = 2,64 10-5 coulomb.
énergie maximale stockée : ½CU²0 = 0,5 *2,2 10-6*12² = 1,584 10-4 J.
à la décharge l'intensité change de sens : -Ri + uC=0 avec i = -dqA/dt = -CduC/dt = -Cu'C
RCu'C+ uC=0 soit u'C+ 1/(RC) uC=0
solution du type uC= U0 e-t/(RC).
en dérivant : u'C= -U0 / (RC)e-t/(RC).
le coefficient directeur de la tangente à l'origine vaut : -U0 / (RC)= -12/( 5,94 10-3)= -2020 Vs-1.
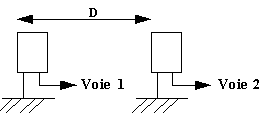
Un émetteur émet des ultrasons par salves. Deux récepteurs, disposés à deux endroits différents sur le trajet des ondes ultrasonores, permettent d'enregistrer les ultrasons émis et de les visualiser sur l'écran d'un oscilloscope. Le dispositif expérimental est schématisé ci-dessous.
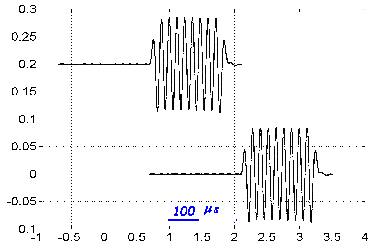
On observe à l'oscilloscope les signaux reproduits ci-dessous, la vitesse de balayage étant de 100 ms/div
- Exprimer la longueur d'onde l en fonction de la fréquence f et de la célérité c.
- Justifier cette relation par une équation aux dimensions.
- En utilisant l'un ou l'autre des signaux, déterminer la fréquence des ultrasons.
- En comparant les deux signaux captés par les deux récepteurs distant de D = 96 mm, calculer la célérité des ultrasons dans l'air.
- Cette onde véhicule-t-elle (plusieurs réponses sont possibles) ? une information ; de la matière ; de l'énergie.
- Une onde lumineuse véhicule t-elle (plusieurs réponses sont possibles) ? une information ; de la matière ; de l'énergie.
- Donner la valeur numérique correspondant à la fréquence basse des ultrasons.
- Préciser le sens d'évolution des grandeurs suivantes lorsque l'expérience est réalisée dans l'eau. fréquence ; longueur d'onde ; célérité.
l = c / f
f : fréquence (Hz ou s-1) ; c : célérité (m s-1 ) ; l longueur d'onde (m)
lecture graphe : 4 périodes sont représentées par 100 ms ; T= 25 m s = 2,5 10-5 s.
f = 1/ 2,5 10-5 = 40 000 Hz = 40 kHz.
retard du second signal sur le premier (lecture graphe) : 280 m s = 2,8 10-4 s
célérité : 96 10-3 / 2,8 10-4 =343 m/s.
Une onde véhicule une information, de l'énergie.
fréquence basse des ultra-sons : 20 kHz
dans l'eau : fréquence constante, caractèristique d'une onde.
la célérité est plus grande que dans l'air ; donc la longueur d'onde sera plus grande.