d'après concours kiné Lariboisière 03 sans calculatrice

radioactivité (8 points) Ce Q.C.M. comporte huit questions à quatre réponses chacune. Dans un échantillon radioactif de N noyaux instables le nombre de noyaux D N qui se désintègre pendant la durée Dt est a. DN = N0e-lt ; b. D N= -lNDt. ; c- D N= lNDt. ; d- D N= -NDt / l. La constante de désintégration radioactive l d'un nucléide a. s'exprime en s-1 b. vérifie l'égalité l.In 2 = t½ c. vérifie l'égalité l t½ =Ln2 d. vérifie l'égalité 2.t½ =l On dispose d'un échantillon de matière radioactive a. Au bout de une demi-vie, la moitié des atomes radioactifs s'est désintégrée b. Au bout d'une demi-vie, la masse de l'échantillon est égale à la moitié de la masse initiale. c. Au bout de deux demi-vies ,les trois quarts des atomes se sont désintégrés d. Au bout d'une demi-vie, il reste la moitié des atomes radioactifs initialement présents L'énergie de liaison d'un noyau atomique a. est l'énergie à fournir pour dissocier en ses constituants b. est une grandeur toujours négative c. peut s'exprimer en MeV ou en MeV /nucléon d. est récupérée par le milieu extérieur lors de la constitution du noyau. Au coeur du soleil se produit la réaction d'équation 21H + 21H ->42He où 21H est le deutérium. a. Cette équation est correctement écrite. b. Le deutérium est un élément différent de l'élément chimique hydrogène c. Il s'agit d'une réaction de désintégration nucléaire d. Les masses, en unité de masse atomique, sont respectivement 1,007276 u pour H , 2,013451 u pour le deutérium et 4,0015 pour 42He, l'énergie libérée par cette réaction vaut 4,4 MeV (1 u correspond à 931 MeV) En cas d'explosion du réacteur nucléaire d'une centrale, de l'iode 131 et du césium 137 peuvent se répandre dans l'atmosphère. On donne les numéros atomiques des éléments suivants : I: Z=53 ; Cs : Z = 55 a. Ces deux radionucléides possèdent respectivement 78 et 82 protons. b. l'iode est radioactif b- ceci signifie qu'il émet un proton c. L'iode 131 a une demi-vie de 8 jours ce qui signifie qu'il disparaît totalement en 16 jours d. On peut expliquer le phénomène b- qui s'est produit au coeur du noyau par le fait qu'un neutron s'est transformé en proton L'équation bilan de la transformation de l'iode et celle du césium sont : a. 131 53I --> 131 54Xe + 0-1e b. 131 55I --> 131 54Xe + 0+1e c. 137 55Cs --> 131 54Xe + 0-1e d. 137 53Cs --> 131 54Xe + 0+1e Dans la relation E =Dmc² a. D m représente la masse de la particule éjectée pendant la réaction nucléaire b. D m représente la masse de toutes les particules impliquées dans la réaction nucléaire c. Dm représente la perte de masse entre les noyaux pères et les noyaux fils. d. E représente l'énergie à fournir au noyau au repos pour le dissocier en nucléons isolés.   corrigé 1b- est la bonne réponse 2a- et 2c- sont exactes 3a- et 3 d- sont exactes 4 a- ; 4 c- et 4 d- sont exactes 5a- est exacte ; 5c : réaction de fusion 5d : défaut de masse |Dm |= 2*2,013451-4,0015 = 0,025 u énergie correspondante : E= 0,025*931 = 23,64 MeV 6a : nombre de protons = nombre de charge= Z; nombre de neutrons = A-Z. 6b: emision d'un électron. 6c : en 16 jours, soit deux périodes, il reste N0/2² = N0/4 noyaux initiaux d'iode 131 6d- est exacte. 7a- et 7d- sont exactes. 8c- et 8 d sont exactes

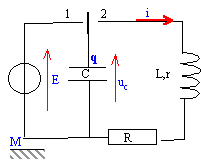
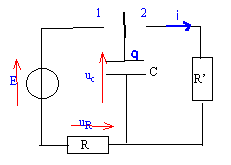
circuits RC, RL, RLC(12 points)   Les trois parties peuvent être traitées de façon indépendante. 1 ère partie On décide d'étudier la charge et la décharge d'un condensateur dans des résistances. On réalise le schéma de la figure 1. Seule est connue la valeur de R (R= l00 W). Les valeurs de la capacité C du condensateur et de la f.e.m E du générateur de tension parfait ( alimentation stabilisée) ne sont pas connues. On a placé une interface permettant l'étude de la tension uc(t) à l'ordinateur. Initialement , le condensateur n'est pas chargé. On place l'interrupteur en position 1 à t=0 en déclenchant l'acquisition Sur un schéma soigné indiquer les branchements de la masse et de la voie A à effectuer pour avoir uc(t) . 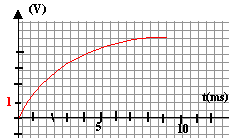En annexe (graphique 1 ) on a donné l'enregistrement correspondant à uc(t) A partir de cette courbe déterminer en justifiant les valeurs de la f.e.m E du générateur, la constante de temps t du circuit, la capacité C du condensateur, la valeur I0 de l'intensité du courant circulant dans le circuit à la date t=0 Le condensateur étant chargé, on bascule rapidement l'interrupteur en position 2. On obtient le graphique 2 de l'annexe. 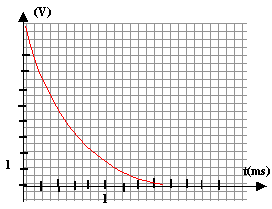a. Établir, en tenant des conventions du schéma, l'équation différentielle à laquelle obéit uc(t) b. Déterminer la constante de temps t' du circuit. c. Déterminer la valeur de R'. Déterminer la valeur i(0) de l'intensité du courant à la date t=0. Préciser le sens réel de circulation du courant ? 2ème partie On étudie cette fois la réponse à un échelon de tension d'un circuit comportant une bobine inductive (L,r) et une résistance R = 100 W. Le circuit considéré est donné sur la figure 2. La f.e.m de l'alimentation stabilisée utilisée est E = 5V. L'interface reliée à l'ordinateur permet d'étudier les variations de uR(t). 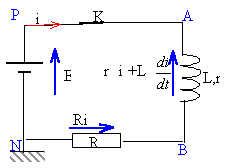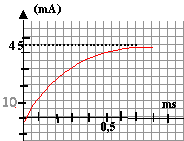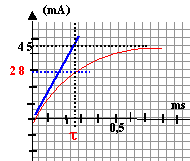La courbe obtenue est donnée sur l'annexe ( graphique 3) A partir de la courbe déterminer la valeur I0 de l'intensité en régime permanent. Déterminer une valeur approchée de la résistance interne r de la bobine Déterminer la constante de temps t du circuit. En déduire une valeur approchée de l'inductance L de la bobine. On ajoute au circuit une bobine identique à la première, les deux bobines étant placées en série. Donner l'expression de la nouvelle constante de temps t' en fonction de L, r, et R. Comparer t et t'. 3ème partie On étudie cette fois la décharge d'un condensateur dans une bobine inductive, on place une résistance R en série avec la bobine. Le schéma est donné fig 3. L'interface de l'ordinateur permet d'étudier uc(t) et uR(t). 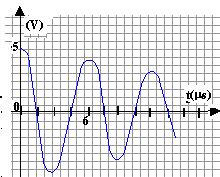On charge le condensateur, puis on bascule l'interrupteur en position 2 puis on déclenche la prise de mesures. On obtient le ci-dessus avec C=5 pF , r=10 W ; L=0,2 H ; E = 5,0 V , R= 100 W. Le logiciel de traitements de données permet d'obtenir l'énergie emmagasinée dans la bobine Wb, l'énergie emmagasinée dans le condensateur Wc, ainsi que l'énergie totale W=Wb+Wc. Établir l'équation différentielle à laquelle obéit la tension uc(t) en tenant compte des conventions de la figure ci-dessus. Déterminer la pseudo-période T des oscillations. Comparer avec la période propre T0 du circuit. Indiquer les expressions littérales permettant le calcul des différentes formes d'énergies à partir des mesures de uc et uR et des caractéristiques du circuit. Attribuer en justifiant les courbes du graphique ci-dessous aux différentes énergies. 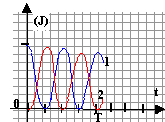Que représente la dérivée de l'énergie totale par rapport au temps dW / dt. L'exprimer en fonction de i(t). Justifier et interpréter l'aspect de la courbe W(t) , en particulier lorsque la tangente est nulle ou extremum. Les oscillations ne s'observent que lorsque la résistance totale du circuit est inférieure à une valeur critique Rc=2 [L/C]½ Estimer la valeur de R donnant le régime critique.  corrigé d'après la courbe ci-dessous : lorsque le condensateur est chargé, la tension à ses bornes est égale à E, donc E=5 V. 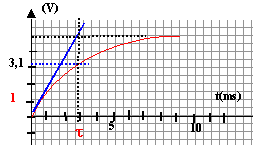la constante de temps vaut t=3 10-3 s. 3 10-3 = RC soit C= 3 10-5 F. à t=0, uc=0 donc E=uR et l'intensité initiale vaut I0 = E/R = 5 /100 = 0,05 A. 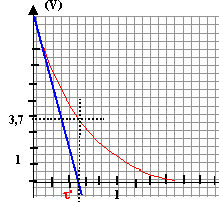à la décharge : uc=R'i ; i = - dq/dt ; q=Cuc soit i = -Cduc/dt uc+R'Cduc/dt =0   la constante de temps vaut t'=0,5 10-3 s. 5 10-4 = R'C soit R'= 5 10-4 / 3 10-5 = 50/3 = 16,7 W . au début de la décharge l'intensité du courant vaut E/R' = 5 / (50/3 )= 0,3A. Son sens est celui indiqué sur le schéma, sens inverse du courant de charge. en régime permanent I0 = 45 mA ; I0 = E/(R+r) = 5/(100+r) = 0,045 soit r = 11,1 W. la constante de temps est proche de t = 0,25 ms = 2,5 10-4 s t = L/(R+r) soit L = t (R+r) = 2,5 10-4*111,1 = 0,028H = 28 mH. t' = 2L/(R+2r) = 0,056/122,2 = 4,6 10-4 s soit environ le double de t . uc=Ri + ri + Ldi/dt avec i = -dq/dt = -Cduc/dt = -Cu'cet di/dt = -Cd²uc/dt² = -Cu"c. uc= -C(R+r)u'c-LCu"c soit LCu"c +C(R+r)u'c+uc= 0 la pseudo-période vaut, d'après le graphe environ 6 10-6 s. la période T0 vaut : 2p [LC]½=6,28 [0,2*510-12]½ = 6,28 10-6 s. énergie stockée par le condensateur : Wc=½Cu²c ; énergie stockée par la bobine Wb = ½Li² avec i = -Cu'c ou encore i = uR/R la dérivée par rapport au temps, de l'énergie totale W=Wc+ Wb donne l'énergie perdue par effet joule dans les résistances. W= ½Cu²c + ½Li² dW/dt = Cuc u'c + Li i' avec C u'c = -i et uc=Ri + ri + Li' dW/dt = -i uc + Li i' = -i (Ri + ri + Li' )+ Li i' = -(R+r)i². courbe 1 : énergie stockée par le condensateur; courbe 2 : énergie stockée par la bobine lorsque la tangente est horizontale, l'un des dipôles, condensateur ou bobine stocke toute l'énergie. valeur de Rc : 2[L/C]½ = 2[0,2/510-12]½ = 4 105 W.

chimie générale (5 points)   L'exercice est un questionnaire à choix multiple. A chaque question peuvent correspondre aucune, une ou plusieurs propositions exactes. Aucune Justification n'est demandée. La notation " zéro" sera attribuée à une réponse fausse ou à l'absence de réponse. Les solutions aqueuses sont à 25'C.   Soit une solution de monoacide AH de concentration C = 1. 10-3 mol.L-1. La transformation de cet acide avec l'eau est totale si : a- pH = 3 ; b- pH = 4 ; c- [H30+] < C ; d- [H30+] > C Soit une solution d'acide AH dont le pKa du couple associé est 3,8. a- l'espèce A- prédomine pour pH = 5,2 b- l'espèce AH prédomine pour pH = 2,0 c- l'espèce AH prédomine pour pH = 4,3 d- aucune des espèces AH et A- ne prédomine pour pH = 7. Soit l'équation de la réaction associée à la transformation : AH + H2O = A- + H30+. La constante d'équilibre K associée à la réaction s'écrit : a- [AH] / ([A-]* [H30+] ); b- [A-] [H30+] / [ AH] [H2O ]) ;c- [A-] [H30+] / [AH] ; d- [AH] [A-] / [H30+] Soient deux solutions d'acides de même concentration et considérées à la même température. L'avancement final de la réaction entre l'acide et l'eau est le plus faible pour la solution d'acide dont : a- la valeur du pH est la plus faible b- la valeur du pH est la plus grande c- la valeur du pKa associé au couple est la plus faible d- la valeur du pKa associé au couple est la plus grande. On réalise le titrage d'une solution d'acide éthanoïque par une solution d'hydroxyde de sodium de concentration 1,0. 10-2 mol/L placée dans une burette graduée. Pour cela, on prélève 20,0 mL d'acide que l'on place dans un bécher en y ajoutant quelques gouttes d'indicateur coloré. On mesure le pH de la solution contenue dans le bécher à chaque volume V d'hydroxyde de sodium versé. L'équation de la réaction de dosage s'écrit a- CH3-COO- + H2O = CH3-COOH + HO- b- CH3-COOH + NAOH = CH3-COO- + H2O + Na+ c- CH3-COOH + HO- = CH3-COO- + H2O d- H30+ + HO- = H2O Pour un volume nul de solution d'hydroxyde de sodium versé, le quotient de réaction initial Qri est égal à: a- Ka ; b- 0 ; c- -2 ; d- 10 L'équivalence est obtenue pour un volume Véq = 12,0 niL d'hydroxyde de sodium. La concentration de la solution d'acide est (mol/L) : a- 1,2.10-2 ; b- 6.10-3 ; c- 6 10-2 ; d- 1,2. 10-3. Le pKa du couple CH3-CO2H / CH3-CO2- associé à l'acide éthanoïque est 4,8. a- le pH à l'équivalence est 7 b- le pH à l'équivalence est supérieur à 7 c- le pH à la demi-équivalence est 2,4 d- le pH à la demi-équivalence est 3,5 L'ajout d'eau distillée dans le bécher contenant la solution à titrer avant le dosage, modifie: a- le volume de d'hydroxyde de sodium versé à l'équivalence b- le pH à l'équivalence c- le pH initial d- le pH à la demi-équivalence Si on réalise ce dosage avec des solutions d'acide éthanoïque et d'hydroxyde de sodium chacune 10 fois moins concentrée que précédenunent: a- le saut de pH au voisinage de l'équivalence est plus grand b- le saut de pH au voisinage de l'équivalence est plus petit c- le pH à la demi-équivalence garde la même valeur d- le pH à l'équivalence ne varie pas. corrigé 1a- bonne réponse. 2 : AH prédomine à pH<pKa ; A- prédomine à pH>pKa ; [A-]=[AH} à pH=pKa. 2a- et 2b- exactes 3c- exacte. 4: plus le pH est petit, plus le pKa est petit, alors plus l'acide est dissocié en ion oxonium H3O+( avancement final grand) 4b- et 4d- vraies. 5b- et 5c- exactes. 6 a- exacte : quotient initial : avant ajout de soude nous avons une solution d'acide éthanoïque CH3-COOH +H2O = CH3-COO- +H3O+ pour laquelle Qri = Ka 7b- exact : 12 10-2 = 20 c soit c = 6 10-3 mol/L. 8b- exact : à l'équivalence solution d'éthanoate de sodium : la base CH3-COO- est présente, donc le pH est supérieur à 7. à la demi équivalence pH= pKa 9c- exact ( l'eau n'apporte pratiquement aucun ion oxonium) 10 b- et 10c- exactes.

chimie organique (5 points)Synthèse d'un arôme   I Identification des composés organiques : Le méthanoate de 2-méthylpropyle est un arôme à l'odeur de framboise.La formule semi-développée de ce composé organique (C) est H-COO-CH2-CH(CH3)2. Nonnner et encadrer sur la formule semi-développée la fonction chimique de ce composé. Le composé (C) peut être obtenu par une réaction lente entre un acide carboxylique ( A) et un autre composé organique ( B) a) Ecrire les formules semi-développées des composés ( A) et ( B) Les nommer b) Ecrire l'équation qui, à partir de (A ) et de ( B), permet d'obtenir le composé (C) Le composé ( B) peut être oxydé par une solution acidifiée de permanganate de potassium. Couple MnO4- / Mn2+. - Ecrire l'équation de cette réaction et nommer le composé organique obtenu.. II Préparation de l'arôme : on introduit dans un ballon 0,5 mol de (A) , 0,5 mol de ( B), 2 mL d'acide sulfurique et quelques grains de pierre ponce.. On réalise un montage de chauffage à reflux. La température du chauffe-ballon est réglée à 65 °C. Représenter le schéma légendé d'un montage de chauffage à reflux. Quel est l'intérêt d'un tel montage ? Quel est le nom de la réaction chimique réalisée entre ( A) et ( B) ? Quelles sont ses caractéristiques ? On suit l'évolution temporelle de cette réaction, réalisée à volume constant, en déterminant, toutes les 6 minutes, la quantité de matière n (C ) formée. On obtient les résultats suivants: t(min) 0 6 12 18 24 30 36 42 48 54 60 66 n(C) en mol 0 0,14 0,21 0,25 0,27 0,29 0,31 0,33 0,33 0,33 0,33 0,33 - Définir la vitesse volumique v(t) de formation du composé ( C). En déterminant les vitesses volumiques aux instants t1 = 18 min et t2 = 42 min, on trouve v(tl) > v(t2). Quel est le facteur cinétique responsable de la variation de v(t) au cours du temps ? Définir et calculer le rendement de la réaction entre ( A) et ( B ). La valeur numérique du rendement varie-t-elle (justifier les réponses ) a) En prolongeant la durée du chaufface ? b) En doublant les quantités de matière de deux réactifs ? c) En augmentant la quantité d'acide sulfurique ? d) en augmentant de 20 °C la température initiale du chauffe-ballon? Lors de la synthèse industrielle du méthanoate de 2-méthylpropyle, on préfère utiliser un autre réactif organique ( A') réagissant avec ( B). Quel est le nom de ce réactif ( A') ? Pourquoi le préfère-t-on ?   corrigé fonction ester :H-COO-CH2-CH(CH3)2. (A) est l'acide formique ou méthanoïque HCOOH ; (B) est l'alcool 2-méthylpropan-1-ol HOCH2-CH(CH3)2. HCOOH + HOCH2-CH(CH3)2 = H-COO-CH2-CH(CH3)2 + H2O HOCH2-CH(CH3)2 + H2O = HOOC-CH(CH3)2 + 4H+ + 4e-. MnO4- + 8H+ + 5e-= Mn2++ 4H2O. 5 HOCH2-CH(CH3)2 + 4 MnO4- + 12H+ --> 5HOOC-CH(CH3)2 +11H2O +4 Mn2+. 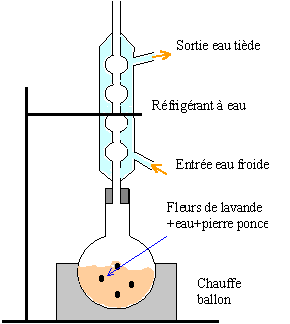on obtient l'acide 2-méthylpropanoïque le chauffage à reflux permet de travailler à température modérée ( la vitesse de la réaction augmente) tout en évitant les pertes de matière. estérification, lente limitée par l'hydrolyse de l'ester et athermique vitesse volumique : v =1/V dn(C) / dt avec V : volume de la solution contenant les réactifs. cette vitesse diminue au cours du temps car les quantités de matière des réactifs diminuent. rendement : Qté de matière expérimentale / Qté de matière théorique = xfin / xmax = 0,33 / 0,5 = 0,66. l'équilibre étant atteint à t=48s, le rendement ne peut pas augmenter en continuant de chauffer. En doublant les quantités initiales des réactifs, en augmentant la quantité de catalyseur, en travaillant à température plus élevée, on atteint plus rapidement l'équilibre, sans changer le rendement. (A') est le chlorure de méthanoyle HCOCl. Dans ce cas la réaction entre le chlorure de méthanoyle et l'alcool est totale. retour - menu