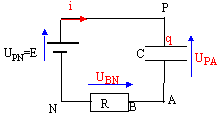
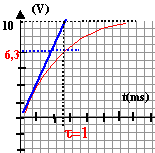
Données : R= 1 kW ; E=10 V ; C= 1 mF.

On réalise la charge d'un condensateur de capacité C en le montant en série avec un conducteur ohmique de résistance R et un générateur de force électromotrice E.. Le condensateur est initialement déchargé et à t=0 on commence la charge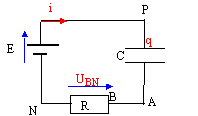

.

1. Reproduire le schéma en fléchant les tensions u_PN, u_PA, u_NB
   -- Exprimer la relation liant ces tensions.
   - En déduire l'équation différentielle gouvernant l'évolution de la tension u_C=u_PA aux bornes du condensateur.
2. Nous allons déterminer par le calcul l'évolution de cette tension u_C à des intervalles de temps dt = 10^-4 s.
   - A t=0 que vaut u_C ?
   - Exprimer de façon générale la dérivée de u_C par rapport au temps du_C / dt en fonction de E, u_C, R et C. En déduire la valeur initiale du_C / dt (t=0) de cette dérivée.
   - Recopier sur votre copie le tableau ci-dessous en complétant la première colonne.

   t(s)	0	10-4	2 10-4	3 10-4	4 10-4
   uC
   duC / dt

   La méthode d'Euler permet par itérations successives de calculer u_C aux différentes dates du tableau. On a en effet u_C(t+dt) = u_C(t) + du_C. Il suffit de calculer du_C pendant une durée suffisamment petite devant la durée totale du phénomène.
   - Effectuer en détail sur votre copie le calcul de u_C (0+dt) puis de du_C / dt (0+dt) pour la date t=0+dt = 10^-4 s. Finir de compléter le tableau.
   - tracer grâce aux valeurs du tableau la courbe u_C=f(t). Echelle 1cm pour 10^-4s et 1 cm pour 1V.
   - Tracer sur ce graphe la tangente à la courbe à t=0 : du_C / dt (0).
   - Prolonger en pointillé ce graphe en imaginant l'évolution temporelle de u_C après un temps suffisamment long. Mentionner toute valeur utile à la compréhension de votre travail.

---

corrigé

---

U_NB= -U_BN= -Ri = U_NP +U_PA+U_AB

-Ri = -E + U_C +0 avec i = dq/dt = CdU_C/dt = Cu'_C.

-RCU'_C = -E + U_C ou RCU'_C + U_C =E

U'_C + 1/(RC) U_C =E / (RC) avec RC = 10³*10^-6 = 10^-3 s^-1.

dU_C/dt + 10³ U_C = 10³E = 10⁴.

or dt = 10^-4 s soit dU_C=1-0,1U_C.(1).

à t=0 : U_C=0 (condensateur non chargé) ; dU_C=1 et dU_C/dt(t=0)= 1 / 10^-4 = 10⁴Vs^-1.

U_C(0+dt) = U_C(t=0) + dU_C=0+1 =1.

t(s)	0	10-4	2 10-4	3 10-4	4 10-4
uC(V)	0	1	1,9	2,71	3,44
duC / dt (Vs-1)	104	9 103	8,1 103	7,3 103	6,56 103

à t=10^-4 s : U_C=1; dU_C=1-0,1*1 = 0,9 et dU_C/dt= 0,9 / 10^-4 = 9 10³Vs^-1.

U_C(2 10^-4) = U_C(10^-4) + dU_C=1+0,9 = 1,9 V.

---

à t=2 10^-4 s : U_C=1,9; dU_C=1-0,1*1,9 = 0,81 et dU_C/dt(= 0,81 / 10^-4 = 8,1 10³Vs^-1.

U_C(3 10^-4) = U_C(2 10^-4) + dU_C=1,9+0,81 = 2,71 V.

---

à t=3 10^-4 s : U_C=2,71; dU_C=1-0,1*2,71 = 0,73 et dU_C/dt= 0,73 / 10^-4 = 7,3 10³Vs^-1.

U_C(4 10^-4) = U_C(3 10^-4) + dU_C=2,71+0,73 = 3,44 V.

---

à t=4 10^-4 s : U_C=3,44; dU_C=1-0,1*3,44 = 0,656 et dU_C/dt = 0,656 / 10^-4 = 6,56 10³Vs^-1.

U_C(5 10^-4) = U_C(4 10^-4) + dU_C=3,44+0,656 = 4,1 V.

retour - menu