|
Un appareil photographique comporte deux éléments essentiels :
l’objectif et la pellicule. On modélise :
- l’objectif par une lentille mince convergente (L) de centre
optique O ; on appelle F et F’ les foyers principaux, respectivement
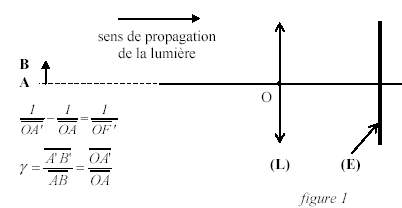
objet et image, de cette lentille, dont la distance focale est :OF'
=+50 mm ;
- la pellicule par un écran (E), où se forme l’image réelle de
l’objet photographié (figure 1).
L’objectif est conçu pour pouvoir déplacer la lentille (L) par
rapport à la pellicule.
- On photographie un objet AB situé à une très grande
distance de (L). En le considérant « à l’infini », et pour avoir une
image nette, à quelle distance OA’ de l'écran (E) se trouve la lentille
(L) ?
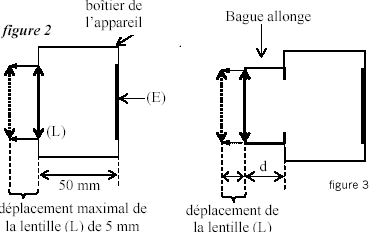
- Pour obtenir des images, sur l’écran (E), d’objets plus
rapprochés de (L), il est nécessaire d’effectuer une mise au point,
c’est-à-dire de faire varier la distance lentille – écran (voir la
figure 2 ).
Si l’objet AB à photographier se rapproche de (L), la
distance entre la lentille et l’écran doit-elle augmenter ou diminuer ?
Justifier à l’aide d’un schéma.
- L’objectif permet d’augmenter de 5 mm au maximum la
distance entre la lentille et la pellicule par rapport à sa position
quand l’objet est « à l’infini ». À quelle distance doit se trouver un
objet pour que son image soit nette sur la pellicule quand la distance
lentille - écran est maximale ?
- Calculer le grandissement g dans ces
conditions.
- On veut photographier une carte postale de format 10 cm ×
15 cm. En la plaçant à 55 cm de (L) dans un plan perpendiculaire à
l’axe optique de la lentille (L), le grandissement vaut 0,1 en valeur
absolue. Quelles seraient les dimensions de son image sur la pellicule
de format 24 mm × 36 mm ?
- On veut que les dimensions de l’image de la carte postale soient 24
mm × 36 mm. Calculer la valeur absolue du grandissement g souhaité.
- Pour simplifier les calculs numériques, prendre : g
= -1/4. Calculer alors la distance OA à laquelle on
doit placer la carte postale, ainsi que la distance OA’ entre la
lentille et l’écran.
- On ne peut pas obtenir la distance OA’ nécessaire trouvée à la
question précédente avec le seul objectif de l’appareil photographique.
Il est toutefois possible d’adapter, entre l’objectif et le boîtier de
l’appareil photographique, un ou plusieurs tubes creux appelés « bagues
allonges » de longueur d (figure 3 ci-dessus). Disposant de bagues
allonges de longueurs 5 mm, 10 mm et 20 mm, indiquer :- laquelle ou
lesquelles choisir ; - comment procéder pour que l’image de la carte
postale soit nette sur la pellicule avec pour grandissement g = -1/4.
corrigé
Objet à l'infini : donc l'image se
trouve dans le plan focal image OA' = OF' = 0,05 m
l'objet se rapproche de la lentille, alors la distance
lentille- pellicule augmente.
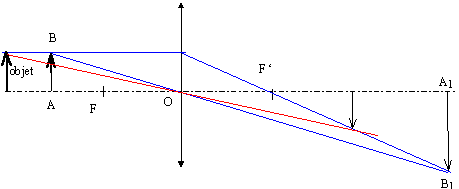
appliquer la formule de conjugaison : ( ce qui est écrit en
gras et en bleu est une grandeur algébrique)
OA' = (5+50)10-3
m ; OF' = 0,05 m
1/OA = 1/OA' - 1/OF
'= 1000 / 55 -1000 / 50= -1,818
OA = -0,55
m.
grandissement g =OA' /OA
= 55 10-3 / (-55 10-2) = -0,1.
dimensions de l'image de la carte placée à 55 cm de la
lentille :
10 cm *0,1 = 1 cm et 15
cm*0,1 = 1,5 cm.
valeur absolue du grandissement :|g| =2,4 / 10 = 0,24 ;|g|
=3,6 /15 = 0,24 ;
g =OA'
/OA = -0,25 soit OA = -4OA'
appliquer la formule de conjugaison :
1/OF '=1/OA' -1/OA
= 1/OA' +1(4OA') =5 / OA'
.
OA' = 5 /4OF '=1,25*50 = 62,5 mm
OA = -4*62,5 = -25 cm.
|
allonge (mm)
|
distance lentille-pellicule (mm)
|
|
5
|
mini : 5+50 = 55
maxi : 5+55 =60
|
|
10
|
mini : 10+50 = 60
maxi : 10+55 =65
|
|
20
|
mini : 20+50 = 70
maxi : 20+55 =75
|
l'allonge de 10 mm convient.
en diaphagmant, on élimine les rayons trop inclinés sur l'axe
optique principal ( on se rapproche des conditions de Gauss) : l'image
sera plus nette sur la pellicule.
|


