|
|
||||||
|
|
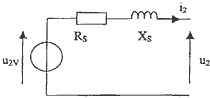
Le sujet propose d'étudier l'alimentation en énergie d'un moteur à courant continu de faible puissance et de réguler sa vitesse de rotation. 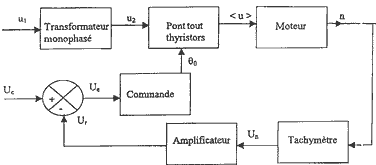 Transformateur monophasé 50 Hz : Les mesures effectuées avec des appareils numériques ont donné les résultats suivants : essai en courant continu au primaire : U1DC = 5 V ; I1DC = 10 A essai à vide sous tension primaire nominale : U1N = 240 V; I1V = 1 A ; P1V = 10 W ; U2V= 24 V essai en court-circuit sous tension primaire réduite :U1CC = 24 V I2CC = 30 A ; P1CC = 36 W essai sur charge résistive et sous tension primaire nominale : U1N = 240 V I2 = I2CC = 30 A
corrigé |
|||||
|
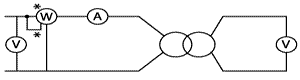
Il convient de brancher les appareils en longue dérivation, car à vide le courant est faible et la tension est nominale.
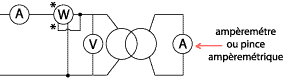
m = U2V/U1N= 24/240=0,1. Pour déterminer les pertes Joule, il nous faut calculer la résistance des enroulements du primaire. Elle se déduit de l'essai en courant continu : r1 = U1DC / I1DC = 5/10 = 0,5 W. Les pertes Joules lors de l'essai à vide valent donc : pJV = r1I²1V= 0,5* 1²= 0,5 W. Or lors de l'essai à vide on mesure les pertes joule à vide et les pertes fer P1V=10 W ; les pertes Joule ne représentent que 5% des pertes totales du transformateur lors de cet essai. On peut donc les négliger. On considère donc PferV = P1V = 10 W Sans négliger les perte Joules, les pertes fer s'élèvent à 9,5 W lors de l'essai à vide. essai en court-circuit : Il convient d'adopter un montage courte dérivation car le courant est important (nominal) lors de l'essai en court-circuit.
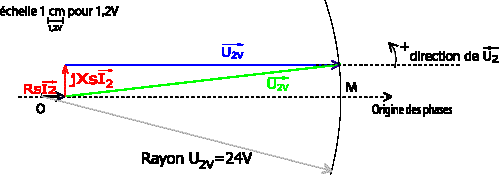
Par hypothèse : Pfer = kU²1. PferV / U²1V = PferCC / U²1CC = k soit PferCC= PferVU²1CC / U²1V = 10*24²/240² = 0,1 W. or PferCC/ P1CC = 0,1/ 36 = 0,28% Les pertes fer sont négligeables lors de l'essai en court circuit. P1CC = PferCC+ PJCC =36 W on en déduit : PJCC =36 W. RS= P1CC/I2CC=36/30² = 40 mW. essai en charge : On prend le courant I2 à l'origine des phases. On peut alors tracer le vecteur RSI2. qui a pour longueur RSI2 = 0,04 * 30 = 1,2V et pour sens et direction ceux de I2. On trace au bout de RSI2 le vecteur qui a pour longueur XsI2 = 0,08*30 = 2,4 V et qui se trouve en quadrature avant par rapport àI2. Il nous reste ensuite 2 informations à exploiter : U2V = m.U1 = 24 V U2 et I2 sont en phases (car la charge est résistive) La première information nous permet de tracer le cercle de centre O et de rayon U2v = 24 V sur lequel se trouve le point de fonctionnement. La seconde information nous permet de tracer la direction de U2. L'intersection du cercle et de la droite nous donne le point M de fonctionnement. On peut alors tracerU2 et U2V. . La mesure de U2 nous donne U2 = 19 cm = 22,8 V
rendement h =Pu / Pa . Or Pu = U2I2 (charge résistive ) Pa = Pu + pJoule + pfer= 22,8*30+35,9+9,5 = 22,8*30 / 729,4 = 0,94 (94%)
|
||||||
|
Moteur à courant continu alimenté par un pont tout thyristors Moteur à courant continu : On relève sur la plaque signalétique du moteur les indications suivantes :- Induit : 0,2 W ; 20 V ; 10 A. - 160 W ; 1 000 tr/min ;- Inducteur à aimants permanents. ;- Machine compensée.
Pont tout thyristors : Le secondaire du transformateur alimente le pont dont le schéma est donné : 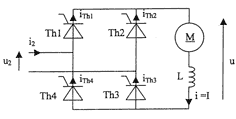 Les thyristors sont supposés parfaits. La commande des gâchettes n'est pas représentée. Une sonde de courant de sensibilité 100 mV/A est utilisée pour visualiser à l'oscilloscope le courant dans la charge. Simultanément, on visualise la tension u aux bornes de la charge. L'oscillogramme obtenu est représenté : 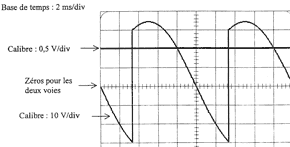 La charge du pont redresseur est constituée de l'induit d'un moteur à courant continu à aimants permanents et d'une bobine de lissage considérée comme parfaite. La force électromotrice E du moteur est proportionnelle à la vitesse de rotation E = 18 10-3n (E en V et n en tr/min). La résistance de l'induit du moteur est R = 0,2 W. Le moteur entraîne une charge lui imposant un courant d'intensité supposée constante.
corrigé Pour une MCC on a toujours E = k'F W (avec k' = cste). Ici la machine est à aimants permanents, donc F = cste d'où E = k''W (avec k'' = cste). Or W =2pn/60 d'où E = k''2pn/60 soit E = k.n. Pa=UI= 20*10=200 W; h =Pu / Pa 160 /200 = 80%. Bilan de puissance : Pa = Pu + pJoules + pfer + pméca avec pJoules + pfer + pméca = pertes et pfer + pméca = pc donc Pertes = Pa - Pu = 200 - 160 = 40 W pc = Pertes - pJoules or pJoules = RI² = 0,2 10² = 20 W d'où pc = 40 - 20 = 20 W. Tu = Pu/W = 60Pu/(2pn) = 1,53 Nm. U = E + RIdonne E = U - RI= 20 - 0,2* 10= 18 V. k=E/n = 18 / 1000
= 18 10-3 V.min.tr-1
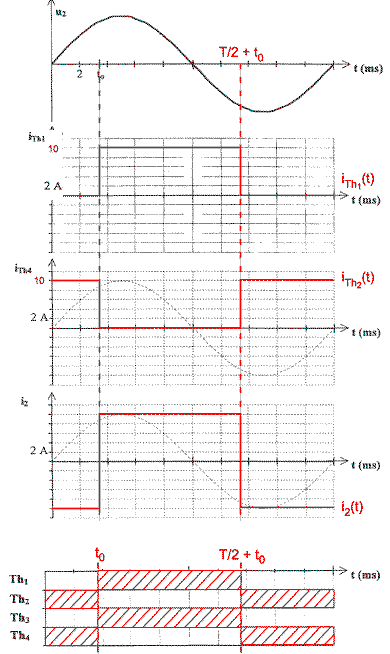
Le signal représentant I vaut 0,5 V * 2 divisions = 1 V On a donc I= 1 / 100 10-3 = 10 A. avec 100 10-3 mV/A la sensibilité de la sonde Sur la figure on lit t0 = 1,65 carreaux = 1,65 2 = 3,3 ms q0 = 360t0/T= 360*3,3 / 20 = 58°. 2.2.a. Voir document réponse 2 Les Thyristors marchent par paires : (Th1, Th3) et (Th2, Th4). u = uM + uL où uM est la tension aux bornes du moteur. soit u = E + Ri + uL car uM = E + Ri Reprenons l'égalité u = uM + uL et passons aux valeurs moyennes : <u> = <uM + uL> = <uM> + <uL> Or <uL> = 0 La valeur moyenne de la tension aux bornes d'une bobine alimentée par un courant périodique est nulle. Donc <u> = <uM> Or uM = E + Ri et i = I = cste E = k n varie très peu au cours d'une période (20 ms) et peut être considérée constante sur cet intervalle. Donc uM <uM>
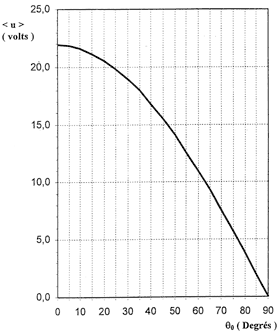
Sur la courbe figure 4, on peut lire <u> = 11,5 V
On a vu que uM = <u> = E + RI Soit E = <u> - RI avec E = kn, il vient kn = <u> - RI d'où n = (<u> - RI) / k = (11,5-0,2*10) / 18 10-3 =528 tr/min.
|
||||||
|
Régulation de la vitesse de rotation du moteur : Pour éviter des variations importantes de vitesse lors d'une perturbation, on réalise la régulation par le système bouclé schématisé sur la figure : 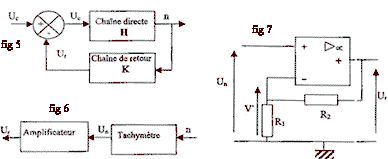 Chaîne de retour - menu : La chaîne de retour - menu est constituée par l'ensemble tachymètre - amplificateur (figure 6 ). Le tachymètre délivre une tension Un proportionnelle à la vitesse de rotation du moteur : Un = 510-3 n (n en tr/min et Un en V). L'amplificateur opérationnel du montage amplificateur (figure 7 ) est supposé parfait et fonctionne en régime linéaire.
Régulation de vitesse : Ue est une tension de commande qui sert à régler l'angle de retard à l'amorçage des thyristors et donc à régler la tension moyenne < u > à la sortie du pont. La relation liant la tension U1 à la tension moyenne < u > est < u > = 100 Ue. On négligera la chute de tension dans l'induit du moteur ; la valeur de < u > est alors pratiquement proportionnelle à la vitesse de rotation : < u > = 2010-3 n (< u > en V et n en tr/min)
corrigé Chaîne de retour - menu : L'amplificateur opérationnel de la figure 7 possède un rebouclage de sa sortie sur son entrée inverseuse. Il fonctionne donc en régime linéaire et on peut écrire : V + = V - Or ici, V + = Un donc Un = V - D'après le pont diviseur avec R1 et R2, on a :V - = R1 / (R1 + R2) Ur. d'où ,Ur = (1 + R2/ R1) Unsoit Ur / Un = (1 + R2/ R1) K=Ur/n ; or Un = 5 10-3 n ; K= 5 10-3Ur / Un = 5 10-3(1 + R2/ R1) R2 = R1
(K/5 10-3-1 )=104(0,01/5 10-3-1
)= 10 kW.
L'énoncé donne <u>= 20 10-3 n soit n / <u>= 1 / 20 10-3 = 50 tr min-1 V-1. or H = n / ueet <u>= 100 ue soit H= 100 n / <u> = 100*50= 5000 tr min-1 V-1. ue = 0,01<u> et <u>= 20 10-3 n soit ue = 0,01 *20 10-3 *1000 = 0,2 V Ur=K.n (chaîne de retour - menu) Ur = 0,01* 1000 = 10 V. Le soustracteur de l'asservissement amène Ue = Uc - Ur donc Uc = Ue+ Ur= 0,2 + 10= 10,2 V. Si n diminue alors Ur = K.n diminue également. Si Ur diminue, alors comme Uc reste constante, Ue = Uc - Ur augmente. Alors n = H.Ue (chaîne directe) augmente. Donc si la vitesse diminue, le rebouclage tend à la faire augmenter. Le système réagit donc pour "contrer" l'action de la perturbation. L'intérêt du rebouclage est ici d'obtenir un système moins sensible aux perturbations.
|
||||||
|