|
Antilles 06/00 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
L'exercice a pour but de comparer le mouvement d'une particule chargée traversant un champ électrique et le mouvement d'un projectile lancé horizontalement dans le champ de pesanteur terrestre. Données : masse de l'électron m = 9,110-31 kg ; charge de l'électron q = - e = - 1,6.10-19 C ; champ de pesanteur g = 9,81 m .s -2 Déviation d'un faisceau d'électrons dans un champ électrique uniforme : Le champ électrique est créé par un condensateur plan constitué de deux plaques parallèles et horizontales (P l et P2) reliées à un générateur de tension constante U=205 V et séparées d'une distance d, comme l'indique la figure ci-dessous. 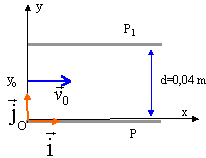 Tous les électrons pénètrent dans le champ, supposé uniforme, à l'ordonnée y0 et sont animés de la même vitesse parallèle aux plaques.
Mouvement d'une bille lancée horizontalement dans le champ de pesanteur terrestre : Une bille homogène de masse M est lancée horizontalement avec une vitesse initiale. A l'instant initial, son altitude par rapport au sol est y0 comme l'indique la figure 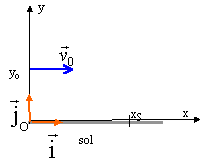
Comparaison des mouvements de ces deux corps :
force électrique F =|q| E= 1,6 10-19 * 5125 = 8,2 10-16 N. poids = mg = 9,1 10-31 *9,8 = 9 10-30 N très inférieur à la force électrique. les vecteurs sont écrits en gras et en bleu. la seconde loi de Newton s'écrit q E = ma soit a = q/ m E. force électrique dirigée vers le bas ; la charge est négative alors le champ et la force sont colinéaires de sens contraire : champ électrique vertical vers le haut le champ pointe vers le plus petit potentiel : donc plaque supérieure au plus petit potentiel.
a1 ( 0 ; -eE/m) ; v0 ( v0 ; 0) ; OM0 ( 0 ; y0) vitesse v primitive de l'accélération ( v0 ; -e/mE t) position OM primitive de la vitesse( x = v0 t ; y = -0,5 e/mE t² +y0) équation cartésienne de la trajectoire : y = -0,5 e/m E x² / v0 ² +y0 A1 = - e/mE / (2v0²) avec a1 = -e/m E soit A1 = a1 / (2v0²) A1 =
-0,5 *1,6 10-19 / 9,1 10-31 * 5125 / 2,25 1014
= -2
a2 = g verticale vers le bas norme 9,8 m/s² vitesse initiale v0 ( v0 ; 0) ; OM0 ( 0 ; y0) vitesse v primitive de l'accélération ( v0 ; -g t) position OM primitive de la vitesse( x = v0 t ; y = -0,5 g t² +y0) équation cartésienne de la trajectoire : y = -0,5 g x² / v0² + y0 A2 = - g / (2v0²) = -0,5 *9,8 / 196 = -0,025 au sol y =0 ; xS =7,75 et y0 =1,5 0 = A2
*7,75² +1,5 d'où A2 = - 1,5 / 7,75² = -0,025.
la force électrique F= qE est indépendante de la masse. l'accélération a1 = -e/mE est inversement proportionnelle à la masse. le poids est proportionnel à la masse . a2 = g est indépendant de la masse. |
|||||
|
|
||||||
|