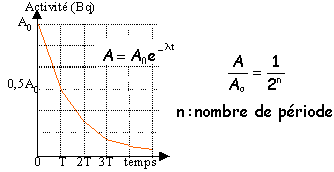datation au carbone 14 :

 Des fragments d'os et de charbon de bois ont été prélevés dans un site préhistorique. On mesure l'activité du carbone 14 des résidus d'os et de charbon, afin d'en déterminer l'âge. Le carbone 14 ¹⁴C (Z=6) est produit constamment dans l'atmosphère suite au bombardement de l'azote ¹⁴N (Z=7) par les neutrons crées dans la haute atmosphère par les rayons cosmiques. Les plantes assimilent aussi bien l'isotope ¹²C que l'isotope ¹⁴C.

Les abondances respectives de ces deux isotopes sont les mêmes dans le dioxyde de carbone de l'atmosphère et les êtres vivants. A la mort de ces derniers, il n'y a plus d'assimilation ; le carbone 14 radioactif se désintègre. Sa demi-vie ou période est égale à 5568 ans.

L'activités du carbone 14 dans les résidus d'os donne 110 d'ésintégrations par heure et par gramme de carbone. L'échantillon de référence donne 13,6 désintégrations par minute et par gramme de carbone.

1. Rappeler la définition de la demi-vie.
2. Construire la courbe donnant l'activité A en fonction du temps.
3. Déterminer à partir du graphe l'âge des résidus d'os.
4. Montrer que l'âge t des résidus d'os, exprimé en années, peut-être calculer par la relation t = 8033 ln ( A₀/A). calculer t. 

pile atomique :

Dans une pile atomique l'une des réactions est la suivante :

1. Déterminer en justifiant les valeurs de Z et x.
2. Calculer la perte de masse.
   - Calculer en joule, et en MeV, l'énergie libérée par la fission d'un noyau d'uranium 235.
3. Calculer l'ordre de grandeur de l'énergie libérée par la fission de 5 g d'uranium.
   - Calculer la masse de pétrole libérant, par combustion, la même énergie.

Masses des atomes ²³⁵ U : 234,993 32 u ; ⁹⁴Sr : 93,894 46 u ; ¹⁴⁰Xe : 139,891 94 u ; neutron : 1,008 66 u ; 1u = 1,66 10^-27 kg.

pouvoir calorifique du pétrole : 42 MJ/ kg ; 1 MeV = 1,6022 10^-13 J ; c = 3 108 m/s ; N= 6,022 10²³ mol^-1 ;

La Terre est bombardée en permanence par des particules très énergétiques venant du cosmos. Ce rayonnement cosmique est composé notamment de protons très rapides. Les noyaux des atomes présents dans la haute atmosphère « explosent » littéralement sous le choc de ces protons très énergétiques et, parmi les fragments, on trouve des neutrons rapides. Ces neutrons rapides peuvent à leur tour réagir avec des noyaux d'azote de la haute atmosphère. Lors du choc, tout se passe comme si un neutron rapide éjectait un des protons d'un des noyaux d'azote et prenait sa place pour former un noyau Y₁. Ce noyau Y₁ est un isotope particulier du carbone, le carbone 14, qui est radioactif : en émettant un électron et une particule non observable, l'antineutrino, il se décompose en un noyau Y₂. La période ou demi-vie du carbone 14 est 5 570 ans. Comme le rayonnement cosmique bombarde la Terre depuis longtemps, un équilibre s'établit entre la création et la décomposition du carbone 14 : il y a autant de production que de décomposition si bien que la teneur en carbone 14 de tous les organismes vivants reste identique au cours du temps. Ce carbone s.oxyde en dioxyde de carbone qui se mélange à celui de l.atmosphère, à celui dissous dans l.eau, etc. et sera métabolisé par les plantes et à travers elles par tous les organismes vivants. Dans chaque gramme de carbone de l'atmosphère ou des organismes vivants, les atomes de carbone sont en très grande majorité des atomes de carbone 12, mais il y a 6,8.10¹⁰ atomes de carbone 14.

D.après I. Berkès « La physique du quotidien »

On donne, pour différents noyaux :

H : Z = 1 ; He : Z = 2 ; C : Z = 6 ; N : Z = 7 ; O : Z = 8.

1. Réactions nucléaires dans la haute atmosphère
   - Le proton est représenté par le symbole ¹₁H . Justifier cette écriture.
   - L'.équation de la réaction qui a lieu lorsque le neutron rapide éjecte un des protons du noyau d'azote peut s'écrire : ₀¹n + ¹⁴₇N-->^A_ZY₁ + ¹₁H . Énoncer les lois de conservation qui régissent une réaction nucléaire.
   - Vérifier que,comme l'indique le texte, on obtient bien du carbone 14 ; préciser la composition de ce noyau.
   - Désintégration du carbone 14 : Ecrire l'équation de la réaction qui a lieu lorsque un noyau de carbone 14 se décompose à son tour, en précisant le type de radioactivité du carbone 14. On ne tiendra pas compte de l'antineutrino produit.
   - Identifier l.élément Y₂ formé.
2. Phénomène de décroissance radioactive
   - Donner la définition du temps de demi-vie t½ .
   - Donner la relation entre la constante radioactive l et le temps de demi-vie t½.
   - Par une analyse dimensionnelle, déterminer l'unité de l.
   - A l'aide du texte, calculer sa valeur en unité SI, pour la désintégration du carbone 14.
3. Soit N le nombre moyen de noyaux radioactifs restant dans un échantillon à la date t. Le nombre moyen de désintégrations pendant une durée Dt courte devant t½ est -DN (opposé de la variation de N). Ce nombre moyen de désintégrations est donné par la relation : -DN = l N D t. Déterminer le nombre de désintégrations par minute et par gramme de carbone d'un organisme vivant à partir du moment de sa mort.
   - Même question pour un échantillon de 1 gramme et une durée de 1 seconde. Quelle unité peut-on attribuer à ce dernier résultat ?
4. Datation au carbone 14
   - Comment expliquer que la quantité moyenne de carbone 14 par kilogramme de matière (ou teneur) reste constante pour tous organismes en vie ?
   - Comment évolue la teneur en carbone 14 quand un organisme meurt ? Justifier la réponse.
   - On date par la méthode du carbone 14 un morceau de sarcophage en bois trouvé dans une tombe de l'Egypte ancienne. Dans cet échantillon, on mesure en moyenne 10 désintégrations par minute et par gramme de carbone. Déterminer le nombre de noyaux de carbone 14 subsistant dans cet échantillon.
   - Proposer un âge pour le bois de ce sarcophage.