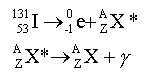|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||
|
||||||||||||||||||||
|
|
L'image scintigraphique utilise des traceurs et des marqueurs. Un traceur est une substance qui peut se localiser de façon sélective au niveau d'une structure particulière de l'organisme. Un marqueur est une substance radioactive qui se prète aisément à une détection externe. Il émet des rayonnement g qui sont détectés à l'extérieur de l'organisme à l'aide d'une gamma-caméra. Pour réaliser des scintigraphie thyroïdiennes, l'iode radioactif est le traceur de référence. On utlise soit l'iode 131 soit l'iode 123. A. Généralités :
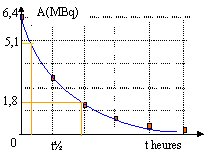
B. Utilisation de l'iode 131 émetteur (b-, g) de demi vie t½= 8 jours :
C. Utilisation de l'iode 123 émetteur g pur de demi vie t½ = 13,2 h :
le noyau d'ode 131 compte : 53 protons ; 131-53 = 78 neutrons.
conservation de la charge : 1+52 = 53 + Z d'où Z =0 conservation du nombre de nucléons : 2+122 = 123 + A d'où A=1 la particule 01X est un neutron. les deux isotopes de l'iode doivent être radioactifs et émetteur g. L'énergie de liaison d'un noyau est l'énergie qu'il faut fournir quand il est au repos pour le casser en ses différents nucléons obtenus au repos et sans interactions entre eux. iode 131 : défaut de masse53*1,007 28 + 78* 1,008 66-130,877 05= 1,184 27 u énergie (J) =1,18427*931,5 =1103,14 MeV puis diviser par le nombre de nucléons : 1103,14 /131 = 8,42 MeV / nucléons iode 123 : défaut de masse53*1,007 28 + 70* 1,008 66-130,877 05= 1,1155 u énergie (J) =1,1155*931,5 = 1039 MeV puis diviser par le nombre de nucléons : 1039 /123 = 8,45 MeV / nucléons les valeurs
trouvées sont inférieures au maximum 8,8 MeV /nucléons : ces deux
isoptopes sont donc instables,
émision d'électrons et de rayons gamma. conservation de la charge : 53 = -1 + Z d'où Z= 54 conservation du nombre de nucléons : 131 = 0 +A d'où A = 131 X est un isotope du xénon énergie libérée par désintégration : |perte de masse| = 130,877 05-(130,875 45+5,485 10-4) = 1,051 10-3 u énergie libérée: 1,051 10-3* 931,5 = 0,978 MeV. activité : A = A0 exp ( - lt) = A0 exp ( - t / t ) l : constante radioactive telle que l t½ = ln2 t½ = 8 jours ; l = ln(2) / 8 = 0,0866 jour-1; t = 1/l= 11,541 jours. activité à t = 1
jour : A = A0 exp ( -1*0,0886) = 0,915 A0.
t½ = 13,2 h ; l = ln(2) / 13,2 = 0,0525 h-1; t = 1/l= 19,04 h= 6,855 104 s.
|
|||||||||||||||||||
|