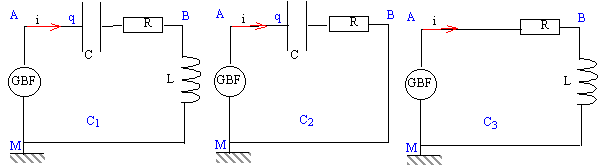
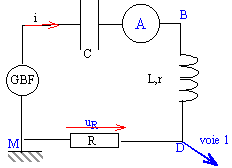
On se propose de déterminer l'inductance d'une bobine par deux méthodes différentes.

partie A :

Un résistor de résistance R, un condensateur de capacité C, une bobine d'inductance L de résistance négligeable appartiennent à différents circuits C₁, C₂ , C₃ alimentés par un générateur délivrant une tension en crénaux.

1. Tracer sur chacun des circuits les flèches représentant les tensions u_R=Ri et u_C=q/C.
2. Avec l'oscilloscope, pour chacun des circuits, on visualise u_R ou u_C.
   

   

   Compléter le tableau ci-dessous en indiquant:
   - le circuit utilisé.
   - le phénomène physique observé
   * phénomène 1 : charge décharge d'un condensateur à travers un résistor
   * phénomène 2 : charge décharge oscillante d'un condensateur à travers un résistor
   * phénomène 3 : autoinduction.

   numéro de l'oscillogramme	circuit électrique	phénomène physique
   1
   2
   3
   4

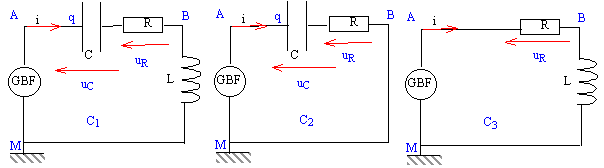
partie B:

On considère le circuit C₁ dont le générateur délivre maitenant une tension sinusoïdale. Le circuit est le siège d'oscillations forcées.

1. Pourquoi dit-on que ces oscillations sont forcées ?
2. On veut visualiser la tension u_R. Reprendre le circuit en plaçant correctement le résistor et en indiquant les branchements de l'oscilloscope. Placer un ampèremètre.
3. L'amplitude de la tension d'alimentation est maintenue constante, on fait varier la fréquence f. L'amplitude u_R prend une valeur maximale pour une valeur particulière de f notée f₀. Comment appelle-t-on cette situation ?
4. Pour la fréquence f₀ l'oscillogramme correspondant à u_R est le suivant :

   Déterminer f₀.

5. L'ampèremètre indique 2 mA pour cette fréquence f₀. Cette valeur correspond-elle à l'intensité maximale ? à l'intensité instantanée ? ou à l'intensité efficace ?
6. Calculer pour cette fréquence f₀, l'impédance du dipôle RLC série.

---

. .

---

corrigé

---

numéro de l'oscillogramme	circuit électrique	phénomène physique
1	C3	phénomène 3
2	C2	phénomène 1
3	C1	phénomène 2
4	C2	phénomène 1

phénomène 1 et oscillogramme 2 : la tension aux bornes du condensateur ne présente pas de discontinuité.

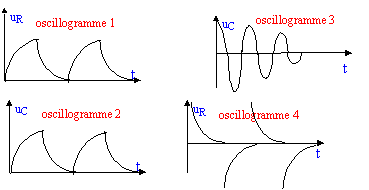
phénomène 3 et oscillogramme 1 : u_R et i sont proportionnelles ; l'image de u_R est celle de i ; retard à l'établissement (ou à la suppression ) du courant dans un circuit inductif.

phénomène 2 et oscillogramme 3 : échange d'énergie entre condensateur et bobine inductive avec amortissement.

phénomène 1 et oscillogramme 4 : le sens du courant de décharge du condensateur (circuit RC) est opposé au sens de l'intensité du courant de charge.

---

le générateur impose sa fréquence au dipôle RLC série : donc oscillations forcées.

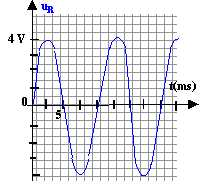
à la résonance d'intensité la fréquence du GBF est égale à la fréquence propre du dipôle RLC. Si la tension aux bornes du dipôle est maintenue constante, alors l'intensité passe par une valeur maximale.

période : 10 ms ( lecture graphe) soit 0,01 s donc fréquence f₀ = 1/0,01 = 100 Hz.

l'ampéremètre indique une intensité efficace : I_eff *1,414 = I_max

I_max = 2* 1,414 = 2,8 mA = 2,8 10^-3 A.

lecture graphe u_{R max} = 4 V

à la résonance d'intensité l'impédance du dipôle RLC série est minimale, égale à la résistance de ce dipôle :

4=R*2,8 10^-3 soit R= 1428 W.