|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Le radon 220 a une demie vie de 54 s tandis que le radon 222 a une demie vie de 3,6 jours. Un appareil proposé aux lycées permet de compter les désintégrations d'une quantité déterminée de radon 222 ou de radon 220.
Données :
La vitesse de la lumière est c = 2,998.108 m.s-1 Le nombre d'Avogadro est N = 6,02.1023 corrigé 86220Rn -->24He + AZX* conservation de la charge : 86=2+Z d'où Z=84 ( polonium) conservation du nombre de nucléons : 220 = 4+A d'où A=216 84216Po * -->84216Po + g. Le temps de demi vie ou période radioactive du radon 220 est très courte (54s) ; or la durée de la mesure des élèves est de l'ordre de 15 s pour le premier groupe et de 60 s pour le second, c'est à dire des durées du même ordre de grandeur que la période radioactive. l'activité de l'échantillon est divisée par deux au bout d'une période: on observe bien une décroissance régulière de l'activité. Le temps de demi vie ou période radioactive du radon 222 est courte (3,6 j) ; la durée de la mesure des élèves est de l'ordre de 15 s pour le premier groupe et de 60 s pour le second, c'est à dire des durées très inférieures à la période radioactive. l'activité de l'échantillon de radon 222 varie donc très peu au cours des mesures. on observe bien une décroissance régulière de l'activité. On observe également le caractère aléatoire des désintégrations : on doit effectué plusieurs mesures puis en faire la moyenne. Enfin le nombre de désintégrations est proportionnel à la durée des mesures. groupe 3 : les mesures sont plus dispersées autour de la moyenne 24,2 désintégrations par seconde groupe 4 : les mesures sont moins dispersées autour de la moyenne 254 désintégrations en 10s. l'activité, nombre de désintégrations par seconde, du radon 222 est 25 Bq au moment du TP. A=l N avec ln2 = l T ( T en seconde : 3,6 j = 3,6*24*3600= 3,1 105 s) l = ln2 / 3,1 105 = 2,23 10-6 s-1. d'où N=A / l = 25 / 2,23 10-6 = 1,12 107 noyaux. Au bout de 24 heures soit 1 j, l'activité initiale est divisée par deux exposant 1/3,6 soit 20,277 = 1,21 A( t=1j) = 25 / 1,21 = 20,7 Bq. perte (défaut) de masse : (3,58603+0,066447-3,65259)10-25 = -1,13 10-29 kg énergie libérée par une désintégration : E=mc² = 1,13 10-29 *(3 108)2 = 1,017 10-12 J 1,017 10-12 / 1,6 10-19 = 6,35 106 eV = 6,35 MeV.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
radon 222 Le radon 222 ( 22286 Rn ) est issu de la désintégration de l'uranium 238 ( 23892 U) contenu dans les rochesterrestres. Plusieurs désintégrations successives de type a ou ß- sont nécessaires pour passer de l.'uranium 238 au radon 222.
corrigé AZX --> 24He + A-4Z-2Y AZX --> -10e + AZ+1Y 23892U --> 22286Rn+ x 24He + y -10e 238 = 222 + 4x d'où x = 4 92 = 86 + 2x - y d'où y = 2 Pour passer de l'uranium 238 au radon 222 il faut 4 désintégrations a et 2 désintégrations ß-. La désintégration d.un noyau radioactif est un phénomène aléatoire. M = 68 ; s = 12 ; m = 1,1 1 Bq est égal à une désintégration par seconde. M est proportionnel au nombre de noyaux qui se sont désintégrés en q s. m est proportionnel au nombre de désintégrations par seconde, m a la dimension d'une activité. 1,1 n.est pas l'activité du radon 222 car : - Une partie de cette lumière sort de la fiole. - l'efficacité du photomultiplicateur est inférieure à 1
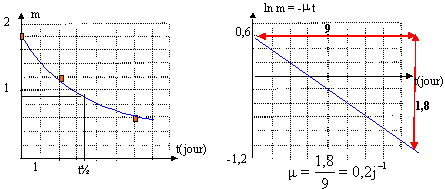
ln m = f(t) sera une droite de coefficient directeur -µ et d'ordonnée à l'origine ln m 0. L'hypothèse est validée m = m 0 e-µt µ = 0,19 jour-1 N = N0 e-lt N : nombre de noyaux à la date t ; N0 : nombre de noyaux à la date initiale l: constante radiaactive en j-1 et t : temps en jours La demi-vie t1/2 est la durée nécessaire pour que la moitié des noyaux présents dans l'échantillon à la date t soit désintégrée à la date t + t1/2 t1/2 = ( ln 2)/l t1/2 = 3,6 jours
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|