|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
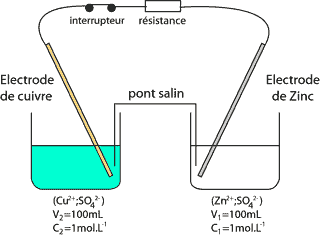
On souhaite réaliser une pile au laboratoire. Pour cela, on dispose d'une lame de zinc et d'une lame de cuivre ainsi que d'un volume V1 = 100 mL d'une solution aqueuse de sulfate de zinc de concentration molaire en soluté apporté C1 = 1,0 mol.L-1 et d'un volume V2 = 100 mL d'une solution aqueuse de sulfate de cuivre de concentration molaire en soluté apporté C2 = 1,0 mol.L-1 et d'un pont salin. L'expérience est réalisée à la température de 25 °C. A cette température, la constante d'équilibre associée à l'équation : Cu2+ + Zn (s)= Cu(s) + Zn2+ ; est K=4,6 1036. La pile ainsi réalisée est placée dans un circuit électrique comportant une résistance et un interrupteur. On ferme ce circuit électrique à l'instant de date t0 = 0 s.
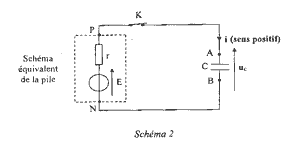
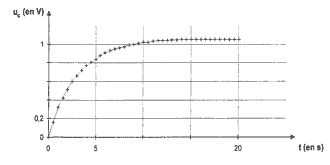
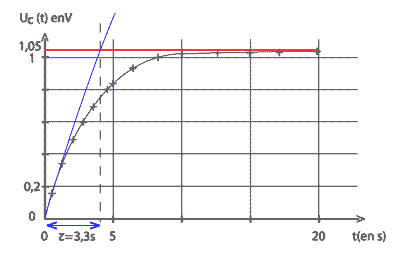
Qr,i = [Zn2+]i/ [Cu2+]i= C1/C2 = 1 valeur inférieure à K : la réaction évolue spontanément dans le sens direct. Zn = Zn2+ + 2e- ; Cu2+ + 2e- = Cu Le zinc est oxydé en Zn2+ (à l'anode). Les électrons libérés par cette oxydation sont disponibles pour le circuit électrique. Donc la lame de Zinc est la borne -. Par conséquent la lame de cuivre est la borne +. Q la quantité d'électricité : D'après le tableau d'avancement les quantités de matière initiales sont en proportions stœchiométriques, donc : C1V1=C2V2 = 0,1 mol soit 0,2 mol d'électrons la charge d'une mole d'électrons vaut : 6,02 1023*1,6 10-19 = 1 F = 96500 C Q= 0,2*96500 = 1,9 104 C. Charge du condensateur : Le condensateur étant chargé complètement, il n'y a plus de charges en mouvement donc i=0. A ce moment là, d'après la loi d'additivé des tensions : E-ri = uC s'écrit E=uC. le graphe donne la valeur de E soit .1,05 V résistance interne de la pile : t = r C, constante de temps du dipôle RC r : résistance (ohm) = te,sion (V) / intensité (A) = V A-1 ; C : capacité (farad) = charge ( coulomb) / tension (V) = intensité * temps / tension = A s V-1 ; r C : V A-1 A s V-1 soit en seconde
r = t / C = 3,3 / 330 10-6 = 104 ohms. Expression de uc(t) : q = Cuc ; i = +dq/dt = CduC/dt( signe + car charge du condensateur ) loi d'additivité des tensions : E= ri + uC = rCduC/dt + uC . E= rC u'C+uC ; t u'C+ uC =E . uc(t) = E(1-e-at) ; dériver par rapport au temps u'C= aEe-at ; report dans l'équation différentielle : t (aEe-at )+ E(1-e-at) =E a t e-at + 1 -e-at = 1 ; a t e-at -e-at = 0 a t = 1 soit a =1/ t ;
|
|||||||||||||||||||||||||||||||||
|
Cet exercice comporte 10 AFFIRMATIONS indépendantes concernant les transformations radioactives. Toute réponse doit être accompagnée de justifications ou de commentaires.A chaque affirmation, vous répondrez donc par VRAI ou FAUX, en justifiant votre choix à l'aide de définitions, de calculs, d'équations de réactions nucléaires,... A la fin du XIXème siècle, Pierre et Marie Curie découvrent deux éléments chimiques : le polonium puis le radium. Marie Curie obtient en 1903 le prix Nobel de physique et, en 1911, celui de chimie. Le radium 22688Ra se désintègre spontanément en émettant une particule a . Le noyau fils est un isotope du radon (Rn). Le radon est un gaz dans les conditions ordinaires de température et de pression. Le 22688Ra est radioactif b-.
Données : L'activité A d'un échantillon radioactif est le nombre de désintégrations qu'il produit par secondes. A un instant de date t, A est proportionnelle au nombre N(t) de noyaux radioactifs contenus dans l'échantillon à cet instant et à la constante de radioactivité l. La particule a est un noyau d'hélium noté 42He.Célérité de la lumière dans le vide c = 2,998 10 8m.s-1 1 eV = 1,6 10-19 J ; 1 an = 3,156 107 s ; Constante d'Avogadro NA= 6,02 1023 mol-1.
84 est le numéro atomique = nombre de protons 208 est le numéro de masse = nombre de nucléons (protons + neutrons). 2. FAUX : la masse d'un noyau est inférieure à la somme des masses des nucléons : la différence s'appelle défaut de masse. 3. VRAI : "le radium se désintègre spontanément en émettant une particule a (42He), le noyau fils étant un isotope du radon". conservation de la charge électrique : 88 = 2+86. conservation du nombre de nucléons : 226 = 4+222. 4. FAUX : radium et radon ne sont pas isotopes : leurs numéros atomiques sont différents. 5. FAUX : le radium étant radioactif b- l'équation de désintégration est : 22688Ra --> 0-1e + AZX avec 88 = -1+Z Soit Z = 89, qui n'est pas le numéro atomique du Francium, mais celui de l'Actinium. 6. VRAI : d'après la loi de décroissance radioactive, N = N0e-lt. Or, la demi-vie t½ du radon est définie par : l t½=ln2 Comme t = 3 t ½ le pourcentage de noyaux de radon restant au bout de t = 11,4 jours est donc : N0 / 23 = N0 / 8 = 0,125 N0 ; soit 12,5% 7. FAUX : S'il y a émission de 2 particules 42He et de 3 électrons, le noyau obtenu est le proactinium 230. 23892U --> 42He + 23490Th 23490Th-> 42He + 23088Ra 23088Ra --> 3 0-1e +23091Pa 8. FAUX : l'activité du radium 226 est le nombre de désintégrations par seconde : A = 6,0 * 105 Bq. Le nombre de noyaux désintégrés en 1 minute est donc égal à : 6,0 * 105 * 60= 3,6 107. 9. FAUX : l'énergie libérée par la réaction est définie par : Dm = (3,752 438 10-25 - 0,066 4465 10-25 - 3,685 904 10-25) =8,75 10-30 kg E=Dm c² = 8,75 10-30* 2,9982 x 1016= 7,865 10-13 J 7,865 10-13 / 1,6 10-19 = 4,909 MeV. 10. VRAI : pour 1m3 de radon, A = 3,75 103 Bq Or A = l N ; N= A / l =3,75 103 /2,1 10-6 = 1,786 109 noyaux quantité de matière en radon, dans 1m3, responsable de l'activité : 1,786 109/ 6,02 1023 = 2,97 10-15 mol
|
||||||||||||||||||||||||||||||||||
|