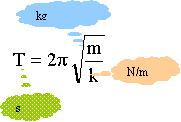|
avec calculatrice En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
A- étude d'un séisme : Lors d'un séisme, la Terre est mise en mouvement par des ondes de différentes natures qui occasionnent des secousses plus ou moins violentes et destructrices en surface. On distingue : - Les ondes P, les plus rapides, se propageant dans les solides et dans les liquides. - Les ondes S, moins rapides, ne se propageant que dans les solides. Les schémas ci-dessous modélisent la progression des ondes sismiques dans une couche de terre : 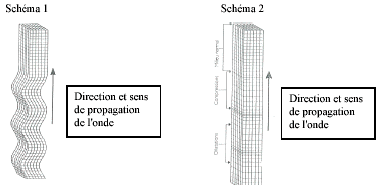
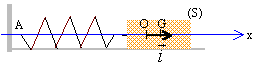
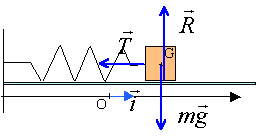
B- Oscillateur mécanique susceptible d'être excité par une onde sismique logitudinale. L'onde sismique longitudinale est modélisée par une onde sinusoïdale d'amplitude As et de période Ts qui se propage suivant une direction horizontale. Cette onde peut agir sur un oscillateur mécanique horizontal et provoque des oscillations horizontales d'amplitude A et de période T. On étudie le comportement de l'oscillateur horizontal dans différentes situations.
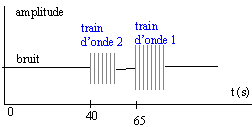
Le train A correspond aux ondes les plus rapides : ondes P; le train B aux ondes les moins rapides, ondes S. Le séisme s'est déclenché à l'épicentre 40 s plus tôt soit 8 h 14 min 50 s. distace épicentre- EUREKA = 10*40 = 400 km. les ondes S
parcourent 400 km en 65 s soit : v= 400 / 65 = 6,1 km/s.
à une date t, il
faut ajouter la tension du ressort :
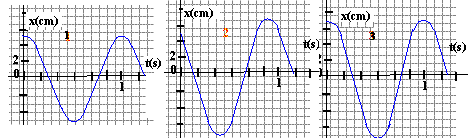
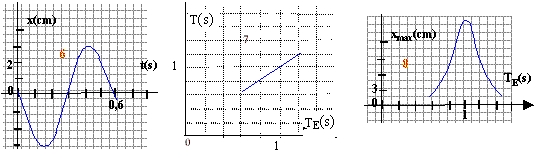
écrire la 2 ème loi de Newton sur l'axe horizontal : -kx = m x" soit x"+ k/m x=0 ou encore x" +w0² x=0 (1) pulsation w0 = 2p / T0. xmax : amplitude (m ) ; T0 : période propre (s) ; j0 phase à la date t=0 ( rad) ; x : élongation (m) ; t : temps (s) m=0,25 kg; k = 10 N/m ; T0 = 6,28 ( 0,25/10) ½ = 0,993 s en accord avec la valeur lue sur les graphes expérience 3 : amplitude xmax=7 cm ; vitesse initiale nulle ( à t=0 la tangente à la courbe est horizontale). xmax 1 =5 cm ; xmax 2 =7 cm ; xmax 3 =7 cm ; La période est identique ( lecture sur les 3 graphes), donc indépendante des conditions initiales. L'amplitude dépend de la vitesse initiale ( graphes 1 et 2 (élongation initiale identique)) et de l'élongation initiale ( graphes1 et 3 (vitesse initiale identique)) expériences 4 et 5 : calcul de la période T0 4 = 6,28 ( 0,5/10) ½ = 0,444 s ; T0 5 = 6,28 ( 0,25/7) ½ = 1,19 s ; L'amplitude des oscillations ne dépend pas de la période de l'oscillateur.
expérience 6 : T=TE=0,6 s et xmax= 3cm différent de AE. graphe 7 : T=f(TE) est une droite de coefficient directeur égal à 1 : donc T=TE; l'excitateur impose sa fréquence à l'oscillateur. graphe 8 : phénomène de résonance d'intensité ( xmax passe par une valeur extrème); à la résonance T0=TE. la direction de propagation de l'onde longitudinale et l'axe de l'oscillateur doivent être parallèlle. l'onde sismique ( l'excitateur) impose sa période Ts à l'oscillateur ( oscillations forcées). si Ts= T0, xmax passe par une valeur extrème, bien supérieure à As.( résonance) si Tsdiffére de T0, xmax passe par une valeur qui dépend de TE, valeur qui peut être supérieure à As ou inférieure ( graphe 8)
|
|||||
|