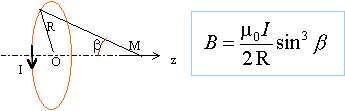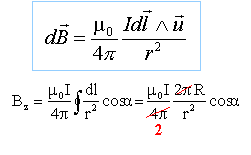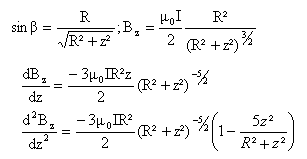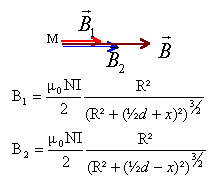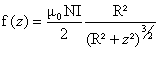Aurélie sept 2001
les courants sources de champs magnétiques

Capes interne 94 exercice suivant (solénoïde)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

bobines de Helmoltz.

 

  1. On considère une spire circulaire de rayon R parcourue par un courant d'intensité I. En utilisant les symétries que peut-on dire de la direction du champ magnétique crée par cette spire en un point de son axe? En utilisant de Biot et Savart montrer que le champ magnétique crée en un point M de son axe par une spire circulaire de rayon R parcourue par un courant d'intensité I a pour expression :

    - Compléter la figure en indiquant le sens de B.
    - Tracer qualitativement la courbe donnant la variation de B en fonction de la distance z du point M à O. Vérifier que la courbe présente un point d'inflexion pour z= ½ R
    - Donner la valeur du rapport B(z=½R) / B (z=0)
    - application numérique : N = 130 spires ; R= 15 cm ; I=1,7 A . Calculer B au centre de la bobine et comparer cette valeur à la composante horizontale du champ magnétique terrestre BT= 2 10-5 T

  2. On considère un dispositif constitué de 2 bobines plates identiques à celle étudiée ci-dessus, de même rayon R, de même axe et comptant N spires. Chacune de ces bobines est parcourue par un courant d'intensité constante I et de même sens. La distance entre les centres O1 et O2 des bobines vaut d. On appelle O le milieu de O1O2 et x la distance d'un point M sur l'axe au point O. On se propose de montrer que pour une certaine valeur de d que l'on exprimera en fonction de R, le champ magnétique varie très peu sur l'axe au voisinage du point O: le dispositif est alors appelé bobines de Helmoltz. Montrer que le champ magnétique au point M peut se mettre sous la forme B(x) = f( z=½d+x) + f(z=½d-x) où f est une fonction que l'on définira.
    - en effectuant un développement limité pour x petit, faisant intervenir les dérivées 1ère, seconde et du 3ème ordre de la fonction f(x) montrer que pour une certaine valeur de d, que l'on exprimera en fonction de R, le champ magnétique se met sous la forme : B(x) = 2f(½d)+0x3.
    - A.N: avec les valeurs numériques précédentes, calculer dans cette configuration le champ magnétique en O, milieu de O1O2 et celle du champ magnétique au centre de l'une des bobines. Conclure.

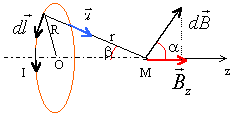
Tout plan passant par Oz est un plan d'antisymétrie du système. En conséquence le champ magnétique est porté par l'axe Oz

On applique la relation de Biot et Savart :

cos a = sin b. angles complémentaires

r = R / sin b.

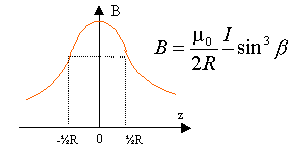
La courbe B(z) présente un point d'inflexion en z= ½R si la dérivée seconde s'annule en ce point.

ceytte dérivée seconde s'annule pour z =½R et z = - ½R; la courbe présente deux points d'inflexion.

B(z=0) = m0I / (2R) et B( z=½R) = 4m0I / (53/2R)

B(z=½R) / B(z=0) = 0,715.

A.N : B(z=0) = m0N I / (2R) = 4p10-7 * 130*1,7 /(2*0,15) = 0,926 mT.

cette valeur est 46 fois plus grande que la valeur de la composante horizontale du champ magnétique terrestre.

bobines de Helmoltz :

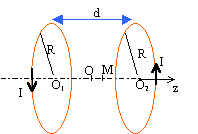
Les champs crées par chaque bobine ont la même direction et le même sens; le champ résultant est la somme vectorielle des champs crées par chaque bobine.

B peut se mettre sous la forme :

B(x) = f( z=½d+x) + f(z=½d-x) où f est :

On effectue le développement limité pour x petit:

f(½d+z)= f(½d) + xf '(½d) + ½x² f ''(½d) + x3/6 f '''(½d)+ 0 x3.

f(½d-z)= f(½d) - xf '(½d) + ½x² f ''(½d) - x3/6 f '''(½d)+ 0 x3.

la somme donne : B(x) = 2 f(½d) + x² f ''(½d)+ 0 x3.

si d=R, alors f ''(½d) = 0 car la dérivée seconde d²B / dz² est nulle pour z=½R

d'où B(x) = 2 f(½d) + 0 x3.

A.N : champ au point O : 1,32 mT; champ en O1 : 1,25 mT

l'écart relatif est voisin de 5% entre le centre des deux bobines et l'une ou l'autre des deux bobines.

On peut considérer que le champ magnétique est uniforme sur l'axe, entre les deux bobines de Helmholtz.

retour - menu