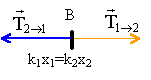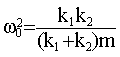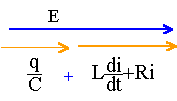kiné Lariboisière 2000

Aurélie déc 2000

	d'après concours kiné E.F.O.M 2000
1 oscillateur mécanique	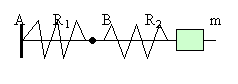Deux ressorts R₁ et R₂ de constante de raideur K₁ et K₂ sont reliés entre eux par un crochet B, de masse négligeable. La masse m peut glisser sans frottement sur une tige horizontale. On note x₁ et x₂ les élongations respectives à un instant t des 2 ressorts. Chaque élongation est comptée à partir de la position à vide du ressort correspondant. En appliquant le théorème du centre d'inertie au crochet B, établir la relation entre x₁ et x₂. Exprimer x₁ en fonction de k₁, k₂ et de l'élongation totale x des 2 ressorts (avec x = x₁+x₂) .De même exprimer x₂ en fonction de k₁, k₂ et x. Exprimer la somme des énergies potentielles élastiques des 2 ressorts en fonction de k₁, k₂ et x. En utilisant la relation traduisant la conservation de l'énergie mécanique de ce système, établir l'équation différentielle de cet oscillateur (R₁, R₂ ,m). Exprimer sa pulsation propre w₀ en fonction de k₁, k₂ ,m. corrigé
	principe des actions mutuelles en B x = x₁+x₂ et x₂ = k₁ x₁ / k₂d'où : x₁= x-k₁ x₁ / k₂ x₁ = k₂ x / (k₁+k₂) de même x₂ = k₁ x / (k₁+k₂) énegie potentielle élastique d'un ressort : 0,5 k x². 0,5 k₁ x₁² + 0,5 k₂ x₂². remplacer x₁ et x₂ par les expressions ci dessus. mettre k₁k₂ / (k₁+k₂)² en facteur commun. Ep =0,5 k₁k₂ / (k₁+k₂) x² énergie mécanique = énergie cinétique + énergie potentielle. écrire la conservation de l'énergie mécanique du système constitué par les 2 ressorts et la masse m. Em = 0,5 mv²+ 0,5 k₁k₂ / (k₁+k₂) x² = constante dériver par rapport au temps ( u²)' = 2uu' 0,5 m (2v'v) +0,5 k₁k₂ / (k₁+k₂) (2xx') = 0 remarquer que x' =v et x"=v' m x" x' + k₁k₂ / (k₁+k₂) x x' =0 diviser par x' chaque therme : mx" + k₁k₂ / (k₁+k₂) x =0 cette expression liant la dérivée seconde x" et la fonction x est l'équation différentielle cherchée.
2 déviation des électrons	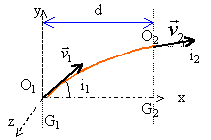On négligera le poids des électrons devant les autres forces. Une source S, dont le potentiel électrique V_S est nul, émet des électrons avec une vitesse pratiquement nulle. Ces électrons arrivent sur une grille G₁ au potentiel V₁. Exprimer la vitesse v₁ d'un électron passant par un trou de G₁, en fonction de la masse de l'électron m ,de V₁ et de la charge élémentaire e. Que se passerait-il si V₁ était négatif ? Au delà de G₁ à la distance d, est disposée une seconde grille G₂, parallèle à G₁, de potentiel V₂. Déterminer les expressions en fonction du temps des coordonnées du vecteur vitesse d'un électron allant de O₁ à O₂. Un électron passe par un trou de G₂ à la vitesse v₂. Exprimer v₂ en fonction de e, m, et V₂. Déterminer sin i₂ en fonction de v₁, i₁, et v₂. Que se passerait-il si V₂ était négatif ? Etablir la relation entre i₁, i₂, V₁et V₂. corrigé
	écrire le théorème de l'énergie cinétique entre la source et le point O₁. la vitesse initiale est nulle. Le potentiel de la source S est nulle. l'électron placé dans un champ électrique est soumis à une force électrique . Le travail de cette force est : -e( V_S -V₁). 0,5 mv₁² -0 = eV₁. v₁²=2eV₁/ m. Si V₁ était négatif, le travail de la force électrique serait résistant et les électrons n'atteindraient jamais la grille G₁. 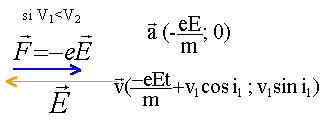entre G₁ et G₂ seule la force électrique intervient. Seule la composante de la vitesse, dans la direction de la force, varie. L'ordonnée du vecteur vitesse reste donc constante. soit v₁ sin i₁ = v₂ sin i₂.(1) écrire le théorème de l'énergie cinétique entre G₁ et G₂. la force électrique effectue le travail : -e(V₁-V₂) si ( V₁-V₂) est négatif, les électrons sont déviés et accélérés entre les 2 grilles. si ( V₁-V₂) est positif, les électrons sont déviés et freiné entre les 2 grilles : il se peut que la seconde grille ne soit pas atteinte. 0,5 mv₂² -0,5 mv₁² = -e(V₁-V₂) avec 0,5 mv₁² = eV₁. 0,5 mv₂² -eV₁= -eV₁+eV₂. v₂² =2eV₂ / m. remplacer les vitesses par leurs expressions en fonction des potentiels électriques dans (1).
3 charge oscillante	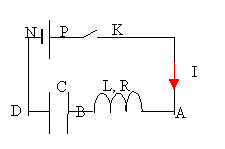Un générateur de tension continue maintient entre ces bornes une tension U_PN constante, égale à sa f.é.m E=12V. Le condensateur DB de capacité C=10mF est initialement déchargé. La bobine a une auto-inductance L=0,1 H , sa résistance est R. On néglige la résistance R de la bobine. On abaisse l'interrupteur K à la date t=0. établir l'équation différentielle reliant la charge algébrique q=q_B du condensateur à L, C, et E. On se propose de déterminer la fonction q(t) en faisant un changement de variable. Dans l'équation différentielle précédente faire le changement de variable Q= q - EC. Déterminer alors la fonction Q(t). A la date t=0 on a : q₀=0 et i₀=0 . En déduire la fonction q(t) et la représenter graphiquement. En fait la bobine a une résistance R, assez faible, qui amortit les oscillations. Dessiner l'allure de la courbe représentant q(t). Déterminer la limite vers laquelle tend : La charge du condensateur L'intensité du courant i L'énergie de l'oscillateur RLC corrigé
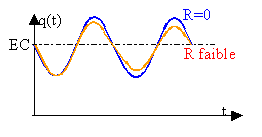
	écrire que la tension au borne du générateur est égale à la somme des tensions aux bornes du condensateur et de la bobine . remarquer que : i=q' ; di/dt=i' = q" q / C + L q''+Rq' = E si R est négligé le therme Rq' disparaît. diviser tous les thermes par l'inductance L : q" +1/ (LC) q =E / L ( éq. différentielle). Q=q-EC ; Q"=q" Q" + 1/(LC) Q + E/L = E/L soit Q" + 1/(LC) Q =0 Q(t) = A cos(wt+j) soit q(t) =A cos(wt+j) +EC pulsation w= racine carrée (1 /(LC))= rac carrée (1/(0,1* 10^-5))=10³ rad s^-1. A et j sont des constantes déterminées d'après les conditions initiales. à t=0 intensité nulle : dériver q par rapport au temps i = q' = 0 = -1000A sin(wt+j) = -1000A sinj. --> j=pou j=0 à t=0 charge nulle d'où : 0 = A cosp+EC soit A=EC q(t) =EC( 1+cos(wt+p)) ou q(t) =EC( 1-cos(wt)). La bobine s'oppose ( introduit un retard ) à la charge du condensateur. Au bout d'un temps assez long la charge du condensateur tend vers la valeur CE =1,2 10^-4 C. Lorsque le condensateur est chargé, la tension à ses bornes est égale à E. L'intensité du courant est alors nulle. La tension aux bornes de la bobine est nulle. L'énergie est stockée par le condensateur. 0,5 Q² / C =0,5 CE² = 0,5 10^-5* 12² = 7,2 10^-4 J retour - menu