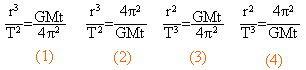Aurélie sept 2001
Gravitation - satellite terrestre

d'après concours GEIPI 2000 exercice suivant

 

 

  1. La force de gravitation s'exerçant entre la terre et le soleil vaut F=3,5 1022 N. Connaissant la constante de gravitation G=6,67 10-11 SI, la masse de la terre Mt =6 1024 kg et la distance terre soleil d=1,5 108 km, exprimer en fonction des données la masse Ms du soleil puis calculer sa valeur numérique.
  2. Un satellite assimilé à un point matériel de masse m décrit d'un mouvement uniforme dans le champ de gravitation de la terre une orbite circulaire à l'altitude h= 400 km. L 'orbite est située dans le plan équatorial de la terre et le rayon terestre a pour valeur R=6400 km.
    - Déterminer dans le repère géocentrique la vitesse V du satellite en fonction de G, Mt et r ( r étant le rayon de la trajectoire). Calculer la valeur numérique de V.
    -Déterminer dans le même repère, les expressions littérales et les valeurs numériques de la période T et de la vitesse angulaire w du satellite.
  3. Le mouvement de ce satellite obéit à la troisième loi de Képler qui a pour expression ( choisir l'expression correcte)
  4. Déterminer en fonction de Mt, G, R et T=86400s (période de révolution de la terre sur son axe), l'altitude h0 à laquelle un satellite en orbite circulaire équatoriale autour de la terre doit évoluer pour qu'il soit géostationnaire.Calculer la valeur numérique de h0.
corrigé
force de gravitation proportionnelle aux masses et inversement proportionnelle au carré de la distance

F = G Mt Ms / d² masse en kg et distance en m.

d = 1,5 1011 m

Ms = F d² / ( G Mt) = 3,5 1022 * 10,5² 1022 / (6,67 10-11*6 1024) = 1,96 1030 kg.

Le satellite est soumis uniquement à la force de gravitation centripète F=G Mt m / r²

le mouvement est circulaire uniforme.

l'accélération normale est égale à : aN= V² / r

la relation fondamentale de la dynamique ( 2ème loi de Newton) projetée sur l'axe n de la base de frenet donne :

V² / r = G Mt / r²

d'où V² = G Mt / r avec r = (6400+400) 103 = 6,8 106 mètres

V² = 6,67 10-11 * 6 1024 / 6,8 106 = 5,88 107.

V=7668 m/s.

la période est la durée nécessaire pour parcourir une circonférence à la vitesse V

2pr = V T

4p²r² = V² T²

remplacer V² par l'expression ci dessus.

4p²r² =G Mt T² / r

soit T² = 4 p² r3 / (G Mt) ( 3ème loi de Kepler)

l'expression (1) est correcte.

T² = 4*3,14² * (6,8 106)3 / (6,67 10-11*6 1024) d'où T= 5558 s.

la vitesse angulaire est égale à : w = 2p / T = 6,28 / 5558 = 1,13 10-3 rad/s.

r3 = T² G Mt / (4 p²) d'après la 3ème loi de Képler.

avec r = R +h0.

r3 = (8,64 104 )² *6,67 10-11*61024 /( 4*3,14²) = 75,75 1021 m3.

r = 4,237 107 m = 42370 km

h0= 42300-6400= 35970 km.

retour - menu