devoirs terminale

Aurélie février 2001

	concours kiné Strasbourg 2000 physique exercices suivants quelle (s) est (sont) la (les ) affirmation(s) exacte(s) ?
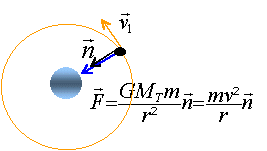
1 objet laché d'un train	Données pour les 3 premiers exercices: m =500g ; V=108 km/h ; F = 4 N; h =2m. Un train roule à la vitesse constante V sur une voie horizontale rectiligne. Un voyageur lâche par la fenêtre d'un point situé à la hauteur h au dessus du sol un objet de masse m, assimilable à un point matériel. Le vecteur vitesse de l'objet par rapport au sol est à l'instant du lâcher : De direction horizontale, dans le sens du mouvement du train De direction verticale, dans le sens inverse du mouvement du train Nul De direction verticale de haut en bas. corrigé
	au moment du lâcher de l'objet, celui ci a la même vitesse que le train: même norme : 108 /3,6 = 30 m /s. même direction horizontale même sens que le mouvement du train affirmation 1 exacte, les autres sont fausses.
2 étude de la chute	On veut étudier le mouvement de l'objet lors de sa chute. Celui ci a été lâché à la date t=0 au point D , d'altitude h au dessus du sol. On représente l'action de l'air sur l'objet par une force F constante colinéaire au vecteur vitesse du train et de sens contraire à celle ci. On étudie le mouvement dans un repère terrestre. Le mouvement de l'objet suivant l'axe Ox est rectiligne uniforme. Le mouvement de l'objet suivant l'axe Oz est rectiligne uniformément varié. La trajectoire de l'objet est rectiligne. La trajectoire de l'objet est parabolique corrigé
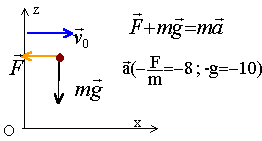
	le mouvement n'est pas rectiligne uniforme suivant l'axe Ox car la somme vectorielle des forces n'est pas nulle suivant Ox. le mouvement est uniformément varié sur l''axe Ox et sur l'axe Oz. vecteur vitesse : v_x= -8t+30 et v_y = -10t. vecteur position : x= -4t²+30t y= -5t²+2 la trajectoire n'est ni une droite, ni un arc de parabole (équation du type y=ax²+bx+c) affirmation 2 exacte, les autres sont fausses.
3 point d'impact	L'objet touche la voie ferrée en un point I La distance OI est voisine de 17 m. La distance OI est voisine de 15 m. La position du point de la fenêtre où l'objet a été lâché est au même instant à la verticale du point d'impact I.. Le point d'impact I dépend de la résistance de l'air.. corrigé
	l'ordonnée du point d'impact est égale à zéro d'où la valeut du temps correspondant : -5t²+2=0 t²= 0,4 et t = 0,632 s. remplacer t par 0,632 s dans l'expression de l'abscisse x: x=-40,632²+300,632 = 17,36 m. pendant 0,636 s le train parcourt à vitesse constante : 0,63630=18,96 m. le point d'impact n'est pas à la verticale de la fenètre. Dans l'expression de l'abscisse OI, la résistance de l'air intervient. affirmations 1 et 4 exactes, les autres sont fausses*.
4 satellite	Un satellite artificiel S₁ de masse m₁ est assimilable à un point matériel. Dans un repère géocentrique, supposé galiléen, son orbite est assimilée à un cercle de rayon r et de même centre O que la terre. Le satellite n'est soumis qu'à l'attraction terrestre. Un véhicule spatial S₂ de masse m₂ est sur la même orbite que S₁, ses moteurs étant éteints. Les astronautes de S₂ cherchent à rejoindre S₁ en restant sur la même orbite de rayon r. Pour cela ils allument un moteur auxiliaire faisant passer leur vitesse de v₀ à la valeur v₂. 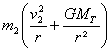La vitesse du satellite est telle que v² r =GM_T. La vitesse du véhicule spatial est égale à celle du satellite. Alors que le véhicule spatial S₂ se dirige vers S₁ sur orbite de rayon r, à la vitesse v₂, le moteur exerce une force tangentielle F dans le sens du mouvement. L'expression de cette force F est corrigé
	Le satellite n'est soumis qu'à la force de gravitation centripète (dirigée vers le centre de la terre) On utilise le repère de Frenet : suivant l'axe n, la seconde loi de Newton s'écrit: cette vitesse est indépendante de la masse : deux satellites situés sur la même orbite ont la même vitesse. Le véhicule reste sur la même orbite que le satellite lors de l'approche: la force f exercée par les moteurs est tangentielle. L'expression de cette force n'est pas celle proposée, cette expression correspond à une force centripète. affirmations 1 , 2 et 3 exactes, l'affirmation 4 est fausse.
5 pendule dans un véhicule descendant une côte	Déplacement sans frottement et sans vitesse initiale. 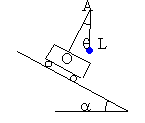L'angle q est égal à l'angle a. Le pendule est à gauche du support OA. l'angle q est nul la tension du fil a pour valeur : T=mg cos a / cosq . corrigé
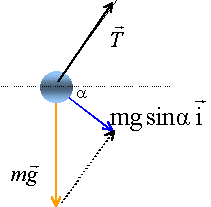
	l'accélération du véhicule est égale à gsina. La somme vectorielle des forces (poids et tension) appliquée au pendule est donc colinéaire au plan incliné. Cela entraîne q=0. la tension du fil est mg cos a . L'expression de la tension proposée est exacte car cosq=cos0=1 affirmations 3 et 4 exactes, affirmations 1 et 2 fausses.
6 chute et rotation de la terre	Vous êtes à Kuala Lumpur quasiment situé sur l'équateur.. Un jeune homme se penche par la fenêtre de la plus haute tour du monde : orienté vers le nord, il lâche une bille d'acier d'un point B. La fenêtre est située à 405 m au dessus du sol. On rappelle que la terre tourne de l'ouest vers l'Est et on admet qu'elle effectue un tour en T=9 10⁴ secondes. On néglige les frottements. Le point d'impact de la bille est à 4 km du pied de la tour vers l'ouest car la terre a tourné. Le point d'impact est au pied de la tour (verticale de B). Le point d'impact est à 25 cm à l'ouest du pied de la tour (verticale de B). Le point d'impact est à 25 cm à l'est du pied de la tour (verticale de B) corrigé
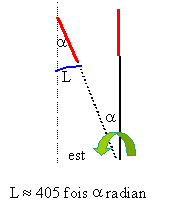
	En tenant compte du sens de la rotation de la terre, le point d'impact est à l'est. Durée de la chute en négligeant les frottements: 405=4,9 t² d'où t =9,1 s. angle décrit par la terre en 9,1 s : 2p 9,1 / 9 10⁴ =6,35 10^-4 radian puis 4056,35 10^-4 = 0,25 m. affirmation 4 exacte, affirmations 1, 2 et 3 fausses.
7 le train démarre	Sur le quai d'une gare une voyageuse en retard court pour essayer de prendre son train à une vitesse constante v=8 m/s. Le train démarre alors qu'elle est encore à une distance d du dernier wagon. L'accélération constante du train est 0,5 m/s². La voyageuse n'atteindra jamais le train si d est supérieure à 64 m. Si d=100 m la voyageuse s'approchera à 40 m du dernier wagon. Si d=60 m la voyageuse mettra 20 s pour atteindre le dernier wagon. Si d=28 m la voyageuse mettra 4 s pour atteindre le dernier wagon. corrigé
	origine des distances le voyageur à t=0 ; le dernier wagon du train est devant lui à la distance d. distance parcourue par le voyageur (mouvement rectiligne uniforme) d₁=8t ; abscisse du voyageur x₁=8t . distance parcourue par le train d₂=0,25 t² ; abscisse du dernier wagon : x₂ = 0,25 t²+d le voyageur rattrappe le train, écrire x₁=x₂. 0,25 t²+d=8t ou 0,25 t²-8t+d=0 D=b²-4ac =64-d si la distance est supérieure à 64 m, le discriminant est nul, il n'y a pas de solution : le train n'est pas rattrappé. d=60 m : D= 4 et t = 12 s pour atteindre le dernier wagon d=28 m : D= 36 et t = 4 s pour atteindre le dernier wagon la distance est de 100m , x₂-x₁ est minimale lorsque sa dérivée est nulle : (0,25t²+100-8t)'=0,5t-8 d'où t=16s le voyageur a parcouru : 816 = 128 m le train se trouve à l'abscisse : 100+0,25 16² = 164 m distance entre le voyageur et le dernier wagon: 36 m. affirmations 1 et 4 exactes, affirmations 2 et 3 fausses.
8 plan incliné et contre poids	Les forces de frottements exercées sur le solide de masse m₁ sont assimilées à une force colinéaire mais de sens contraire à la vitesse. On communique une vitesse initiale v₀ au solide de masse m₁, parallèle au plan vers le haut. 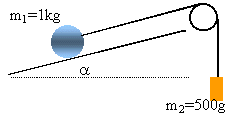Si v₀=0 alors le système reste en équilibre Si v₀ non nulle et pas de frottements alors le système a un mouvement uniforme. v₀=0,5 m/s et pas de frottement, la tension du fil vaut 5 N. v₀=0,5 m/s et frottement =3N, la tension du fil vaut 8 N. corrigé
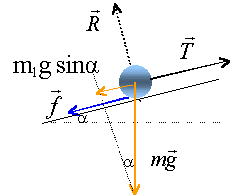
	vitessev v₀ nulle: s'il y a équilibre la somme vectorielle des forces appliquées à la masse m₁ doit être nulle. de plus T=m₂g =0,59,8 = 4,9 N m₁gsina = 19,8sin30 = 4,9N si les frottements sont nuls, il y a équilibre. si les frottements ne sont pas nuls, la somme vectorielle des forces appliquées à m₁ n'est pas nulle et il n'y a pas d'équilibre. v₀ non nulle et frottement nul* : d'après le développement précédent la somme vectorielle des forces appliquées à m₁ est nulle. Le principe d'inertie nous dit que le mouvement est rectiligne uniforme. v₀ =0,5 m/s et frottement nul : mouvement rectiligne uniforme T=m₂g =4,9 N voisin de 5 N. v₀ =0,5 m/s et frottementf=3N : somme vectorielle des forces appliquées à m₁ = m₁ fois accélération projection sur un axe parallèlle au plan vers le haut : -m₁gsina +T-f = m₁a -4,9-3 +T = a (1) lappliquons la seconde loi de Newton au solide m₂: (axe vertical descendant) m₂g-T=m₂a 4,9 -T=0,5 a d'où a= 9,8 -2T repport dans (1). -7,9 +T = 9,8 -2T T= 5,9 N. affirmations 2 et 3 exactes, affirmations 1 et 4 fausses. retour - menu