|
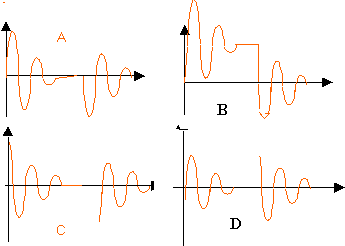
quelle (s) est (sont) la (les ) affirmation(s) exacte(s) ?
|
|
|
circuit RLC tension intensité |
Un circuit RLC est alimenté par un générateur délivrant une tension crénaux. 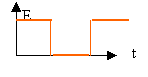
corrigé |
|
La bobine inductive stocke de l'énergie, puis déstocke celle ci et introduit un retard à la charge du condensateur. Lorsque le condensateur est chargé, l'intensité du courant est nulle, la tension aux bornes du condensateur vaut E, la tension aux bornes de la bobine est nulle. B correspond à la tension aux bornes du condensateur. A partir de t=0, (condensateur non chargé) l'intensité augmente à partir de zéro, puis s'annule lorsque le condensateur est chargé. à t=0, tension nulle aux bornes du condensateur, intensité nulle donc Ri=0 (tension aux bornes du résistor). Dipoles en série, alors la tension E est appliquée aux bornes de la bobine. C : tension aux bornes de la bobine la tension crénaux vaut 0 : le condensateur se décharge à travers la bobine et la résistance R. La tension aux bornes du condensateur va tendre vers 0, après quelques échanges d'énergie avec la bobine. L'intensité du courant a, au début de la décharge, le sens contraire à celui du début de la charge. Au début de la décharge, la bobine n'a pas eu le temps de stockée de l'énergie, le condensateur n'a pas eu le temps de se décharger, l'intensité vaut donc zéro. La tension aux bornes de la bobine vaut -E au début de la décharge. A : intensité
|
|
|
largeur de la bande passante |
Pour doubler la bande passante d'un circuit RLC de fréquence f0.
corrigé |
|
oscillations forcées : bande passante Df = SR / (2pL) avec LCw²=1 soit Df = SRCw²/(2p) pour doubler la bande passante on peut ou bien doubler R diviser par deux l'inductance L multiplier par deux la capacité C diminuer L et augmenter C affirmations 1 et 3 exactes, les autres sont fausses. |
|
|
tension aux bornes du condensateur |
Un circuit constitué d'un condensateur de capacité C=10 mF et d'un dipôle ohmique de résistance R=50 W est alimenté par un générateur idéal de tension tel que la tension aux bornes du conducteur ohmique soit u(t) = 5 cos(5000t). La tension aux bornes du condensateur est donnée par :
corrigé |
|
aux bornes du résistor, tension et intensité sont proportionnelles intensité : i(t) = 5/50 cos(5000t) =0,1 cos(5000t) tension aux bornes du condensateur : u(t) = q(t) / C
u(t)= 0,1 / 5000 10-5sin(5000t) = 2 sin(5000t) affirmation 1 exacte, les autres sont fausses. |
|
|
ouverture d'un circuit inductif |
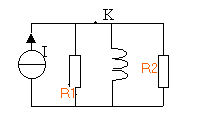 Soit le circuit ci contre alimenté à l'aide d'un générateur de courant .L=60 mH; R1=R2=1 kW; I=1A.
|
|
la bobine stocke de l'énergie : 0,5 Li² tension aux bornes de la bobine : u=Ldi/dt or i est constant, donc u =0 la tension est nulle aux bornes de chaque résistor monté en dérivation avec la bobine. l'intensité du courant est nulle dans chaque résistor intensité du courant dans la bobine I=1A énergie stockée : 0,5*0,06*1² = 0,03 J interrupteur ouvert : la bobine libère 0,03 J dans le résistor R2. En conséquence,aucune étincelle n'apparaît aux bornes de l'interrupteur. l'intensité ne change pas de sens après l'ouverture de K. loi d'Ohm : Ldi/dt +R2i=0 i' +R2 / L i=0 i = A exp(-R2/L t) lorsque la bobine a libérée son énergie l'intensité devient nulle à t=0 (ouverture de K) : i0 = 1A i = 1 exp(-R2/L t) affirmation 1 exacte, l'affirmations 2, 3 et 4 fausses. |
|
|
décharge d'un condensateur dans deux condensateurs |
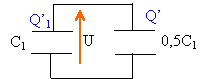
On réalise le montage suivant : à l'instant initial le condensateur C1 est chargé sous une tension U1. On ferme l'interrupteur K et on attend l'équilibre électrique. Les 3 condensateurs sont identiques. La tension U2 aux bornes du condensateur C2 vaut : 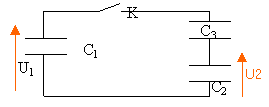
corrigé |
|
Qinitiale= U1 C1 Les deux condensateurs C2 et C3 identiques, en série, peuvent être remplacés par un condensateur unique de capacité C= 0,5 C1.
U tension aux bornes de C1 ou aux bornes de C Q'1 : charge finale de C1 et Q' charge finale de C. Qinitiale =Q'1+Q U1 C1 = UC1 + U * 0,5C1 = 1,5 U* C1. soit U=U1/ 1,5 et U2 = U1/3 affirmation 4 exacte, affirmations 1, 2 et 3 fausses. |
|
|
tranformateur |
Transformateur idéal à vide : tension aux bornes du primaire U1=22V; N1=1000 spires. Le secondaire est constitué de 2000 spires.
corrigé |
|
rapport de transformation : U2/U1 = N2/N1=2 U2 = 2*22 = 44V affirmations 1 et 3 exactes, affirmations 2 et 4 fausses. |