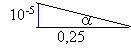| |
le microscope Nlle calédonie 99 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||||||||||||||||||||||||||||||||||
| |
|
||||||||||||||||||||||||||||||||||||||
|
|
construction d'images puissance vergence |
Quand un appareil optique donne une image réelle A'B' d'un
objet AB, on caractérise le couple " image objet" par le grandissement
: Quand l'image d'un objet réel est rejetée à l'infini, on ne
peut plus parler de grandissement. On défini l'angle a' (radian) sous lequel l'observateur voit
l'image et on définit la puissance de l'appareil par la relation : Une telle situation est réalisée dans l'utilisation normale
d'un microscope. Le but de cet exercice est d'étudier cet appareil
modélisé par deux lentilles minces convergentes de vergences C1
et C2. On caractérise la distance entre les 2 lentilles par O1O2
( distance des centres optiques) ou par F'1F2 (
distance entr le foyer image de la lentille n°1 ( simulant l'objectif)
et le foyer objet de la lentille n°2 (simulant l'oculaire). Dans ce cas
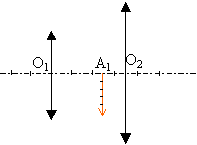
la puissance du microscope est donnée par : données : C1 =10d; C2= 5d. L'objet AB est une grille millimétrique transparente; l'image donnée par l'oculaire est notée A1B1 située dans le plan focal objet de L2. étude de l'objectif :
étude de l'oculaire :
étude du microscope modélisé :
|
|||||||||||||||||||||||||||||||||||||
| |
Chercher à obtenir l'image de ce tube néon sur la table. Mesurer au double décimètre la distance lentille-table.
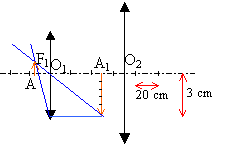
taille objet : environ le quart de AB; position AO1 voisin de 15 cm. grandissement : 0,5 / (-0,15 ) voisin de -3,5 l'image est réelle, plus grande que l'objet et renversée par rapport à l'objet. une image réelle peut être observée sur un écran. A1 est au foyer principal objet de L2 d'après le texte, l'image définitive est donc à l'infini.
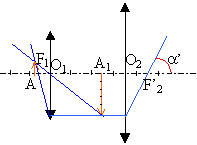
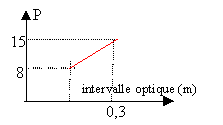
Le graphe est une droite (passant par l'origine): cette droite traduit la proportionnalité entre la puissance et l'intervalle optique. Son coefficient directeur est : (15-8) / 0,3-0,15 ) =46,6, valeur voisne du produit C1C2 ( 10*5 = 50). Le tableau indique que la puissance augmente lorsque la distance objet - objectif diminue. On approche l'objet de l'objectif. P= 100*40*0,17 = 680 m-1 ou dioptries a' = 680 * 10-5 = 6,8 10-3 rad. l'angle étant petit on peut confondre l'angle en radian avec sa tangente :
a =tan a = 10-5 / 0,25 = 4 10-6 rad impossible d'observer à l'oeil nu. |
||||||||||||||||||||||||||||||||||||||
|
|
|