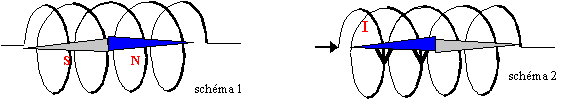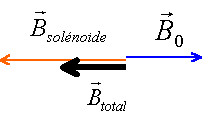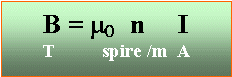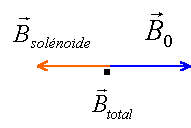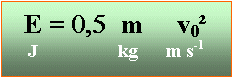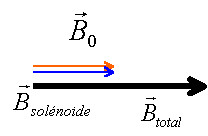
Aurélie sept 2000


devoirs en terminale S

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1

champ magnétique

d'un solénoïde

Soit un solénoïde très long comportant n=500 spires m-1 dont l'axe est situé dans le plan du méridien magnétique terrestre . On place dans la région centrale du solénoïde l' aiguille d'une boussole. En l'absence de courant dans le solénoïde ,l'aiguille s'oriente sur l'axe dans le sens de la composante horizontale du champ magnétique terrestre B0 .(schéma n°1)

Quand on établi un courant d'intensité I suffisamment élevé , l'aiguille de la boussole tourne de 180° .

Données :perméabilité du vide m0= 4 p 10 -7 S.I B0=2 10-5 T p² =10

Répondre par vrai ou faux en justifiant :

  1. Le courant I qui traverse le solénoïde a le sens indiqué sur le schéma 2 .
  2. Si le champ magnétique crée par le solénoïde vaut 2 B0 l'intensité du courant I vaut environ 60 mA.
  3. Lorsque le solénoïde est parcouru par un courant I2 = 0,5 I ,l'aiguille tourne de 90°.
  4. On garde I2= 0,5 I mais on inverse le sens du courant dans la bobine : la valeur du champ magnétique total auquel est soumise l'aiguille aimantée est alors 2 B0.
corrigé
.
.

En l'absence de courant dans la bobine, la boussole s'oriente suivant la composante horizontale du champ magnétique terrestre, horizontale à droite.

En présence du courant la boussole s'oriente suivant le champ total crée par la terre et par la bobine. Ce champ total est horizontal vers la gauche.

La régle de l'observateur d'Ampère donne le sens du courant I

champ uniforme crée par le solénoïde dans la partie centrale de la bobine

B=4*3,14 10-7*500*0,06 =3,8 10-5 T

c'est à dire environ deux fois la composante horizontale du champ terrestre

Si l'intensité du courant est divisée par 2, alors le champ du solénoïde est divisé par 2 et vaut seulement B0

Le champ résultant étant nul, la boussole reste immobile dans la position où on la placera. Mais elle ne tourne pas.

Inverser le sens du courant c'est inversé le sens du champ du solénoïde

 

2

conservation de l'énergie mécanique

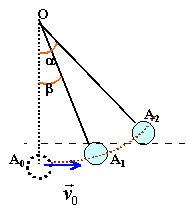Masse de la sphère m= 100g ;masse du fil négligé OA0=OA1= L = 50 cm

Point de départ A0 . Les frottements sont négligés. Origine des altitudes A0 . vitesse initiale 7,2 km h-1

  1. Exprimer l'énergie potentielle en A1 en fonction de g, m ,L b.
  2. Calculer l'énergie mécanique .
  3. Calculer a , A2 étant l'altitude maximale atteinte.
  4. En A2 ,la résultante des forces appliquées à la sphère est t'elle nulle.

corrigé



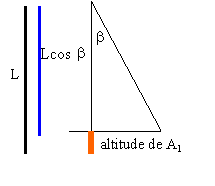
altitude de A1 = L (1-cos b)

énergie potentielle en A1 (l'origine est prise en A0.)

m g L (1-cos b)

L'énergie mécanique étant constante il suffit de la calculer en A0. En ce point l'énergie potentielle étant nulle, l'énergie mécanique est sous forme cinétique.

 

7,2 km h-1 = 7,2 / 3,6 = 2 m s-1.

0,5*0,1*2² = 0,2 J

En A2 l'énergie est sous forme potentielle de pesanteur, la bille s'arrête avant de rebrousser chemin.

m g L(1-cos a) = 0,2

(1-cos a) = 0,2 / (0,1* 9,8*0,5)= 0,408

cos a = 1-0,408 =0,592

a = 53,7 °


3

acide fort

base forte
  1. On ajoute 1 g de fer à 500 mL d'une solution d'acide chlorhydrique de pH=1. Quel est le pH après réaction ?
Fe2+ /Fe -0,44 V H3O+ /H2 = 0 V masse atomique molaire en g mol-1 Fe=56

2 On mélange 10 mL de soude de pH = 12 à 10 mL de potasse de pH=13.

Quel est le pH du mélange ?

corrigé



équation bilan

Fe + 2H3O+ --> Fe2+ + H2 + 2H2O

Quantité de matière initiale des réactifs :

fer :1 /56 = 0,0178 mol

ion hydronium : pH=1 donc

0,1 mol dans 1 L ou 0,05 mol dans 0,5 L

0,0178 mol de fer sont attaquées par 2*0,0178 = 0,0357 mol d'ion hydronium

L'acide est donc en excès de : 0,05 -0,0357= 0,0143 mol

0,0143 mol d'ion hydronium dans 0,5 L

soit 0,0143/0,5 =0,0286 mol L-1.

pH= -log(0,0286) = 1,54

il faut travailler avec les ions majoritaires soit les ions hydroxdes en solution basique. On recherche la quantité d'ion hydroxyde dans le mélange.

soude et potasse sont des bases fortes

  • pH=12 donc [HO-]= 10-2 mol L-1.
soit 10-4 mol d'ion HO- dans 10 mL
  • pH=13 donc [HO-]= 10-1 mol L-1.
soit 10-3 mol d'ion HO- dans 10 mL
  • total : 1,1 10-3 mol d'ion HO- dans 20 mL
[HO-]= 1,1 10-3 / 0,02 = 0,055 mol L-1.
  • [H3O+] = 10-14 /0,055 = 1,82 10-13 mol L-1.
pH= -log(1,82 10-13) = 12,7





retour - menu
à suivre