|
.
. |
complexes , puissance, Thévenin, Fresnel En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
modèle de Thevenin puissances |
On considère le montage suivant : V=10 V; R1=5W; 1/(Cw)=2W; R2=3W; Lw=5W; f=1 kHz. 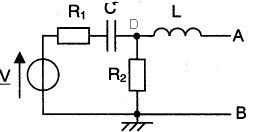
corrigé |
|
|
|
on peut leurs appliquer les lois du courant continu modèle de Thévenin : calcul de Zth supprimer la source de tension impédance de la brance {R1 C} : Z1= R1-j /(Cw) = 5-2j Z1 en dérivation avec R2 : impédance de l'ensemble Z2 = R2Z1/(R2+Z1)=3(5-2j) / (5-2j+3) Z2 = (132-18j) /68 =1,941-0,265j Z2 en série avec L : impédance Zth : Z2+jLw= 3(5-2j) / (8-2j) +5j Zth =1,941+4,735j. soit Z²th = (1,941²+4,753²) et Zth =5,11 W. j1 = tan-1(4,753 / 1,941)= 67,8°. calcul de ETh = UAB (circuit ouvert) = UDB. pas de courant dans L en circuit ouvert. UDB=R2i =V-Z1 i d'où i = V/(Z1+R2) 10/(8-2j)= 5/17(4+j)=1,176+0,294j. E th = R2i = R2V /(Z1+R2)=3*(1,176+0,294j) E th = 3,53 + 0,882j. soit E²th = (3,53²+0,882²) et Eth =3,64 W. j2 = tan-1(0,882 / 3,53)= 14°.
puissance active absorbée par Z : la puissance absorbée par Z est maximale lorqu'il y a adaptation d'impédance impédance Z = conjugué de l'impédance de la source R3= 1,941 W et jX3 = -4,735j. il s'agit d'un condensateur de capacité C associé à une résistance : w=2*3,14*100=6280 rad/s 1(Cw)=4,735 d'où C = 33,6 mF.
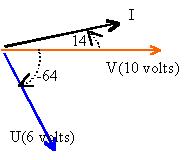
intensité, tension aux bornes de la charge Z, puissances: les impédances Z et Zth sont en série aux bornes de la source de f.e.m complexe Eth. Z et Zth = (1,941+ R3) + j (4,735 + X3) = 1,941+ R3. intensité dans Z : i = Eth / (Z+Zth)= Eth / (1,941+ R3) (1) tension aux bornes de Z : u = Z i = Z Eth / (Z+Zth)= Z Eth / (1,941+ R3) (2) u =(R3-4,735j)(3,53+0,882j) / (1,941+ R3) puissance complexe dans Z : ½ u i* puissance active = partie réelle de la puissance complexe puissance réactive = partie imaginaire de la puissance complexe application numérique : R3=1W. i = Eth / 2,941 = 1,2 +0,3j j3= tan-1(0,3 / 1,2)= 14° . I² = 0,3²+1,2² d'où I = 1,24 A u = 2,62 -5,38j j4= tan-1(-5,28 / 2,62)= -63,6° . U² = 2,62²+5,28² d'où U = 5,9 V puissance complexe : 0,5(2,62 -5,38j)(1,2 +0,3j) p = 2,36 -2,83j puissance active consommée : P = 2,36W puissance réactive stockée puis restituée : Q= - 2,83 VAR puissance apparente: S²=P²+Q² d'où S = 3,68 VA V origine des phases (1) donne arg i = arg Eth= 14° Z = 1-4,735j donc arg Z= tan-1(-4,735 / 1 ) = -78° (2) donne arg u = arg Eth + arg Z =14-78 = -64°.
|
|
|
impédance puissance Fresnel
|
On considère le montage suivant : Ueff = 220 V; R1=1W; 1/(Cw)=3W; R2=3W; L1w=1W; L2w=3W 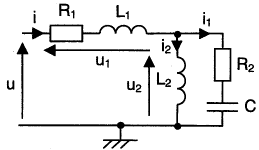
corrigé |
|
|
|
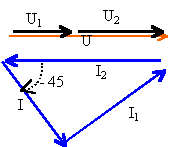
branche {L1 R1}: R1+jL1w = 1+j branche {R2 C} : R2-j/(Cw)=3-3j branche {L2 }: jL2w = 3j branche {R2 C} et branche {L2 }en dérivation : dipole équivalent aux deux branches en dérivation , impédance Z1 Z1 = 3j(3-3j) / (3j+3-3j) = j(3-3j) = 3+3j =3(1+j) Z1 en série avec branche {L1 R1}: d'où Z ensemble = 1+j +j(3-3j) = 4+4j remarque : les impédances Z1 et Z en série ont le même argument. impédance réelle : R=4W et dipole inductif Lw= 4W. module de Z : rac carrée(4²+4²)= 5,65 W. u =Z i ou arg u = arg Z+ arg i si argu = 0, origine des phases alors arg Z= -arg i arg Z= 4/4 = 1 d'où j = tan-1(1) = 45° intensité fournie par l'alimentation en retard 45 ° sur la tension. puissances : I eff = 220 / 5,65 d'où Ieff = 38,9 A puissance active : P = Ueff Ieff cos 45 = 220 *38,9*0,707 = 6 kW puissance réactive : Q = Ueff Ieff sin 45 = 6 kVAR autre méthode, à partir de la puissance complexe p =½ui* i = u / Z = u / (4+4j) = u(4-4j) / 32 = u / 8 (1-j) = 220*1,414/8 (1-j) = 38,9 (1-j) puissance complexe : 0,5 *220*,1414*38,9(1+j) = 6050(1+j) puissance active = partie réelle de p : 6 kW puissance réactive = partie imaginaire de p : 6 kVAR
intensité complexe dans chaque branche : branche {L1 R1}: intensité fournie par l'alimentation i = u / Z = u / (4+4j) = u(4-4j) / 32 = u / 8 (1-j) = 220*1,414/8 (1-j) = 38,9 (1-j) branche {R2 C} : impédance 3-3j intensité complexe i1 : u2 = (3-3j) i1 . branche {L2 }: impédance 3j intensité complexe i2 : u2 = 3j i2 . d'où une relation entre i1 et i2 : j i2 =(1-j) i1 soit i2 = -(1+j) i1. loi des noeuds : i = i1+ i2 = i1-(1+j) i1= -j i1soit i1 = j i et i2 =(1-j)i.
tension complexe u1 : u1 = (1+j) i = (1+j) *27,5 *(1-j) = 27,5 (1-j²) =55.
u2(t) = (220-55)*1,414 cos(wt) |