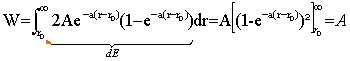|
.
. |
travail, puissance, énergie potentielle En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
potentiel de Morse potentiel de Yukawa |
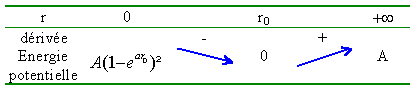
L'énergie potentielle d'interaction entre les atomes d'une molécule diatomique est donnée par l'expression du potentiel de Morse : E(r) =A(1-exp-a(r-r0) )². r : distance variable entre les atomes, a : constante positive, r0 et A : paramètres positifs dont il faudra déterminer la signification physique.
corrigé |
|
|
|
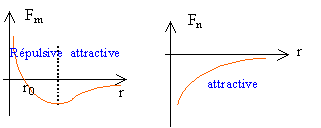
La force d'interaction moléculaire est conservative et dérive du potentiel E(r) Fm(r) = -dE / dr = -2Aa exp(-a(r-r0)) (1-exp(-a(r-r0))). il y a un équilibre lorsque cette force est nulle, c'est à dire lorsque r = r0. r0 représente la distance moyenne entre les deux atomes constituants la molécule. l'équilibre est-il stable ? -2Aa exp(-a(r-r0)) est négatif. si r>r0, -a(r-r0)<0 et (1-exp(-a(r-r0))) est posittif : Fm attractive. si r<r0, -a(r-r0)>0 et (1-exp(-a(r-r0))) est négatif : Fm répulsive. Fm est donc une force de rappel vers la position d'équilibre : celui ci est stable. l'énergie potentielle passe t-elle par un extrémum ? on dérive l'énergie potentielle : dE / dr = 2Aa exp(-a(r-r0)) (1-exp(-a(r-r0))) cette dérivée s'annule pour :1-exp(-a(r-r0))=0 soit r = r0
L'énergie potentielle passe par unminimum pour r= r0, ce qui correspond à un équilibre stable. énergie de dissociation travail fourni par un opérateur extérieur pour séparer les deux atomes constituant cette molécule dWop = -Fm dr
A représente l'énergie de dissociation de la molécule. Les forces d'interaction nucléaires sont conservatives et dérivent d'une énergie potentielle. Fn (r) = -dE / dr
les distances au niveau des molécules sont de l'ordre de 10-10m ; les distances au niveau du noyau sont de l'ordre de 10-15m. A court et moyen rayon d'action les forces nucléaires sont attractives, intenses lorsque les nucléons sont proches. Les forces moléculaires sont attractives ou répulsives
|
|
|
force attractive en 1/r² |
Soit une particule ponctuelle M de masse m gravitant
à la distance r =OM du centre d'un corps
sphérique; elle est soumise à une force
attractive :
corrigé |
|
|
|
La force ne dépend que de la variable r. Cette force dérive d'une énergie potentielle s'il existe une fonction E telle que f(r) = - dE/dr. ou bien dE = -f(r) dr : il suffit de rechercher une primitive de f(r) E=-K/r + Cte Lorsque la distance r devient très grande cette force et l'énergie potentielle n'existent plus, la constante est prise égale à zéro lorsque r tend vers l'infini. 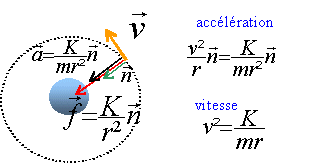
la vitesse a une norme constante: le mouvement est uniforme l'énergie cinétique vaut : Ec =½mv²=K/(2r). l'énergie mécanique est la somme des énergie potentielle et cinétique: E= -K/r+K/(2r) =-½ K/r dérivée logarithmique de l'expression de l'énergie dE/E = dr /r = -10-4. dérivée logaritmique de ll'expression de la vitesse : 2 dv/v = -dr/r dv/v = -½ dr/r = + 0,5 10-4 la vitesse augmente. arracher la particule de l'attraction du corps sphérique revient à lui fournir de l'énergie afin que son énergie totale devienne nulle. énergie apportée par l'opérateur : Eop = ½K/r0 énergie cinétique qu'il faut lui fournir ½mv² =½K/r0 d'où v²= K/(mr0) |